A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
23π2f2ml2
43f2ml2
4π2f2ml2
Zero
The correct Answer is:A
Step by step video, text & image solution for A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on rolling on incline plane)
28 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular momentum)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
A thin uniform rod of mass M and length l is rotating about a frictionless axis passing through one of its ends and perpendicular to the rod. The rod is heated uniformly to increases its temperature by Δθ. Calculate the percentage change in rotational kinetic energy of the rod. Explain why the answer is not zero. Take coefficient of linear expansion of the material of the rod to be α.
View SolutionA uniform rod of length l is given an impulse at right angles to its length as shown. Find the distance of instantaneous centre of rotation from the centre of the rod.
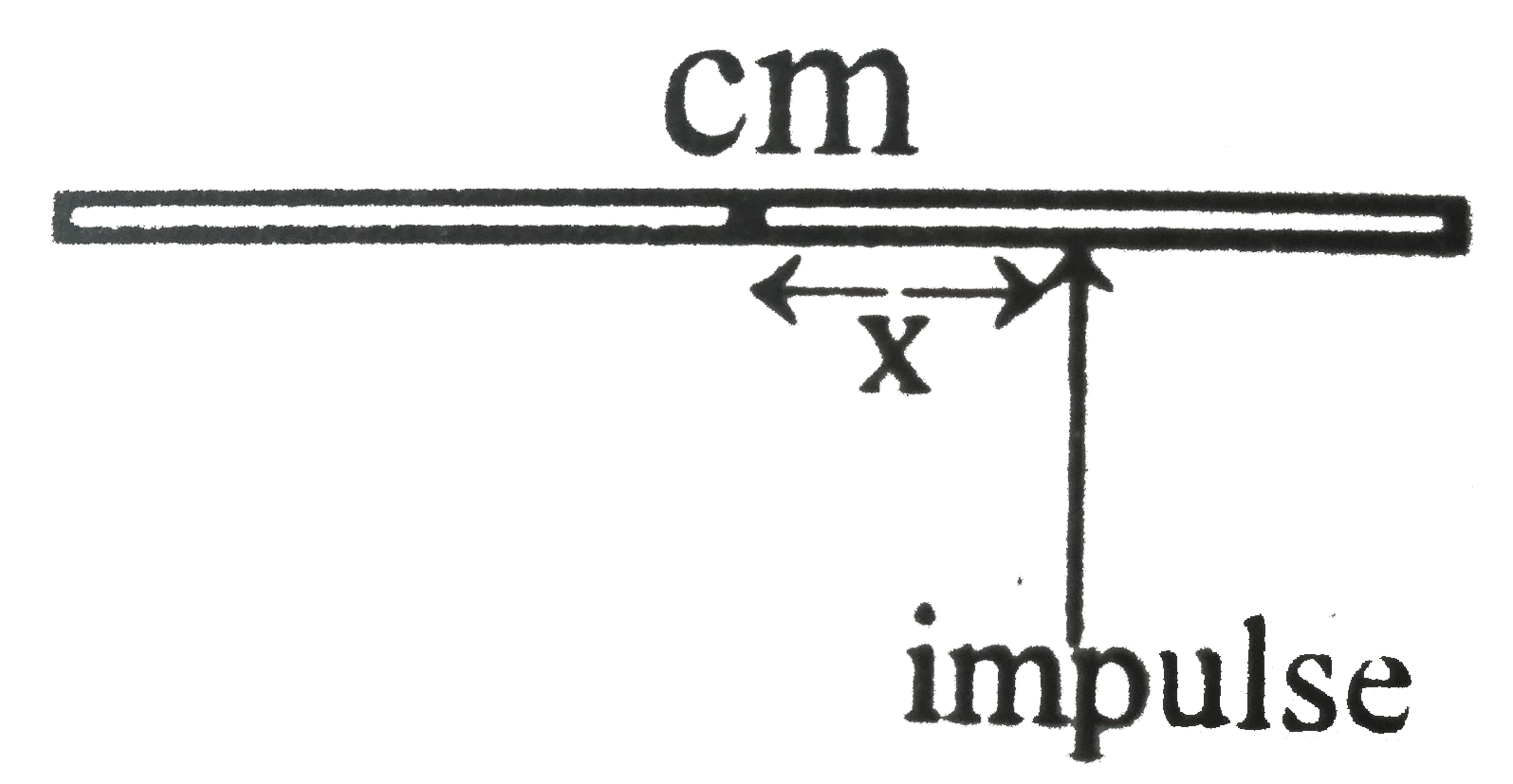 .
.
View Solution
Knowledge Check
A uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .A2√6g7lB√6g7lC2√3g7lD√3g7l
.A2√6g7lB√6g7lC2√3g7lD√3g7lUniform thin, rod AB of length L and mass m is undergoing fixed axis rotation whose axis of rotation passes through A, such that end A remains stationary as shown. The kinetic energy of section AP of rod is equal to kinetic energy of section BP of rod at a given instant. Then the ratio of length AP and length AB, that is, APAB is equal to
 A12B121/3C1√2D12√2
A12B121/3C1√2D12√2A uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is
 A49mL2ω224B2mω2L2C124mω2L2D13mL2ω224
A49mL2ω224B2mω2L2C124mω2L2D13mL2ω224
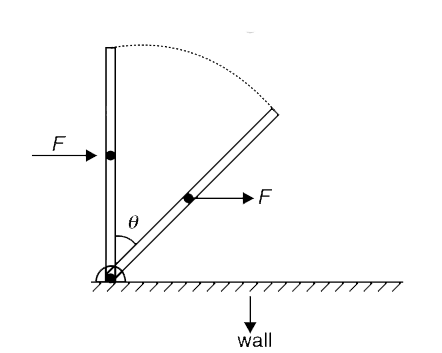
A uniform rod of mass M and length L is hinged at its end to a wall so that it can rotate freely in a horizontal plane. When the rod is perpendicular to the wall a constant force F starts acting at the centre of the rod in a horizontal direction perpendicular to the rod. The force remains parallel to its original direction and acts at the centre of the rod as the rod rotates. (Neglect gravity).
(a) With what angular speed will the rod hit the wall ?
(b) At what angle θ (see figure) the hinge force will make a 45∘ angle with the rod ?
View SolutionA rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
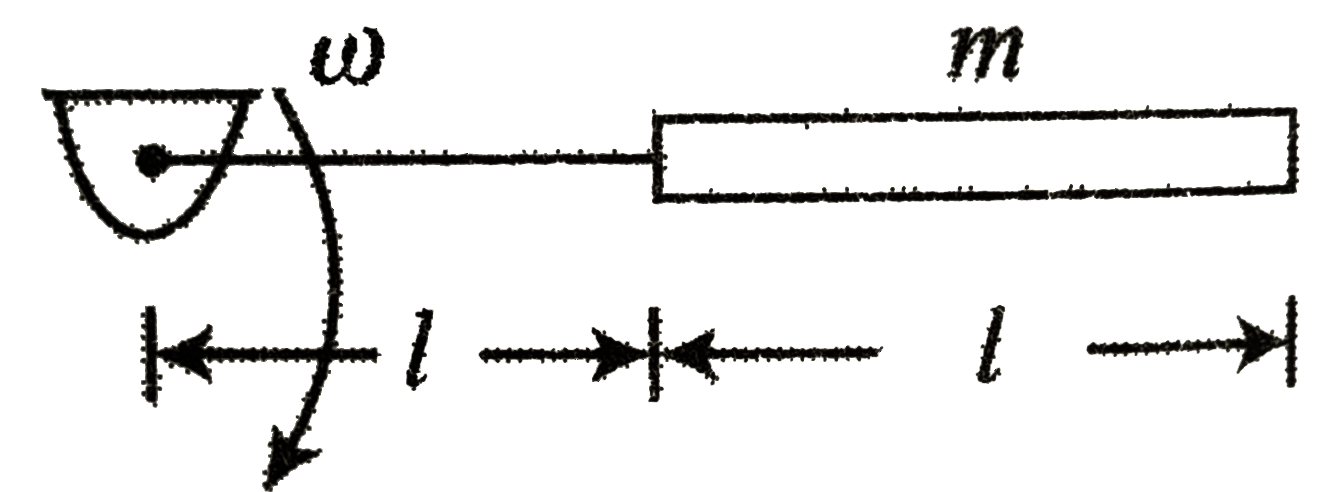
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View SolutionA rod of length l having uniformly distributed charge Q is rotated about one end with constant frequency f Its magnetic moment
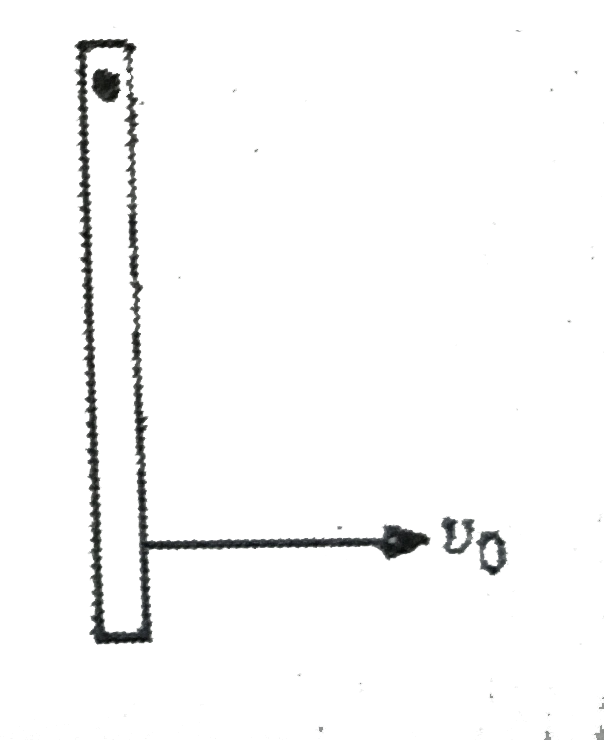
View SolutionA thin uniform rigid rod of length l is hinged at one end so that it can move ina vertical plane by rotating about a horizontal axis through upper end. The lower end is given a sharp blow and made to acquire a linear velocity Maximum height attained by lower end of the rod is:
View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View Solution
