A uniform tube of length 60 cm stands vertically with its lower end dipping into water. When the length above water successively taken at 14.8 cm and 48.0 cm, the tube responds to a vibrating tuning fork of frequency 512 Hz. Find the lowest fi-equency to which the tube will respond when it is open at both ends.
The correct Answer is:[283.30]
From the given resonating lengths we can use
48−14.8=(λ2)
λ = 66.4 cm.
Thus for given situaton wavelength is λ is λ = 64.4 cm so speed of sound is
v=nλ=512×0.664
= 339.97 m/s
Fundamental frequency of tube is
n0=v2l=399.972×0.6 = 283.30 Hz.
Topper's Solved these Questions
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.7
10 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.8
8 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.5
16 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
- X-RAYSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - X-RAYSEXERCISE - Unsolved Numerica Problem for Preparation
23 Videos
Similar Questions
A uniform tube of length 60cm stands vertically with its lower end dipping into water . First two air column lengths above water are 15cmand45cm, when the tube responds to a vibrating fork of frequency 500HZ . Find the lowest frequency to the tube will respond when it is open at both ends.
View SolutionSecond and third resonating length of resonace tube experiment were observed to be 54 cm and 89 cm when vibrated with a tuning fork of frequency 480 Hz. Find
Inner diameter of the tube
View Solution
Knowledge Check
A uniform tube of length 60.5 cm is held vertically with its lower end dipped in water. A sound source of frequency 500 Hz sends sound a waves into the tube. When the length of tube above water is 16cm and again when it is 50cm, the tube resonates with the source of sound . Two lowest frequencies to which tube will resonate when it is taken out of water are,
A281562B281843C276552D272544The length of pipe 4cm in diameter and open at both ends when it is set into vibrations by a tuning fork of frequency 288Hz. (v=332m/s)
A85.23cmB75.23cmC65.23cmD55.23cmIn reasonace tube experiment with a tuning fork of frequency 480Hz the consecutive reasonance lengths are 30cm then determine speed of sound is
A200m/sB256m/sC384m/sD240m/s
Second and third resonating length of resonace tube experiment were observed to be 54 cm and 89 cm when vibrated with a tuning fork of frequency 480 Hz. Find
Velocity of sound
View SolutionSecond and third resonating length of resonace tube experiment were observed to be 54 cm and 89 cm when vibrated with a tuning fork of frequency 480 Hz. Find
first resonating length
View Solution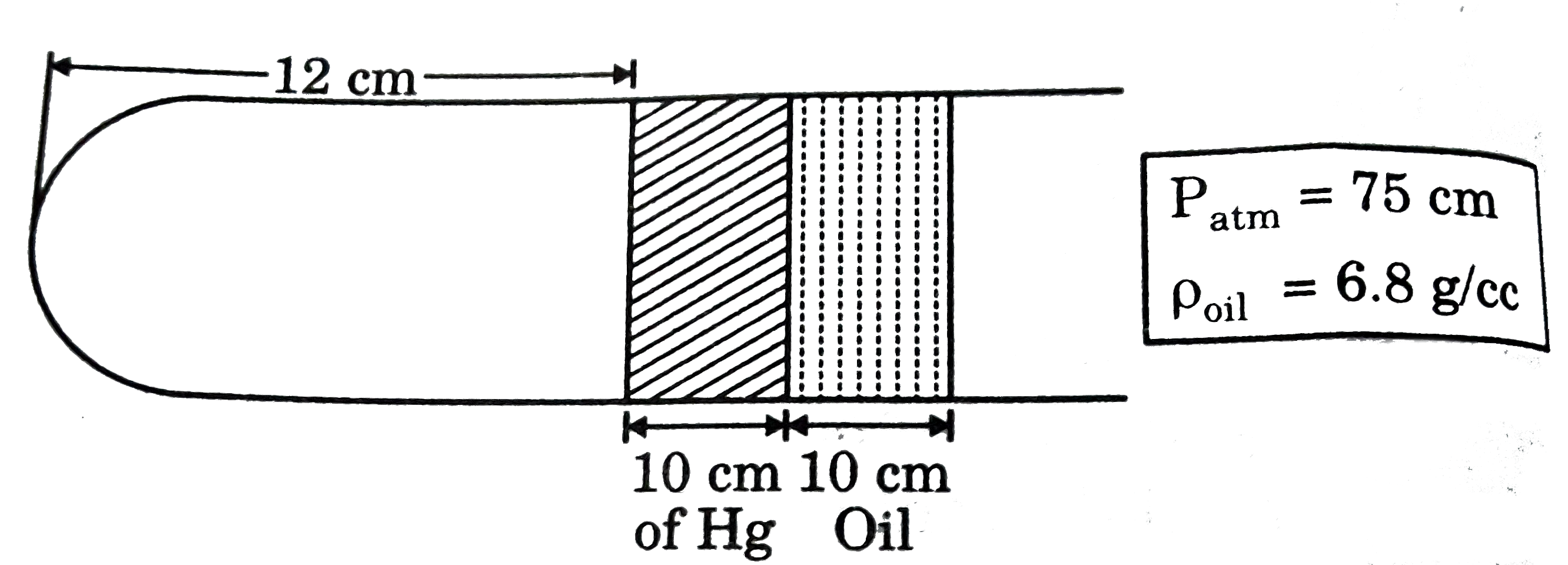
If above tube is held vertical with open end upward then find the length of air column (in cm).
View SolutionIn reasonace tube experiment with a tuning fork of frequency 480Hz the consecutive reasonance lengths are 30cm and 70cm then determine speed of sound is
View SolutionA capillary tube is kept vertical with the lower end dipped in water . The height of water raised in the capillary is 4 cm . If the length of the capillary tube is made 2 cm , then the angle made by the water surface in the capillary with the wall is
View Solution
