A uniform wire of resistance $12 Ω$ is cut into three pieces so that the ratio of the resistances $R_{1} : R_{2} : R_{3} = 1 : 2 : 3$ and the three pieces are connected to form a triangle across which a cell of emf 8V and internal resistance $1 Ω$ is connected as shown.

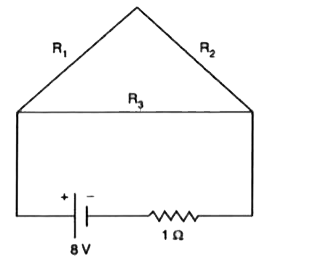
Calculate the current through each part of the circuit. Solution in Kannada

Video Solution

Text Solution

Verified by Experts

$R_{1} = 12 Ω$
$R_{1} : R_{2} : R_{3} = 1 : 2 : 3$
Let, $R_{1} = R R_{1} = 2 Ω$
$R_{2} = 2 R R_{2} = 4 Ω$
$R_{3} = 3 R R_{3} = 6 Ω$
According to circuit:
$\frac{(R_{1} + R_{2}) \times R_{3}}{R_{1} + R_{2} + R_{3}}$
$R_{e q} = 3 + 1 = 4 Ω$
$I = \frac{8}{4} = 2 A$
Current through each branch is 1 Ampere.

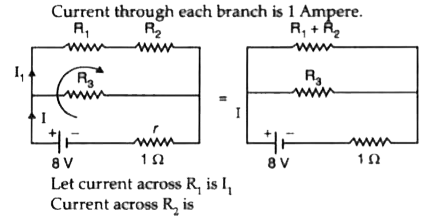
Let current across $R_{1} i s I_{1}$
Current across $R_{2}$ is
$I_{2} = I_{1}$
So current across
$R_{3} = I_{3} = (I - I_{1})$
Taking current dividing rule :
$I_{1} = \frac{R_{3}}{(R_{1} + R_{2} + R_{3})} \times I$
$= \frac{6}{(2 + 4 + 6)} \times 1 .$
$I_{2} = I_{1} = 1$ amp
$I_{3} = I - I_{1}$

= 1 amp

Updated on:21/07/2023

|

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

OSWAAL PUBLICATION-CURRENT ELECTRICITY -TOPIC-2 ( KIRCHHOFF.S LAWS & APPLICATIONS (NUMERICAL PROBLEMS)

Home
Ask Doubt
Profile