A uniiform disc of radius r spins with angular velocity ω and angular acceleration α. If the centre of mass of the disc has linear acceleration a, find the magnitude and direction of aceeleration of the point 1,2, and 3.

The acceleration of point 1:→a1=→a1,C+→aC
But →a1,C=(→a1,C)tangential+(→a1,C)radial

⇒→a1,C=αRˆj+ω2Rˆi and →aC=aˆi
Hence →a1=(ω2R+a)ˆi+αRˆj
Similarly the acceleration of 2:→a2=→a2,+→aC
Here →a2,C=(αRˆi−ω2Rˆj) and →aC=aˆi
Hence →a2=(a+αR)ˆi−ω2Rˆj
Also acceleration of 3, →a3=→a(3,c)=aˆi
Hence →a3=(a−ω2R)ˆi−αRˆj
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
The angular velocity and angular acceleration of the pivoted rod are given as ω and α respectively. Fid the x and y components of acceleration of B.
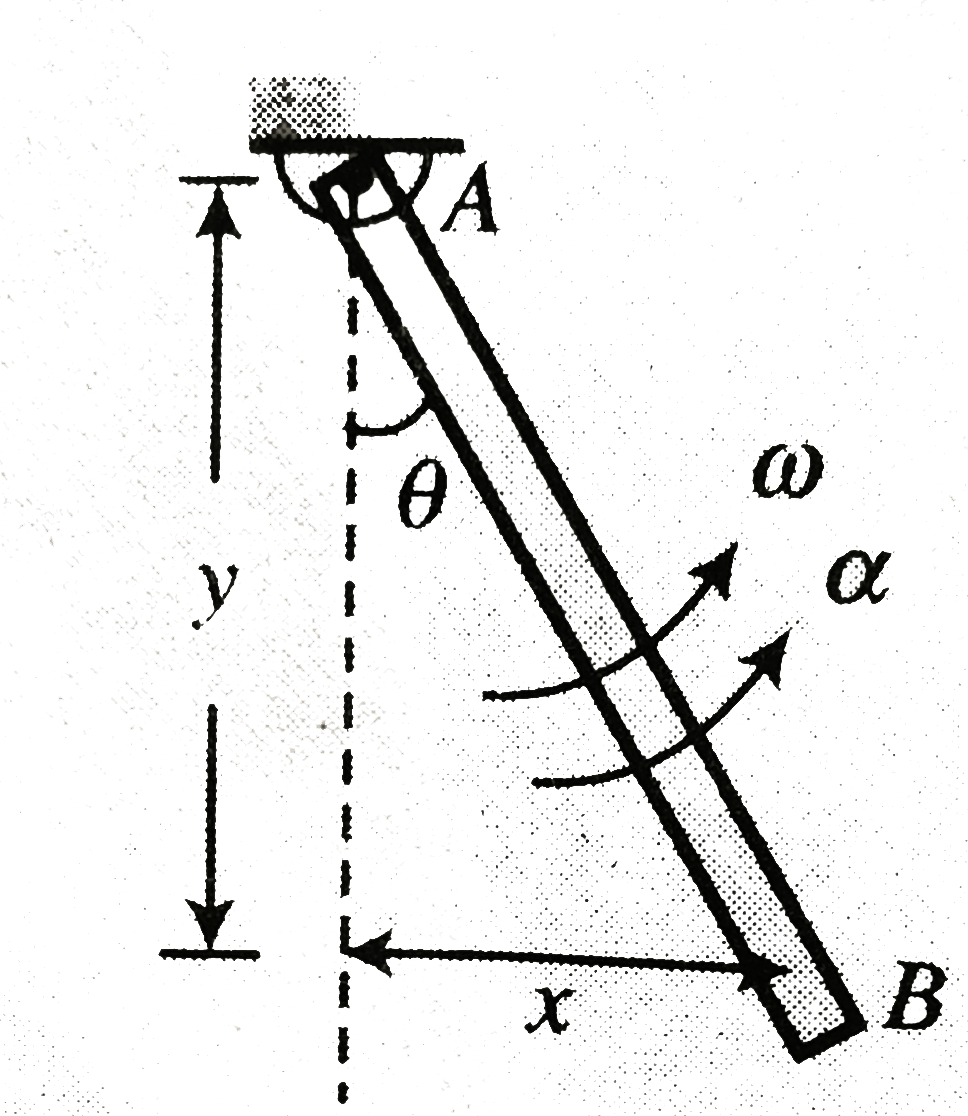
View SolutionA uniform disc of radius R=2√3m is moving on a horizontal surface without slipping. At some instant its angular velocity is ω=1 rad/s and angular acceleration is a α=√3rad/s2.

(a) Find acceleration of the top point A.
(b) Find acceleration of contact point B.
(c) Find co - oridnates (r,θ) for a point P which has zero acceleration
View Solution
Knowledge Check
A ball of radius r is rolling (pure rolling) on a convex stationary circular surface of radius R with angular velocity ω and angular acceleration α. The magnitude of vertical acceleration of top point of the ball is
Aω2r(R+2rR+r)Bω2rCω2rR+rDω2rRR+rIf angular velocity of a disc depends an angle rotated θ as ω=θ2+2θ, then its angular acceleration α at θ=1 rad is :
A8rad/s2B10rad/s2C12rad/s2DNone of theseA disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
A(1/2)MR2ωBMR2ωC(3/2)MR2ωD2MR2ω
A uniform disc of radius R is spinned to the angular velocity ω and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be neglected as uniform.
View SolutionA uniformly charged disc of radius r and having charge q rotates with constant angular velocity ω. The magnetic dipole moment of this disc is 1nqωr2. Find the value of n.
View SolutionA disc with linear velocity v and angular velocity ω is placed on rough ground. Suppose a and α be the magnitudes of linear and angular acceleration due to friction.
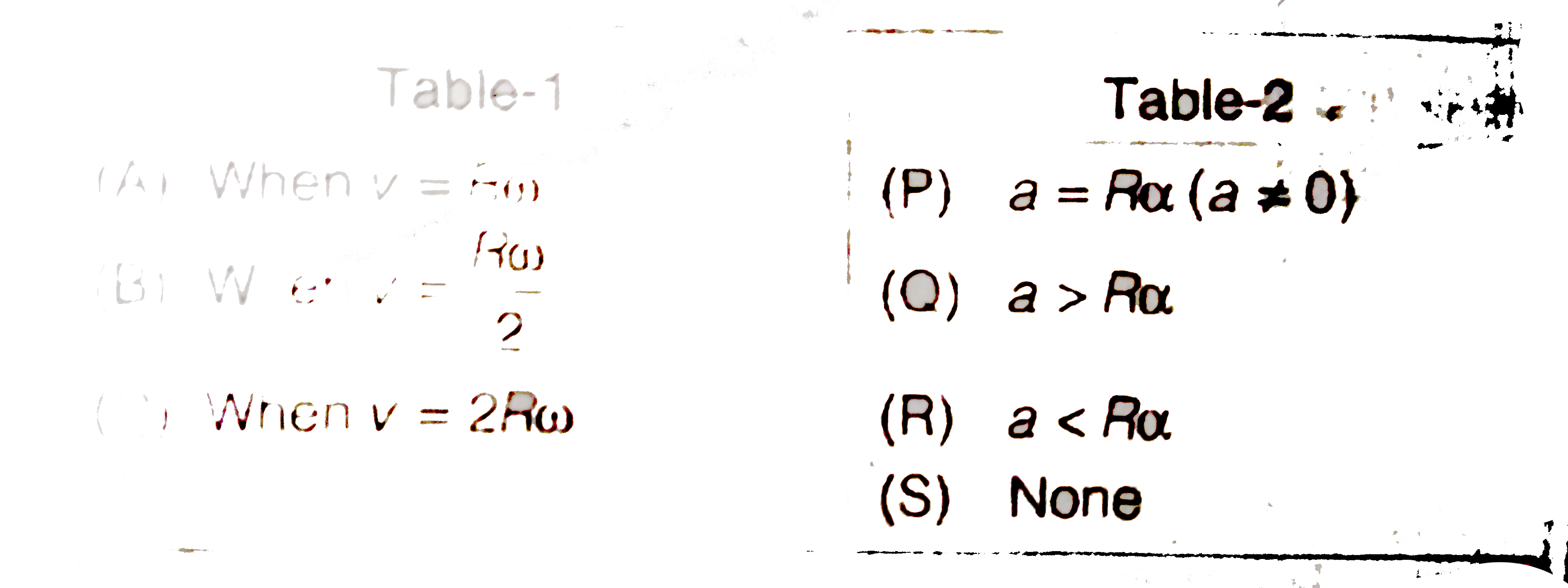

View SolutionA disc is rolling without slipping with angular velocity ω. P and Q are two points equidistant from the centre C. the order of magnitude fo velocity is

View Solution
A ring of radius R rolls on a horizontal surface with constant acceleration a of the centre of mass as shown in figure. If ω is the instantaneous angular velocity of the ring. Then the net acceleration of the point of contact of the ring with gound is
View Solution
