Question

(a) Using the necessary ray diagram, derive the mirror formula for a concave mirror.
(b) In the magnified image of a measuring scale (with equidistant markings) lying along the principal axis of a concave mirror, the markings are not equidistant. Explain.

Answer

a

Explanation

(a) Figure, shows ray diagram explaining formation of a real image of a linear object AB placed in front of a concave mirror MPN of focal length f Since aperture of mirror is small, hence MP be considered to be a straight line.
Let us consider right angled triangles A.B.F and MPF, which are similar triangles. Therefore,
`(B.A.)/(PM)=(B.F)/(FP)`
But as PM= AB, hence, we have
`(B.A.)/(BA)=(B.F)/(FP)` ....(i)
Again triangles APB and A.PB. are also similar triangles and we have
`(B.A.)/(BA)=(B.P)/(BP)`

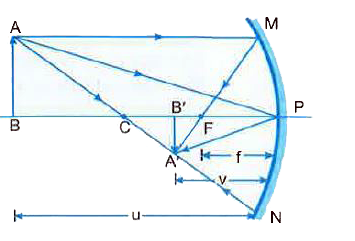
Comparing (i) and (ii), we get `(B.P)/(BP)=(B.F)/(FP)=(B.P-FP)/(FP)`
As per sign convention followed: BP = -u, B.P =-v, and FP =-f Therefore, we get
`((-v))/((-u))=((-v)-(-f))/((-f))rArrv/u=(v-f)/f`
`rArrvf=uv-uf` or `uf+vf=uv`
Dividing throughout by uvf, we get
`1/v+1/u=1/f`, which is the requisite mirror formula.
(b) Magnification of a mirror is given as:
`m=-v/u=f/(f-u)`
As different markings of a measuring scale lying along the principal axis of a concave mirror are at different positions (i.e., u is different for them), we get magnified images of these marks but magnification differs from one mark to another. As a result, the markings in image are not equidistant.