A valley has two walls inclined at 37° and 53° to the horizontal. A particle is projected from point P with a velocity of u=20m/s along a direction perpendicular to the incline wall OA. The Particle hits the incline surface RB perpendicularly at Q. Take g=10m/s2 and find:
(a) The time of flight of the particle.
(b) Vertical height h of the point P from horizontal surface OR.
[tan37∘=34]
![A valley has two walls inclined at 37° and 53° to the horizontal. A particle is projected from point P with a velocity of u = 20 m//s along a direction perpendicular to the incline wall OA. The Particle hits the incline surface RB perpendicularly at Q. Take g = 10 m//s^(2) and find: (a) The time of flight of the particle. (b) Vertical height h of the point P from horizontal surface OR. [tan 37^(@) = (3)/(4)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C02_E01_118_Q01.png)
The correct Answer is:(a) 2.5s (b) 4.05m
Topper's Solved these Questions
Similar Questions
Two inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
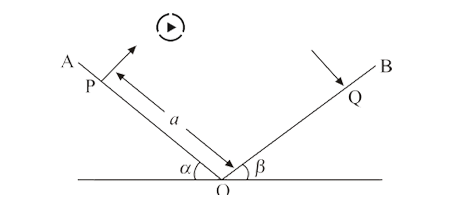
The path of the particle from P to Q is
View SolutionTwo inclined planes OA and OB having inclinations 30∘ and 60∘ with the horizontal respectively intersect each other at O, as shown in figure. A particle is projected from point P with velocity u=10√3m/s along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular at Q. Calculate.
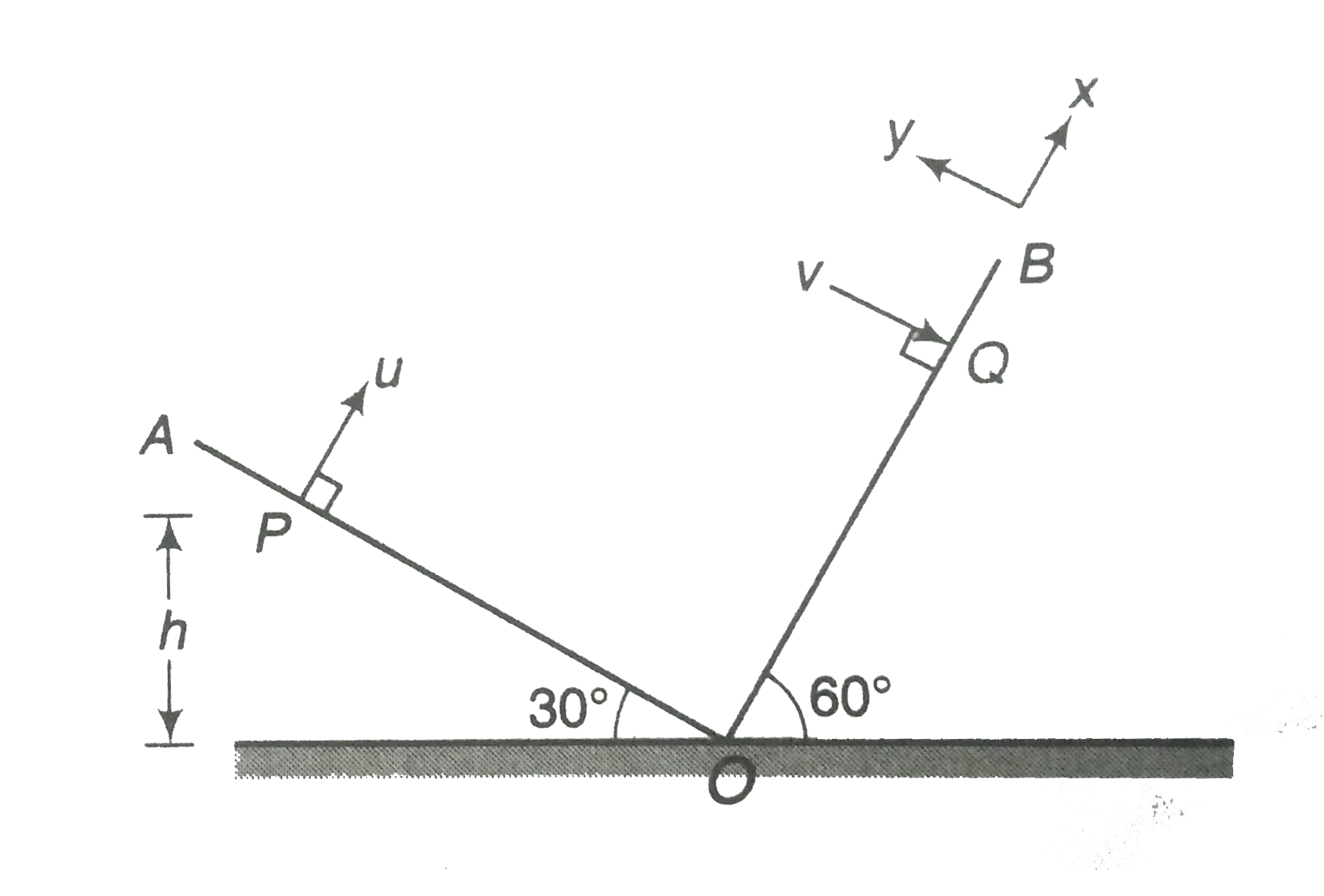
(a) time of flight,
(b) velocity with which the particle strikes the plane OB,
(c) height h of point P from point O,
(d) distance PQ. (Take g=10m/s2)
View Solution
Knowledge Check
Two inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘ respectively , intersect each other at O. A particle is projected from point 'P' with velocity u=10√3 m/s along a direction perpendicu lar to plane OA. If the particle strikes plane OB perpendicu lar at Q. Calcu late:

Time of flight of the particle:A8sB6sC4sD2sTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.

The path of the particle from P to Q isArectilinearBcircularCparabolicDellipticalTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
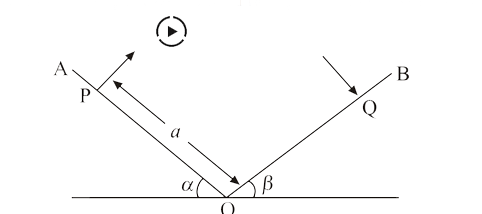
If α=30∘,β=30∘ the time of flight from P to Q isAugB√3ugC√2ugD2ug
Two inclined planes OA and OB having inclinations 30∘ and 60∘ with the horizontal respectively intersect each other at O, as shown in figure. A particle is projected from point P with velocity u=10√3m/s along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular at Q. Calculate.

(a) time of flight,
(b) velocity with which the particle strikes the plane OB,
(c) height h of point P from point O,
(d) distance PQ. (Take g=10m/s2)
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.

If α=30∘,β=30∘ the time of flight from P to Q is
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.

If α=30∘,β=30∘ the time of flight from P to Q is
View SolutionA particle is projected horizontally with speed u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g =10m/s2]
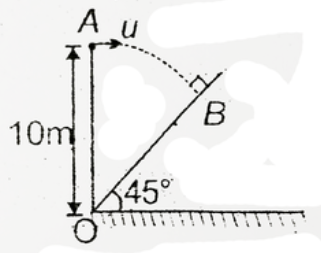
Find horizontal speed with which the particle was projected
View SolutionA particle is projected with a velocity of 20 m/s at an angle of 30∘ to an inclined plane of inclination 30∘ to the horizontal. The particle hits the inclined plane at an angle 30∘, during its journey. The time of flight is -
View Solution
