A vertical cylinder of height 100 cm contains air at a constant temperature and its top is closed by a frictionless piston at atmospheric pressure (76 cm of Hg) asshown in figure-2.12. If mercury is slowly poured on the piston, due to its weight airis compressed. Find the maximum height of the mercury column which can be put on the piston.
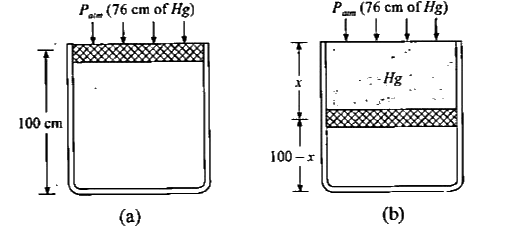
When mercury is poured on the top of the piston, due to increase in pressure, the volume of air will decrease according to Boyle's
Law. If final mercury column of height x is poured on the piston than gas pressure in equilibrium can be given as
Pf=(76+x) cm of Hg
As atmospheric pressure is equivalent to the pressure due to a mercury column of height 76 cm. If A be the area of cross section of cylinder then we have according to Boyle's Law
P1V1=P2V2
or (76 cm)(100 A)=(76+x)(100−x)A
or 7600=7600+24x−x2
or x=24 cm
Topper's Solved these Questions
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Discussion Question
18 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Conceptual MCQs Single Option Correct
27 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
66 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - U.N.P
79 Videos
Similar Questions
A vertical cylinder of height 100cm contains air at a constant temperature. The top is closed by a friction less light piston. The atmospheric pressure is equal to 75 cm of mercury. Mercury is slowly poured over the piston. Find the maximum height of the mercury column that can be put on the piston.
View SolutionFigure shows a cylindrical container containing oxyegn (γ=1.4) and closed by a 50 kg frictionless piston. The area of cross section is 100cm(2) , atmospheric pressure is 100kPa+E2 and g is 10 m s^(-2). The cylinder is slowly heated for some time. Find the amount of heat supplied to gas if the piston moves out through a distsnce of 20 cm.
 .
.
View Solution
Knowledge Check
The arms of a U shaped tube are vertical. The arm on right side is closed and other arm is closed by light movable piston. There is mercury in the tube and initially the level of the mercury in the arms is the same. Above the mercury, there is an air column of height h in each arm, and initial pressure is the same as atmospheric pressure in both arms. Now pistion is slowly pushed down by a distance of h/2 (see figure)
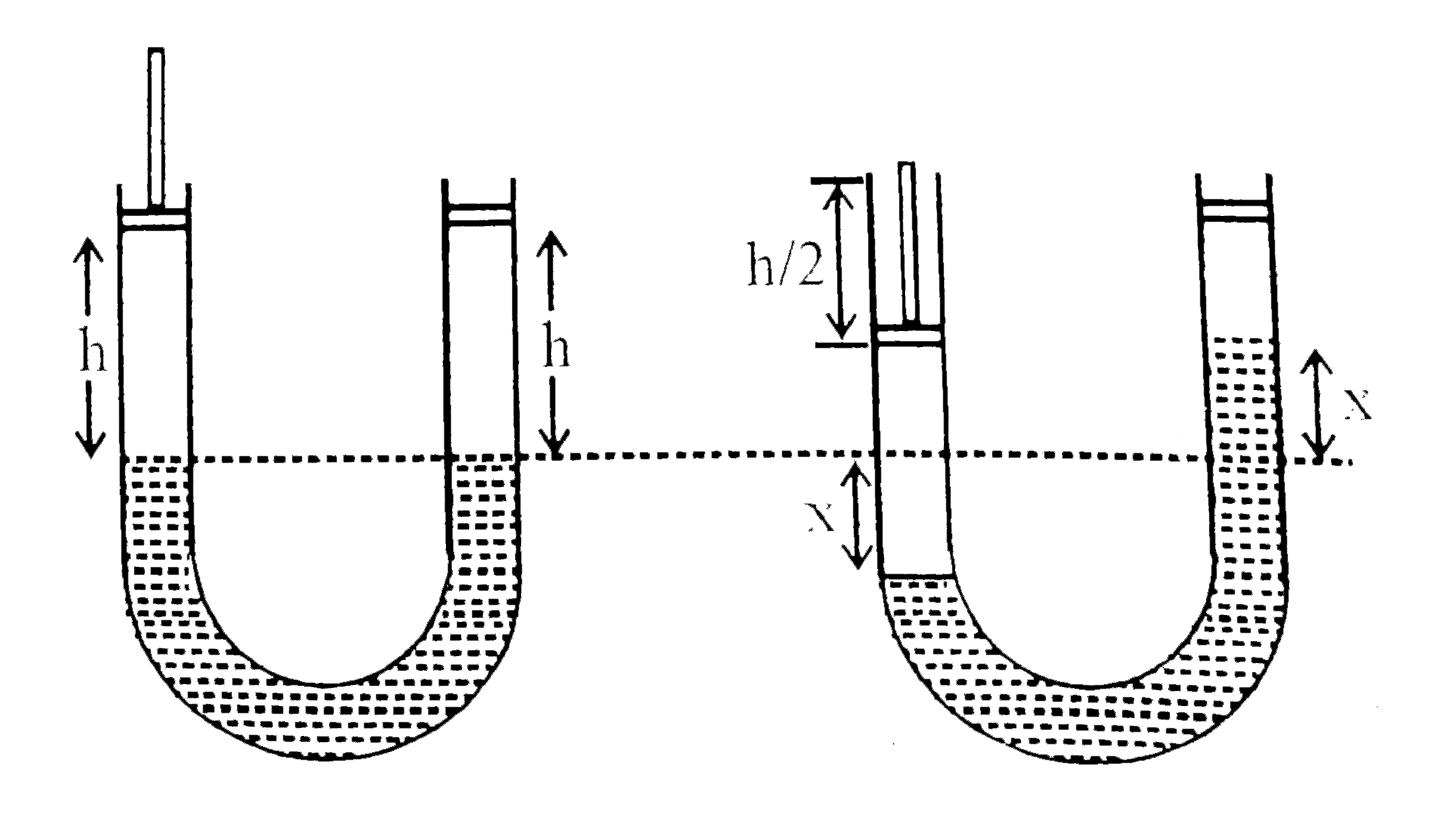
Let x is the displacement of mercury level in one of the stem and P1 is pressure in left column of air after compression, P2 is pressure in right column of air after compression and P0 is atmospheric pressure thenAhP0=(h2+x)P1BhP0=(h−x)P2CP1=P2DP1−P2=2xpg where p is density of mercuryFigure shows initial state of an ideal gas trapped in a container with conducting walls and a piston (mass m) which can move without any friction. The container is placed on point supports and its wall are conducting. Assuming that atmospheric pressure is P0 and the mass of the ideal gas is negligible as compared to the mass of the piston and the mass of container. Take the cross section area of piston to be A. The piston is slowly lifted by an external agent and held in its position. Let M be the maximum mass of container so that it may "lift off" while pulling the piston upwards and Pi be the pressure of ideal gas in initial state. Pick the correct choice:
 APi=P0+mgABPi=P02+mg2ACM=m2DM=P0A2g−m2
APi=P0+mgABPi=P02+mg2ACM=m2DM=P0A2g−m2A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
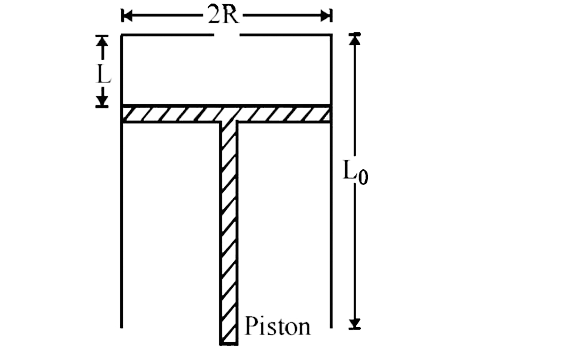
The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then beAP0BP02CP02+MgπR2DP02−MgπR2
A vertical cylinder of total length 100 cm is closed at the lower end and is fitted with a movable frictionless gas tight disc at the other end. An ideal gas is trapped under the disc. Initially the height of the gas column is 90 cm when the disc is in equilibrium between the gas and the atmosphere. Mercury is than slowly poured on the top of the disc and it just starts overflowing when the disc has descended through 32 cm. Find the atmospheric pressure (in cm of Hg). Assume that the temperature of the gas to remain constant and neglect the thickness and weight of the disc. Give your answer excluding the decimal places.

View SolutionA freely sliding massive piston is supported by a spring inside a vertical cylinder as shown. When all air is pumped out of the container, the piston remains in equilibrium with only a tiny gap between the piston and the bottom surface of the cylinder. An ideal gas at temperature T0 is slowly injected under the piston so that it rises to height h0 (see figure). Calculate the height of the piston from the bottom of the container if the temperature of the gas is slowly raised to 4T0.
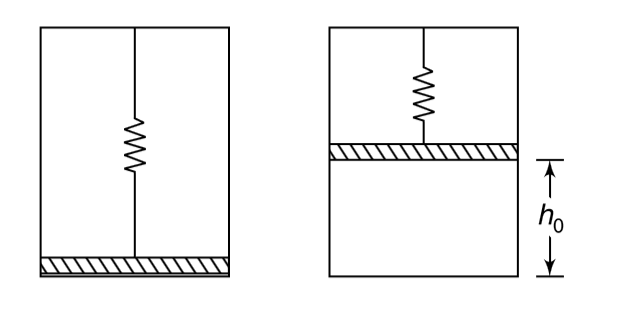
View SolutionA vertical cylinder of total lwgth 100 cm is closed at the lower end and fitted with a movable , frictionless, gas - tight disc ,at the other end. An ideal gas is trapped under the disc of negligible mass. Initially the height of the gas column is 90 cm and the dis is in equlibrium . Mercury is slowly poured on the top of the disc and it just starts overflowing when the disc has descended thorugh 32 cm. find the atmospheric pressure.
View SolutionA barometer tube contains a mixture of air and saturated water vopour in the space above the mercury column. It reads 70cm when the actual atmospheric pressure is 76cm of mercury. The saturation vapour pressure at roon tempature is1.0 cm of mercury, The tube is now lowered in the reservoir till the space above the mercury cloumn is reduced to half its origina volume. Find the reading of the barometer. Assume that the temperature remains constant.
View SolutionA fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
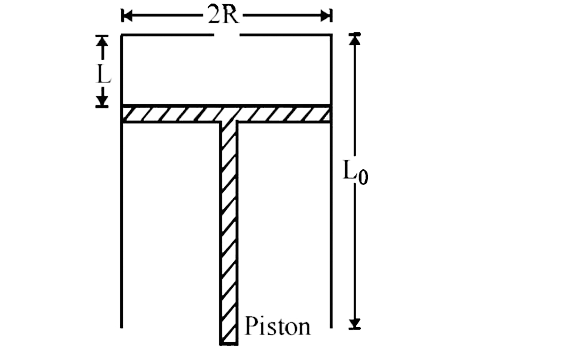
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
View Solution
