A vertically oriented uniform rod of mass and length can rotate about its upper end. A horizontally flying bullet of mass strikes the lower end of the rod and gets stuck in it as a result the rod swings through an angle . Assuming that . find
a. the velocity of the flying bullet:
b. the moment change in the system bullet rod during the impact: what causes that change of momentum.
The impulse acting on the rod -bullet system during the impact is shown in figure. is the impulse acting on the rod by the hinge. Here the role of is a little intersecting force. could be greater than zero could be equal to zero, , and could be less than zero . And as a consequence the linear momentum of the system may increase, may remain constant or may decrease.

a. During the impact, the moment ofimpulse acting o the rod bullet system ahout the hinge is zero. Angular momentum about the hine will remain constant. Let be the angular velocity of the system about the hinge.
......i
Where is the moment of inertia of the rod bullet system after collision about
.....ii
..............iii
As the system swings about hinge, the mechanical energy of the system will remain constant
From eqn iii ............iv
Substituting this value of in eqn we get
Now for
Thus
b. Change in linear momentum during the impact
.........v
From eqn iv and i
what causes linear momentum to change? Obviously, impulse at hinge. Here is positive, linear momentum increase so must be towards the right.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 View Solution
View SolutionA rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod
 View Solution
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
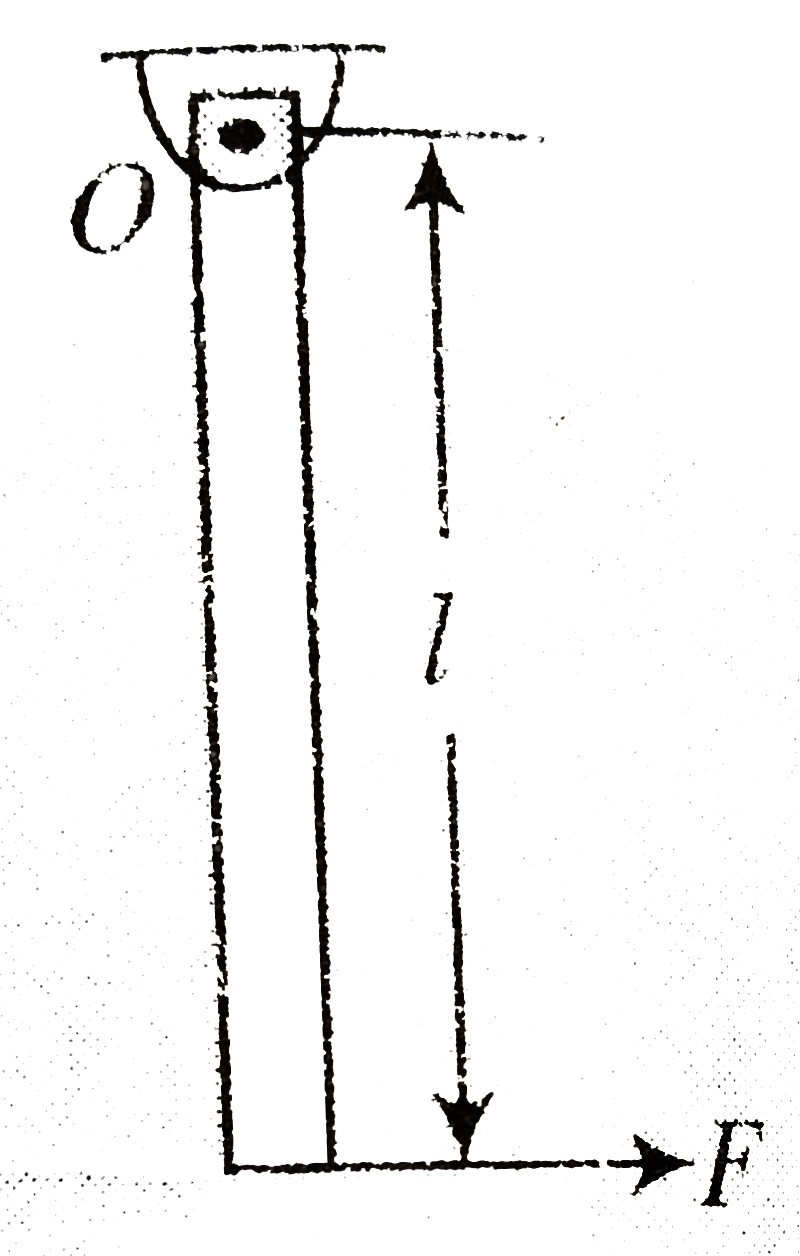 View Solution
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionA uniform rod of mass m and length L is hinged about one end and can freely rotate in a vertical plane. The angular velocity of the rod, when it falls from position P to Q. through an angle α starting from rest, is
 View Solution
View SolutionA uniform rod is resting freely over a smooth horizontal plane. A particle moving horizontally strikes at one end of the rod normally and gets stuck. Then
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 View Solution
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 View Solution
View Solution
