A voltmeter of resistance 998Ω is connected across a cell of emf 2 V and internal resistance 2Ω. Find the p.d. across the voltmeter, that across the terminals of the cell and percentage error in the reading of the voltmeter.
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- EMF of the cell (E) = 2 V
- Internal resistance of the cell (r) = 2 Ω
- Resistance of the voltmeter (R) = 998 Ω
Step 2: Calculate the total resistance in the circuit
The total resistance in the circuit is the sum of the internal resistance of the cell and the resistance of the voltmeter:
Rtotal=r+R=2Ω+998Ω=1000Ω
Step 3: Calculate the current flowing through the circuit
Using Ohm's law, the current (I) flowing through the circuit can be calculated as:
I=ERtotal=2V1000Ω=0.002A(or2×10−3A)
Step 4: Calculate the potential difference across the voltmeter
The potential difference (V) across the voltmeter can be calculated using Ohm's law:
V=I×R=0.002A×998Ω=1.996V
Step 5: Calculate the potential difference across the terminals of the cell
The potential difference across the terminals of the cell is equal to the voltage across the voltmeter since they are connected in parallel:
Vterminal=V=1.996V
Step 6: Calculate the percentage error in the reading of the voltmeter
The percentage error can be calculated using the formula:
Percentage Error=E−VE×100
Substituting the values:
Percentage Error=2V−1.996V2V×100=0.004V2V×100=0.2%
Summary of Results
- Potential difference across the voltmeter: 1.996 V
- Potential difference across the terminals of the cell: 1.996 V
- Percentage error in the reading of the voltmeter: 0.2%
- EMF of the cell (E) = 2 V
- Internal resistance of the cell (r) = 2 Ω
- Resistance of the voltmeter (R) = 998 Ω
The total resistance in the circuit is the sum of the internal resistance of the cell and the resistance of the voltmeter:
Rtotal=r+R=2Ω+998Ω=1000Ω
Using Ohm's law, the current (I) flowing through the circuit can be calculated as:
I=ERtotal=2V1000Ω=0.002A(or2×10−3A)
The potential difference (V) across the voltmeter can be calculated using Ohm's law:
V=I×R=0.002A×998Ω=1.996V
The potential difference across the terminals of the cell is equal to the voltage across the voltmeter since they are connected in parallel:
Vterminal=V=1.996V
The percentage error can be calculated using the formula:
Percentage Error=E−VE×100
Substituting the values:
Percentage Error=2V−1.996V2V×100=0.004V2V×100=0.2%
- Potential difference across the voltmeter: 1.996 V
- Potential difference across the terminals of the cell: 1.996 V
- Percentage error in the reading of the voltmeter: 0.2%
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems From Competitive
18 Videos
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems For Self
101 Videos
- CHEMICAL EFFECT OF CURRENTBOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B
5 Videos
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problems for self practive
61 Videos
Similar Questions
A voltmeter of resistance 995Ω is connected across a cell of emf 3V and internal resistance 5Ω. Find the potential difference across the voltmeter, that across the terminals of the cell and percentage error in the reading of voltmeter.
View SolutionA voltmeter of resistance 994Ω is connected across a cell of emf 1 V and internal resistance 6Ω. Find the potential difference across the voltmeter, that across the terminals of the cell and percantage error in the reading of the voltmeter.
View Solution
Knowledge Check
A voltmeter has a resistance of 50Ω is connected across a cell of e.m.f. 2V and internal resistance 10Ω. The reading of voltmeter is
A1.667VB16.7VC167VD0.167VA cell of emf 2 V and internal resistance 0.1Ω is connected with a resistance of 3.9Ω The voltage across the cell terminal will be
A1.95VB1.90VC0.50VD2.00VA voltmeter of resistance 1000Ω is connected across a resistance of 500Ω in the given circuit. What will be the reading of voltmeter
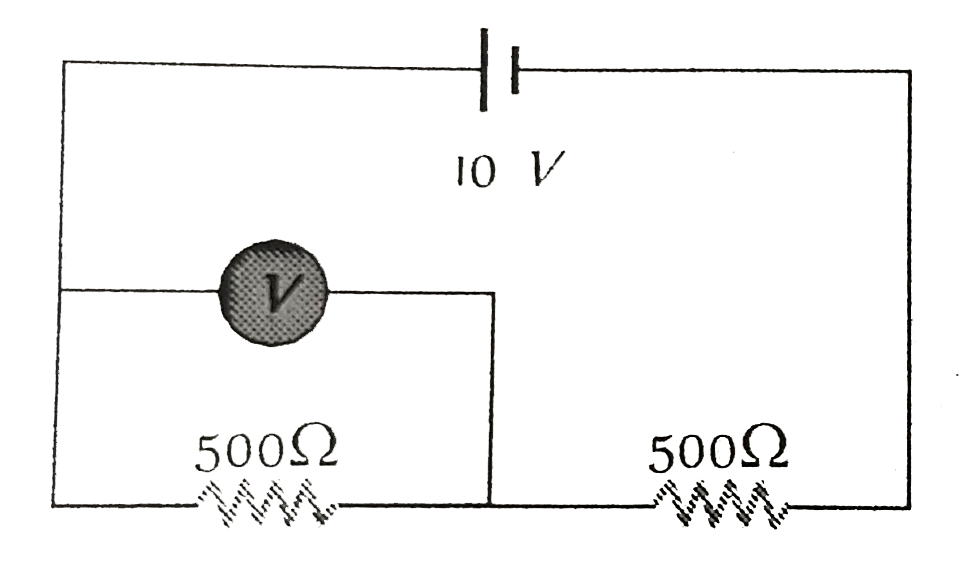 A1VB2VC6VD4V
A1VB2VC6VD4V
(a) Derive a relation between the internal resistance, emf and terminal potential difference of a cell from which current I is drawn. Draw V vs I graph for the cell and explain its significance.
(b) A voltmeter of resistance 988Ω is connected across a cell of emf 2 V and internal resistance 2Ω. Find the potential difference across the voltmeter and also across the terminals of the cell. Estimate the percentage error in the reading of the voltmeter.
View SolutionA voltmeter has resistance of 100 Ω . What will be its reading when it is connected across a cells of e.m.f 2 V and internal resistance 20 Ω ?
View SolutionA voltmeter has a resistance of 1000Ω. What will be its reading when it is connected across a cell of emf 2V and internal resistance 10Ω ?
View SolutionA voltmeter resistance 500Ω is used to measure the emf of a cell of internal resistance 4Ω. The percentage error in the reading of the voltmeter will be
View SolutionA cell of emf 2.0 V and internal resistance 0.1 Ω is connected with a resistance of 3.9Ω. The voltage across the cell terminals will be
View Solution
