A wave pulse is generated in a string that lies along x−axis. At the points A and B, as shown in figure, if RA and RB are ratio of magnitudes of wave speed to the particle speed, then
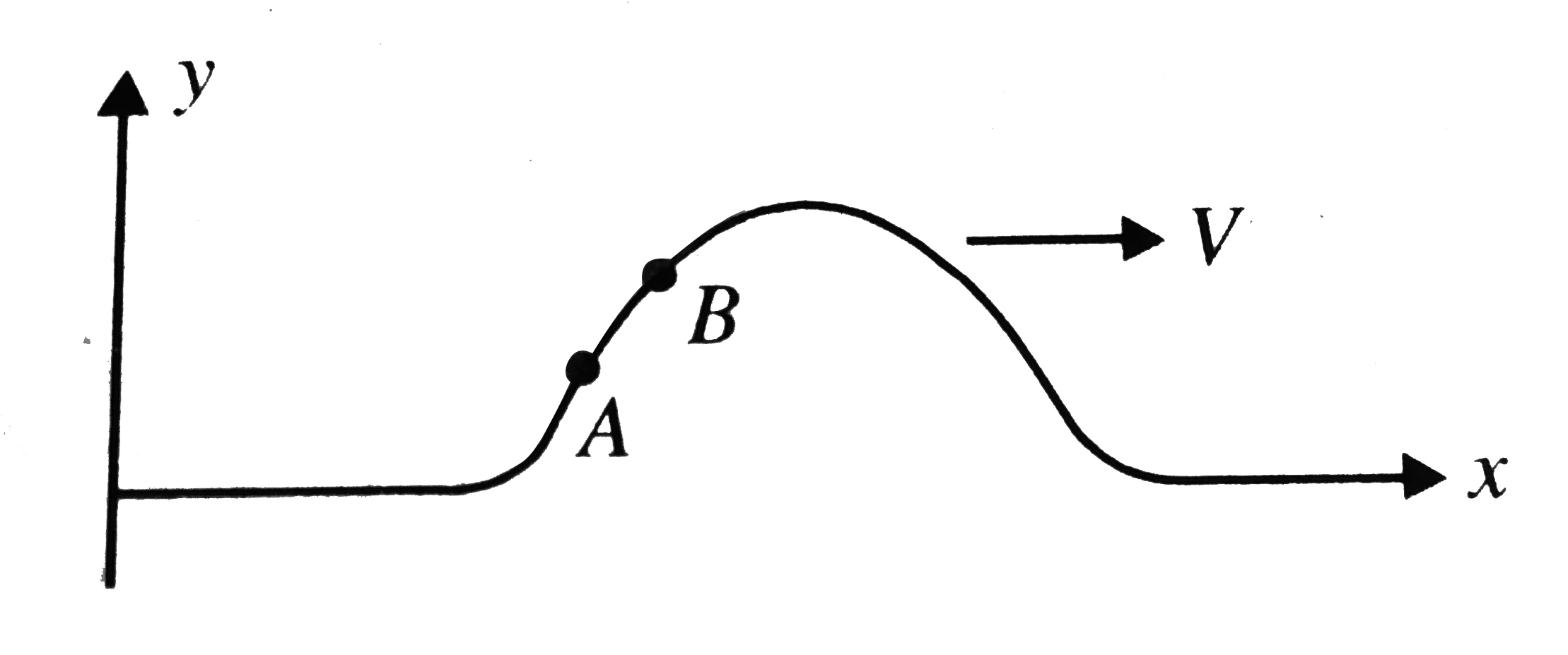
RA>RB
RB>RA
RA=RB
Information is not suficient to decide.
The correct Answer is:A
Slope at any point on the string in wave motion represents the ratio of particle speed to wave speed
implies slopeB>slopeA
hence RA>RB
Topper's Solved these Questions
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Advance MCQs with One or More Options Correct
30 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Unsolved Numerical Problems for Preparation of NSE, INPhO & IPhO
135 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Conceptual MCQs Single Option Correct
24 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
- X-RAYSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - X-RAYSEXERCISE - Unsolved Numerica Problem for Preparation
23 Videos
Similar Questions
A wave pulse is generated in a string that lies along x-axis. At the points A and B, as shown in figure, if
RAandRB
are ratio of wave speed to the particle speed respectively then :
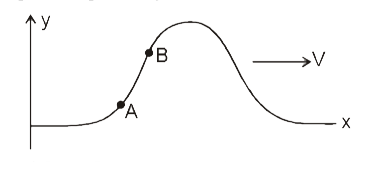
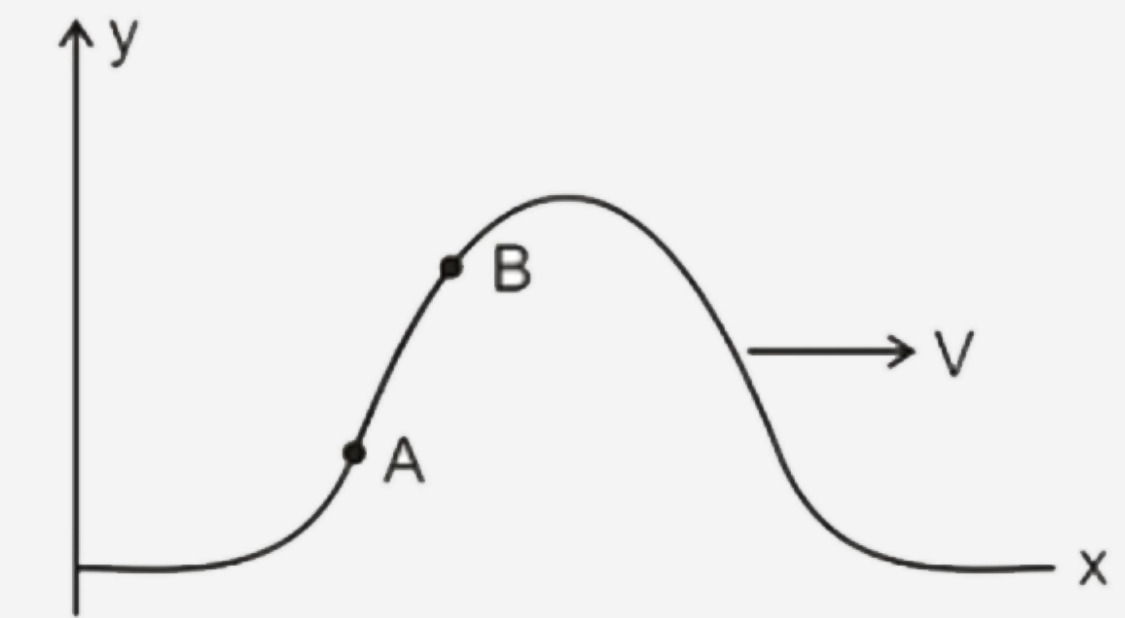
View SolutionA wave pulse is generated in a string that lies along x- axis. At the points A and B, as shown in the figure, if RAandRB are the ratio of wave speed to the particle speed respectively then:
View Solution
Knowledge Check
A particle moves from A to B in a circular path of radius R covering an angle θ as shown in figure. Find the ratio of magnitude of distance and magnitude of displacement of the particle.
 Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2
Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2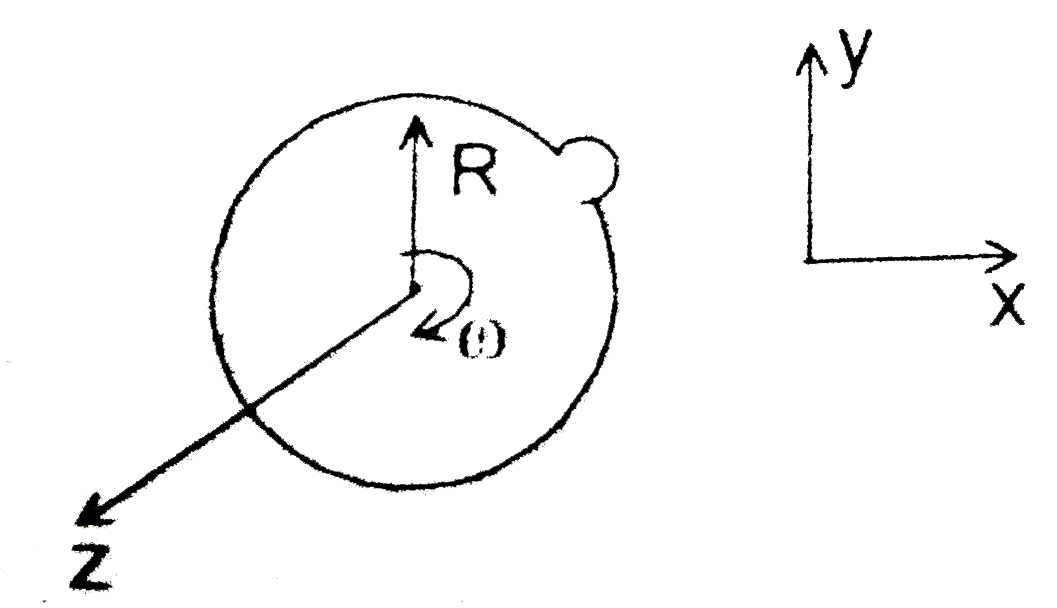
A small pulse is generated on a ring rotating with constant angular velocity ω as shown in the figure. Then the speed of pulse with respect to ground.AωRBωR/2C2ωRDzeroA particle moves along on a road with constant speed at all points as shown in figure. The normal reaction of the road on the particle is :
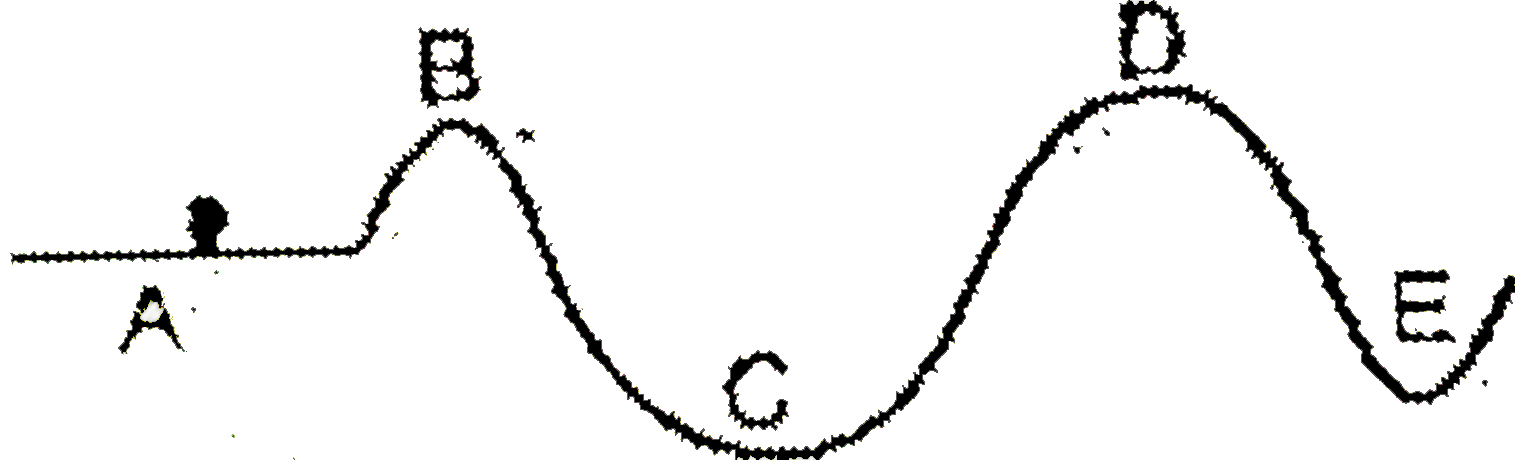 ASame at all pointsBMaximum at point BCMaximum at point CDMaximum at point E
ASame at all pointsBMaximum at point BCMaximum at point CDMaximum at point E
A point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionFind speed of the wave generated in the string as in the situation shown.
Assume that the cord is light
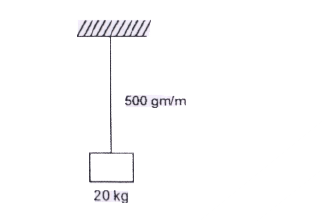
View Solution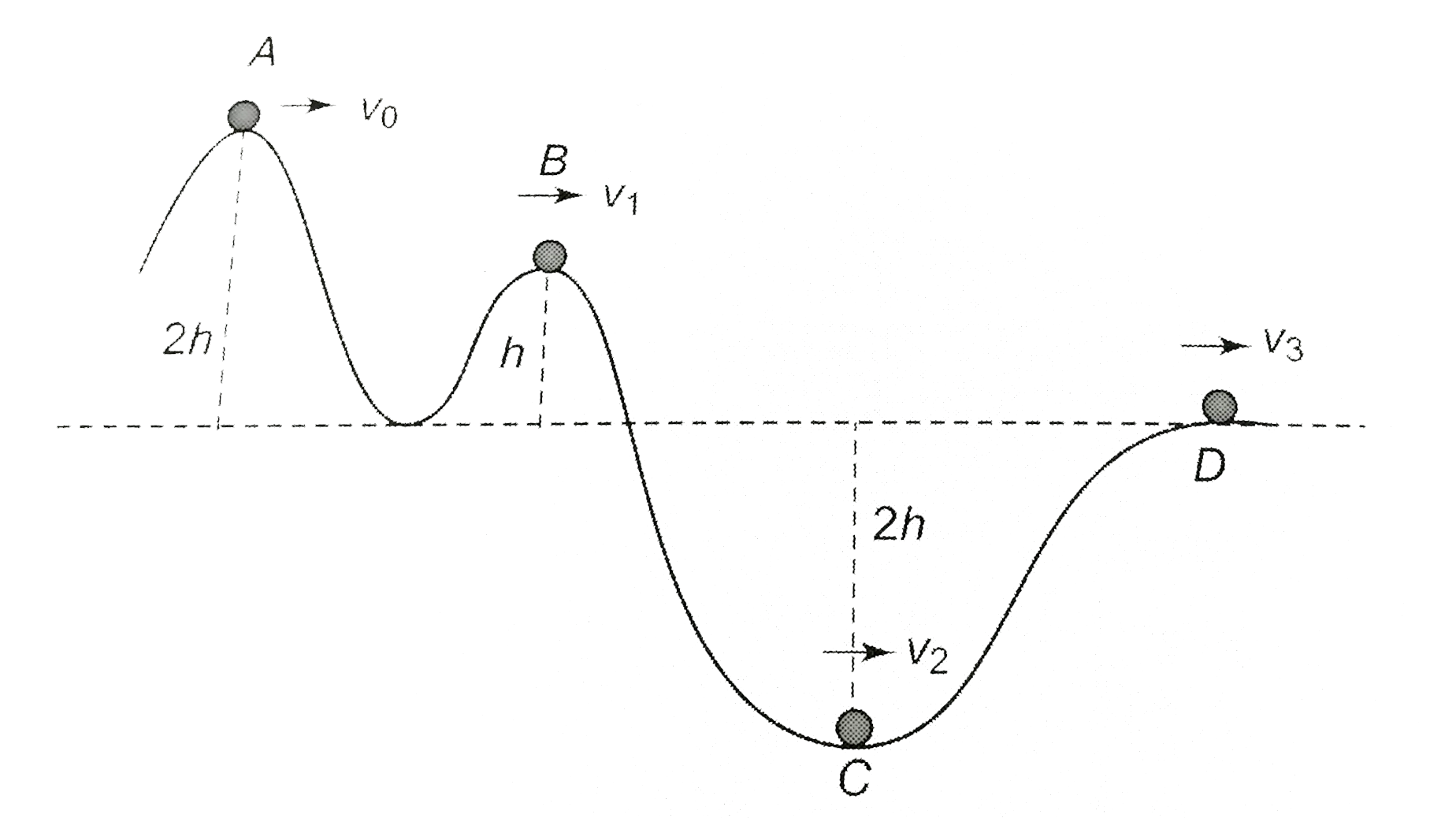
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and D
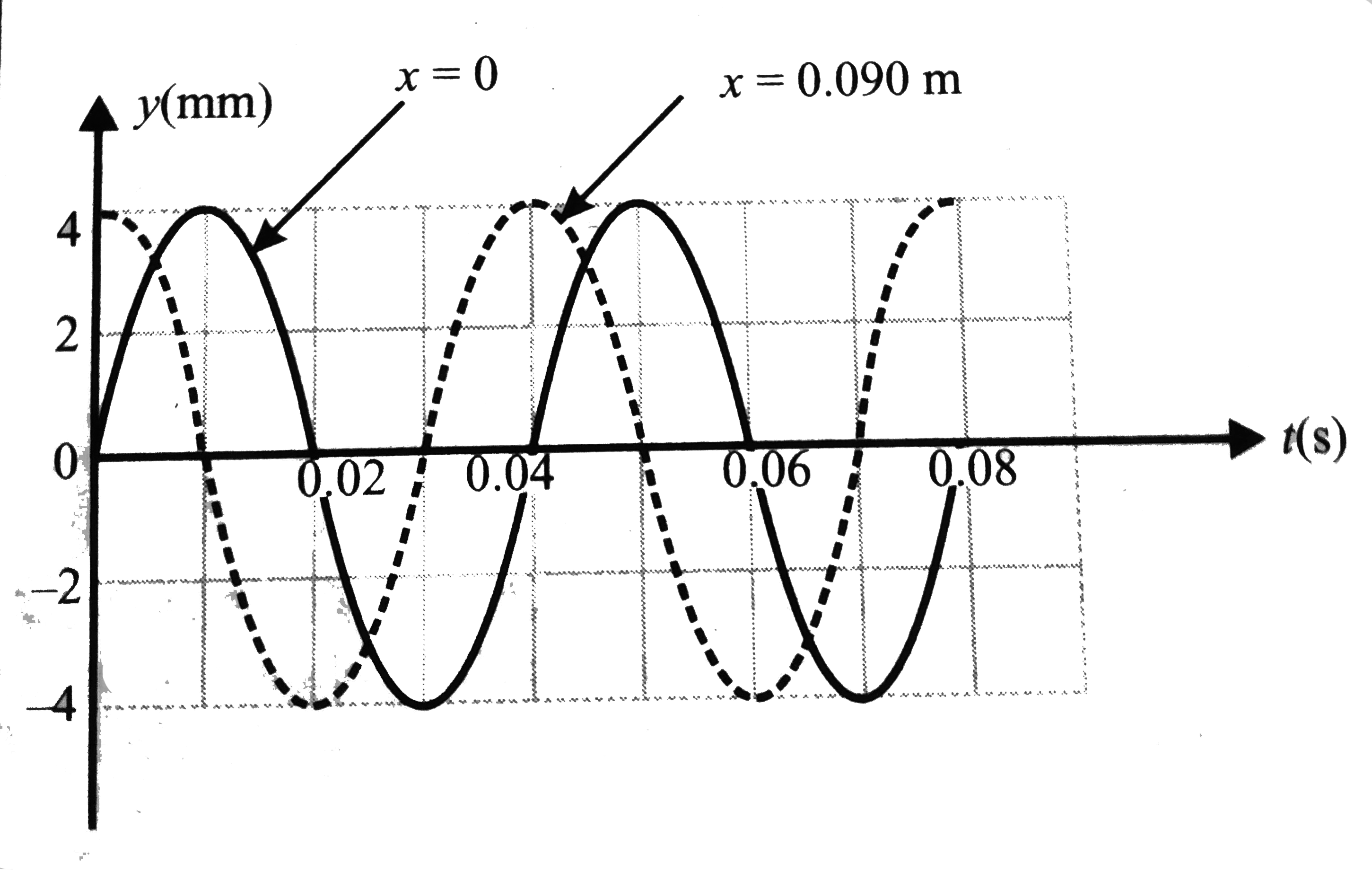
View SolutionA sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?
View SolutionA simple harmonic plane wave propagatees along x-axis in a medium. The displacement of the particle as a function of time is shown in figure, for x=0(curve 1) and x=7 (curve 2)
The two particle are with a span of onewavelength.
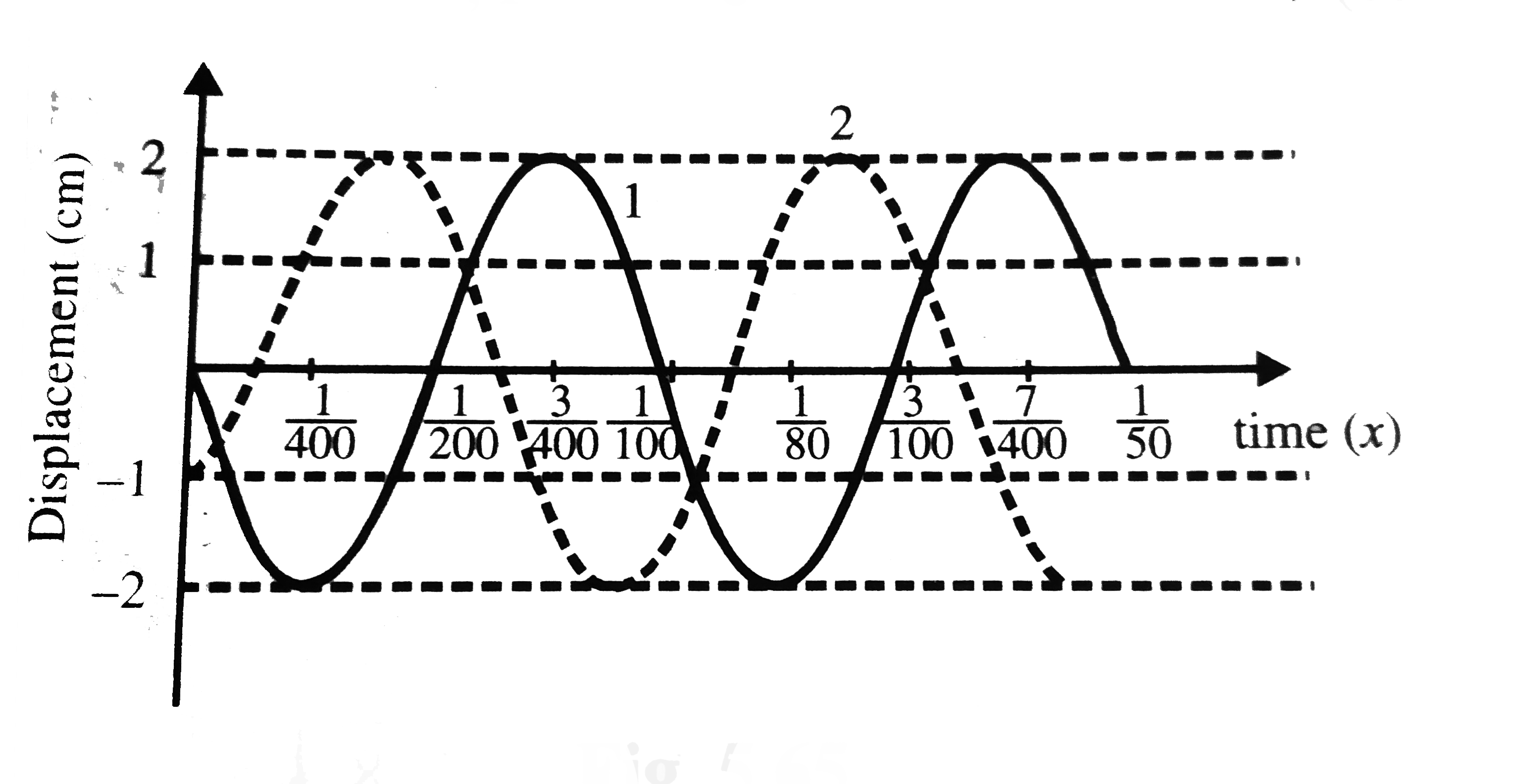
The speed of the wave is
View Solution
