A wave pulse is travelling on a string of linear mass density 1.0gcm−1 under a tension of 1 kg wt. Calculate the time taken by the pulse to travel a distance of 50 cm on the string.Given g=10ms−2.
The correct Answer is:0.05 s
To solve the problem of calculating the time taken by a wave pulse to travel a distance of 50 cm on a string, we will follow these steps:
Step 1: Convert the linear mass density to standard units
The given linear mass density is 1.0g/cm(−1). We need to convert this to kg/m.
1.0g/cm(−1)=1.0×10−3kg/m=0.01kg/m
Step 2: Calculate the tension in standard units
The tension is given as 1kg wt. We need to convert this to Newtons (N). Since 1kg wt=gN and g=10m/s2:
T=1kg×10m/s2=10N
Step 3: Calculate the speed of the wave on the string
The speed of a wave on a string is given by the formula:
v=√Tμ
Where:
- T is the tension (in N)
- μ is the linear mass density (in kg/m)
Substituting the values we have:
v=√10N0.01kg/m=√1000=31.62m/s
Step 4: Calculate the time taken to travel 50 cm
We need to find the time t taken to travel a distance d=50cm=0.5m. The formula for time is:
t=dv
Substituting the values:
t=0.5m31.62m/s≈0.0158s
Step 5: Final answer
The time taken by the pulse to travel a distance of 50 cm on the string is approximately:
t≈0.0158s≈0.016s
The given linear mass density is 1.0g/cm(−1). We need to convert this to kg/m.
The tension is given as 1kg wt. We need to convert this to Newtons (N). Since 1kg wt=gN and g=10m/s2:
The speed of a wave on a string is given by the formula:
- T is the tension (in N)
- μ is the linear mass density (in kg/m)
We need to find the time t taken to travel a distance d=50cm=0.5m. The formula for time is:
The time taken by the pulse to travel a distance of 50 cm on the string is approximately:
Topper's Solved these Questions
Similar Questions
A wave pulse is travelling on a string of linear mass density 10gcm−1 under a tension of 1kg wt. Calculate the time taken by the pulse to travel a distance of 50cm on the string. Take g=10m/s2.
View SolutionA way pulse is travelling on a string of linear mass density 6.4×10−3kgm−1 under a load of 80kgf. Calculate the time taken by the pulse to traverse the string, if its length is 0.7m.
View Solution
Knowledge Check
Figure shows a string of linear mass density 1.0gcm−1 on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of 50cm on the string. Take g=10ms−2
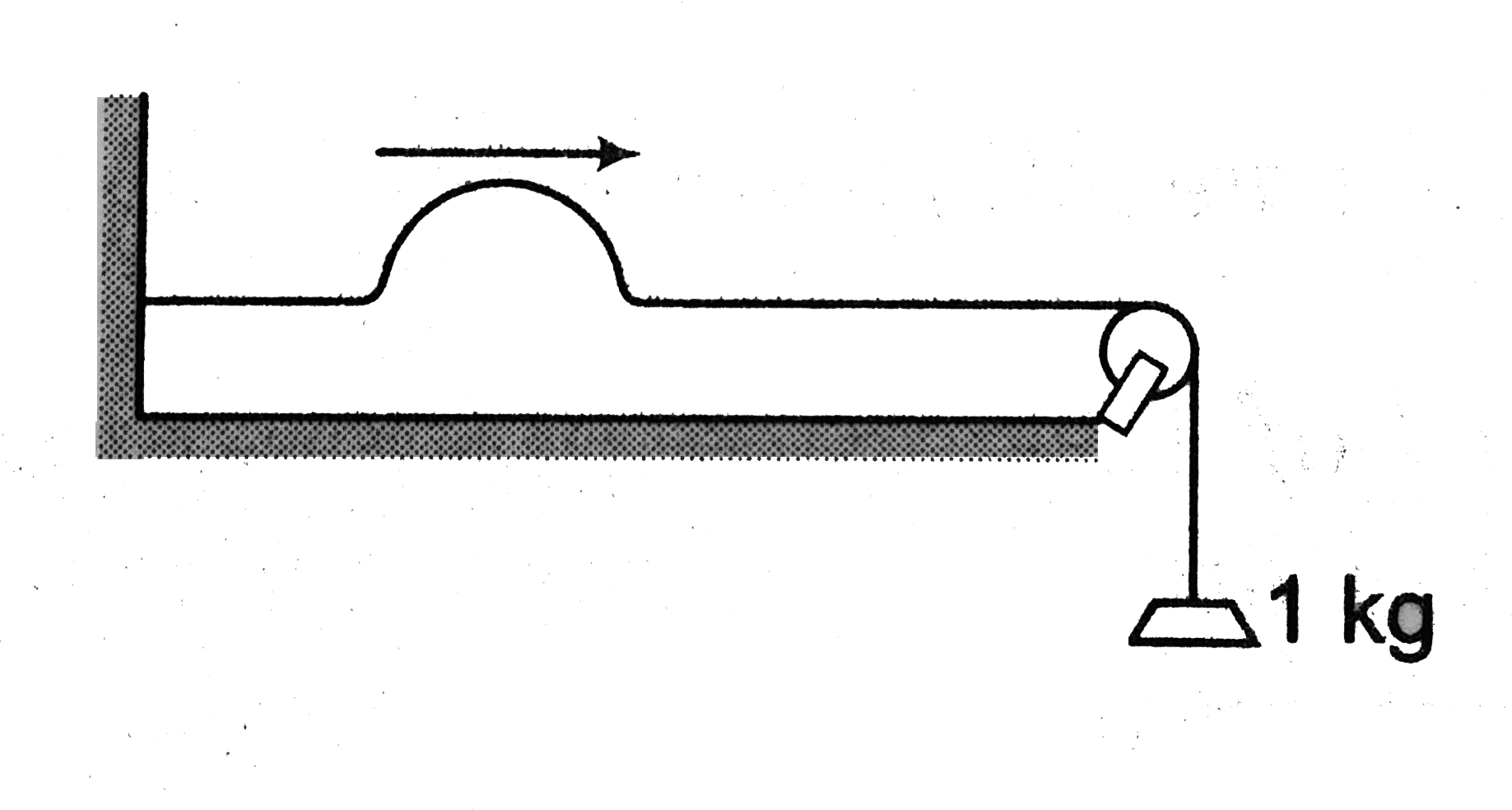 A0.5 sB0.0005 sC0.05 sD5 s
A0.5 sB0.0005 sC0.05 sD5 sA 100 Hz sinusoidal wave is travelling in the positive x - direction along a string with a linear mass density of 3.5×10−3kgm−1 and a tension of 35 N. At time t =0 ,the point x=0 has zero displacement and the slope of the string is π/20 then select the wrong alternative.
Avelcoity of wave is 100 m/sBangular velocity is (200π) rad /sCAmplitude of wave is 0.025 mDnone of the above
Figure showa a string of linear mass density 1.0gcm−1onwhichawaveps–eistravell∈g.F∈dthetimetakenbytheps–e∈travell∈gthroughadistanceof50cmonthestr∈g.Takeg=10 ms^-2.
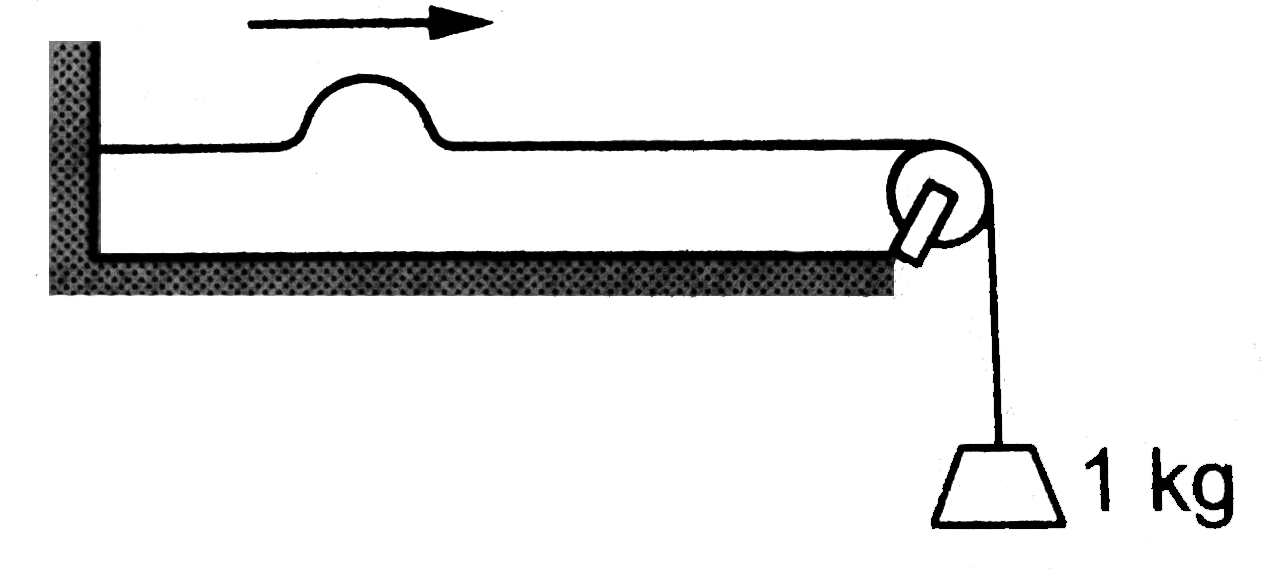
View SolutionFigure shows a string of linear mass density 1.0g/cm on which a wave pulse is travelling. Find the time taken (in milli second) by the pulse in travelling through a distance of 60cm on the string. Take g=10m/s2.

View SolutionA 200Hz wave with amplitude 1mm travels on a long string of linear mass density 6g/m keep under a tension of 60N.
(a) Find the average power transmitted across a given point on the string.
(b) Find the total energy associated with the wave in a 2.0m long portion of the string.
View SolutionThe speed of a wave in a streched string is 20ms−1 and its frequency is 50 Hz. Calculate the phase difference in radian between two points situated at a distance of 10 cm on the string.
View SolutionThe fundamental frequency in a string increases in the ratio 1 : 4 on increasing the tension by 10 kg wt. Calculate the initial tension of the string.
View SolutionA string 50 cm long is under a tension of 20N force. Caculate the frequency of fundamental mode given that mass of the string is 1 g.
View Solution
