A wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 att=0. Where will this maximum be located at t=5s?
v=40cm/s
As velocity of a wave is constant, location of maximum after 5 s is given by 40×5=200cm along the negative x-axis at x=−2m
Topper's Solved these Questions
Similar Questions
The equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View SolutionThe equation of a wve travelling on a string stretched along the X-axis is given by
y=Ad−(xatT)2
a. Write the dimensions of A, a and T. b. Find the wave speed. c.In which direction is the wave travelling? d.Where is the maximum of the pulse located at t=T?Att=2T?
View Solution
Knowledge Check
A wave pulse on a string has the dimension at time t=0 as shown below is reflected from a fixed end O.
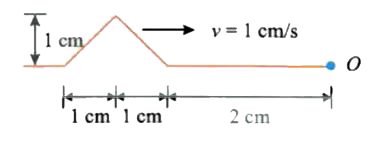
Its dimensions at t=3s isA B
B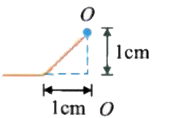 C
C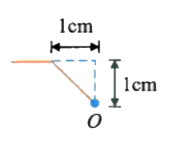 D
D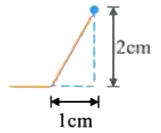
A wave pulse on a string on a string has the dimension shown in figure. The wave speed is v=1 cm /s . If point O is a free end. The shape of wave at time t = 3s si
 A
A B
B C
C D
D
A wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at t = 0 is given by g(x)=Asin(xa), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time 1, if the wave speed is v.
View SolutionA wave pulse is travelling on a string at 2m/s along positive x-directrion. Displacement y of the particle at x = 0 at any time t is given by
y=2t2+1 Find
Shape of the pulse at t = 0 and t = 1s.
View SolutionFigure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=s, 2s and 3s.

View SolutionA simple harmonic oscillator at the point x=0 genrates a wave on a rope. The oscillator operates at a frequency of 40.0 Hz and with an amplitude of 3.00 cm. the rope has a linear mass density of 50.0g/m and is strectches with a tension of 5.00 N. (a) determine the speed of the wave. (b) find the wavelength. (c ) write the wave function y(x,t) for the wave, Assume that the oscillator has its maximum upward displacement at time t=0. (d) find the maximum transverse acceleration at time t=0. (d) find the maximum transverse of points on the rope. (e) in the discussion of transverse waves in this chapter, the force of gravity was ignored. is that a reasonable assumption for this wave? explain.
View SolutionA transverse sinusoidal wave is moving along a string in the opposite direction of an x axis with a speed of 70m/s. At t=0 the string particle at x=0 has a transverse displacement of 4.0 cm and is not moving. The maximum transverse speed of the string particle at x=0 is 16m/s. (a) What is the frequency of the wave? (b) What is the wavelength of the wave? If y(x,t) =ymsin(kx±ωt+ϕ) is the form of the wave equation, what are (c) ym,(d)k,(e)ω(f)ϕ, and (g) the correct of sign in front of ω?
View SolutionA wave propagates on a string in the positive x-direction at a velocity u. The shape of the string at t=t0 is given by g(x,t0)=Asin(xa) . Write the wave equation for a general time t.
View Solution
