A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
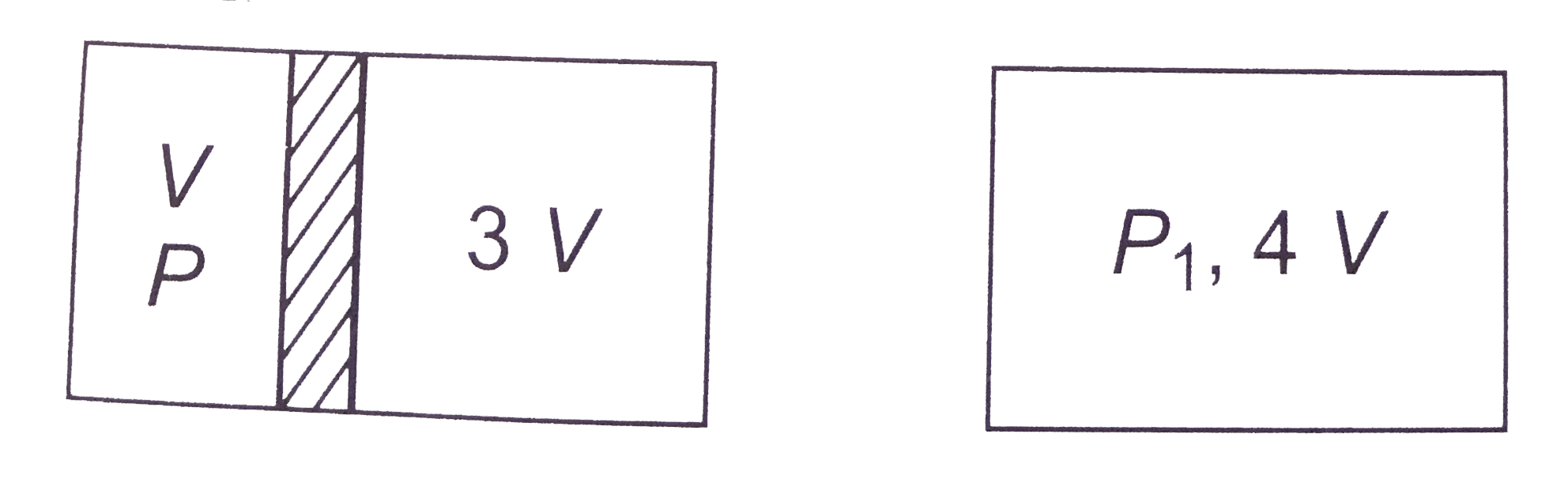
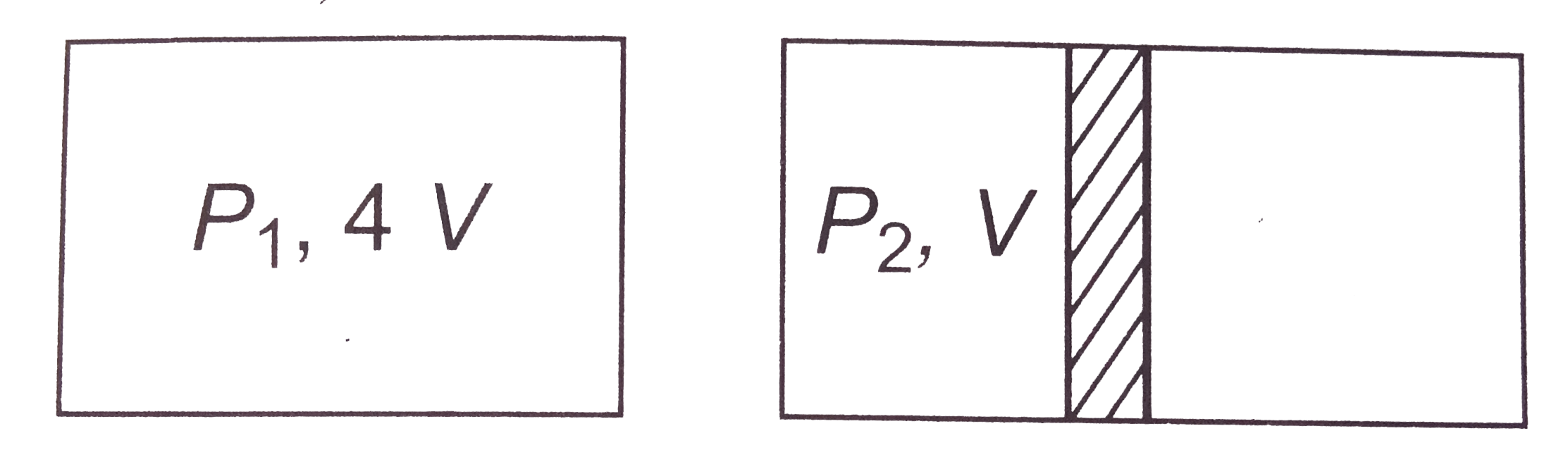
In free expansion, no work is done, temperature remains same. Since number of moles remains same
n=PVRT=P1.4VRT
P1=P4
In the case compression is adiabatic
P1(4V)γ=P2Vγ⇒P2=4γP1=(4)(3/2)(P4)=2P
ΔU=−ΔWadi=P2V2−P1V1γ−1=2P.V−P4.4V32−1
=2PV
=2×2×105×1×10−3=400J
ΔU=nCVΔT=nRΔTγ−1=2×8.3ΔT32−1=33.2ΔT
ΔT=ΔU33.2=40033.2=12K
Final temperature=T1+ΔT+(27+273)+12=312K
(Room temperature 27∘C)
Topper's Solved these Questions
Similar Questions
A mass less piston divides a thermally insulated cylinder into two parts having volumes V = 2.5 litre and 3 V = 7.5 litre. 0.1 mole of an ideal gas is confined into the part with volume V at a pressure of P=105N/m2. The other part of the cylinder is empty. The piston is now released and the gas expands to occupy the entire volume of the cylinder. Now the piston is pressed back to its initial position. Find final temperature of the gas.
[Take R=253Jmol−1K−1 and γ=1.5 for the gas]
View SolutionA weightless piston divides a thermally insulated cylinder into two equal parts. One part contains one mole of an ideal gas with adiabatic exponent γ, the other is evacuated. The initial gas temperature is T0. The piston is released and the gas fills the whole volume of the cylinder. Then the piston is slowly displaced back to the initial position. Find the increment of the internal energy and entropy of the gas was resulting from these two processes.
View Solution
Knowledge Check
A vertical thermally insulated cylinder of volume V contain n moles of an ideal monoatomic gas under a weightless piston. A load of weight W is placed on the piston as a result of which the piston is displaced. If the initial temp of the gas is 300K, area of piston is A and atmospheric pressure P0. (take W=P0A). Determine the value of final temperature of the gas
A375KB425KC475KD515KA gas is contained in a metallic cylinder fitted with a piston.The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
AincreasesBDecreasesCRemans constantDIncreases or decreases depending on the nature of the gas.
A masslesss piston divides a closed thermallyy insulated cylinder into two equal parts. One part contains M = 28 g of nitrogen. At this temperature, one-third of molecules are dissociated into atoms and the other part is evacuated. The piston is released and the gas fills the whole volume of the cylinder at temperature T0. Then, the piston is slowly displaced back to its initial position. calculate the increases in internal energy of the gas. Neglect further dissociation of molecules during, the motion of the piston.
View SolutionA gas filled in a cylinder fitted with movable piston is allowed to expand. What is the nature of the work done by the gas?
View SolutionA piston divides a closed gas cylinder into two parts. Initially the piston is kept pressed such that one part has a pressure P and volume 5V and the other part has pressure 8P and volume V, the piston is now left free. Find the new pressure and volume for the isothermal and aidabatic process. (γ=1.5)
View Solution(i) A conducting piston divides a closed thermally insulated cylinder into two equal parts. The piston can slide inside the cylinder without friction. The two parts of the cylinder contain equal number of moles of an ideal gas at temperature T0. An external agent slowly moves the piston so as to increase the volume of one part and decrease that of the other. Write the gas temperature as a function of ratio (β) of the volumes of the larger and the smaller parts. The adiabatic exponent of the gas is γ.
(ii) In a closed container of volume V there is a mixture of oxygen and helium gases. The total mass of gas in the container is m gram. When Q amount of heat is added to the gas mixture its temperature rises by ΔT. Calculate change in pressure of the gas.
View SolutionA gas is filled in a cylinder fitted with a piston at a definite temperature and pressure. Explain on the basis of kinetic theory why on pulling the piston out, the pressure of decreases.
View SolutionA gas is filled in a cylinder fitted with a piston at a definite temperature and pressure. Explain on the basis of kinetic theory why on pulling the piston out, the pressure of decreases.
View Solution
