A weightless rod of length l with a small load of mass m at the end is hinged at point A as shown and occupies a strictly vertical position, touching a body of mass M. A light jerk sets the system in motion.
a. For what mass ratio M/m will the rod form an angle α=π/6 with the horizontal at the moment of the separation from the body?
b. What will he the velocity u of the body at this moment? Friction should be neglected.
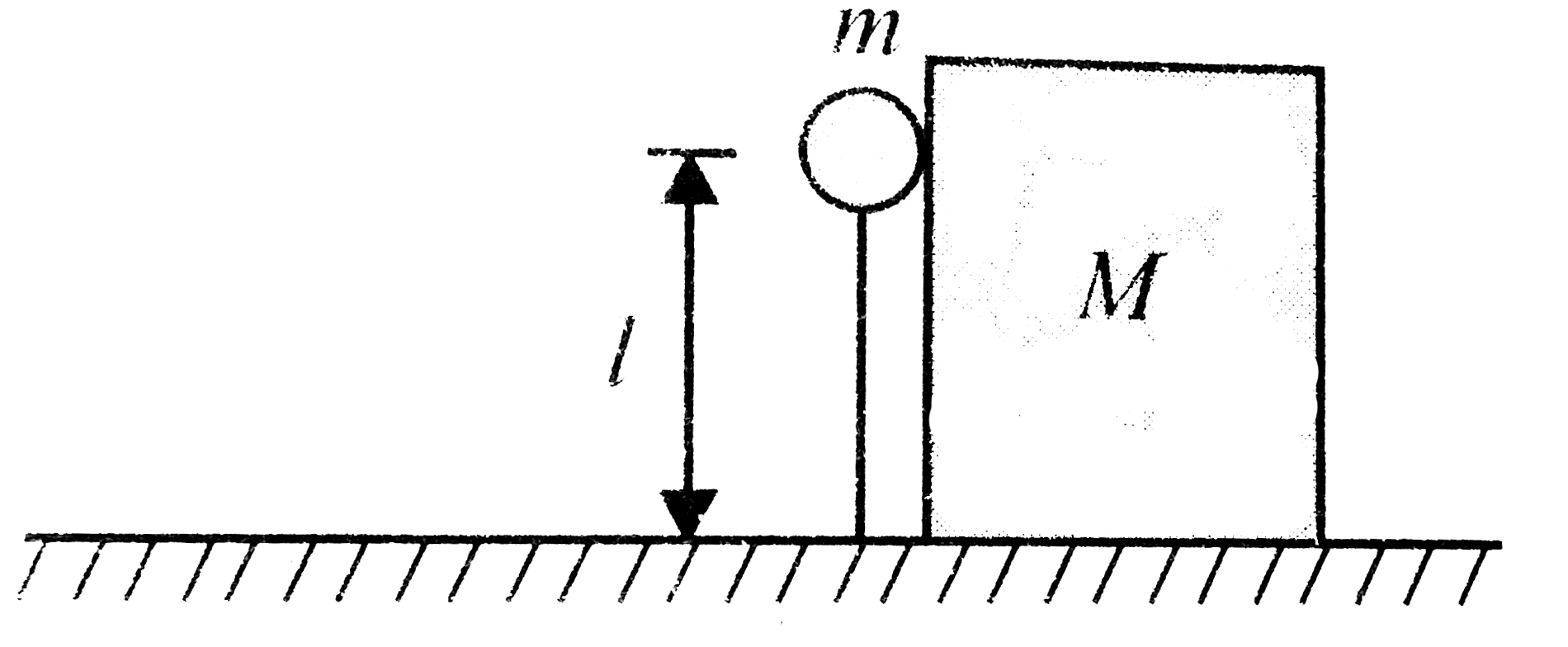
The correct Answer is:√gl2
a=atsinα−accosα
At the time of separation
For M,ΣFx=0 and a=0

Acceleratin of the load in horizontal direction
a=0=a1sinα−v2lcosα
atsinα=v2lcosα
But at=gcosα
Hence v=√glsinα
u=vsinα=sinα√glsinα
mgl=mglsinα+mv22+12Mv2sinα
Mm=2−3sinαsin3α=4
u=vsinα=12√gl2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct97videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.411videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A weightless rod of length l with a small load of mass m at the end is hinged at point A (Fig.) and occupies a strictly vertical position, touching a body of mass M. A light jerk sets the system in motion . For what mass ratio M/m will the rod form an angle α=π/6 with the horizontal at the moment of the separation from the body ? What will be the velocity u of the body at this moment ? Friction should be neglected.
 View Solution
View SolutionA weightless rod of length l with a small load of mass m at one of its end is held vertical with its lower end hinged on a horizontal surface. The load touches a wedge of mass M in this position. A slight jerk towards right sets the system in motion (see figure), with rod rotating freely in vertical plane about its lower end. There is no friction.
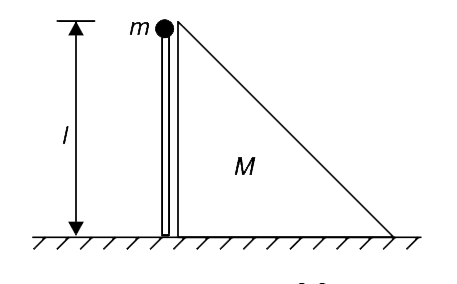
(a) For what mass ratio Mm will the rod form an angleθ=π/3 with the vertical at the moment the load separates from the wedge? (b) What is speed of the wedge at that moment? Neglect friction.View Solution
Knowledge Check
- Question 1 - Select One
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lg - Question 2 - Select One
A rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14 - Question 3 - Select One
A uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 A2√5g7lB2√6g7lC√3g7lD2√gl
A2√5g7lB2√6g7lC√3g7lD2√gl
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 View Solution
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View Solution

