A wheel is at rest. Its angular velocity increases uniformly and becomes 60 rad/sec after 5 sec. The total angular displacement is
600 rad
75 rad
300 rad
150 rad
The correct Answer is:D
To solve the problem, we need to find the total angular displacement of the wheel as it accelerates uniformly from rest to an angular velocity of 60 rad/sec over a time period of 5 seconds. We can use the equations of motion for rotational motion to find the angular displacement.
1. Identify Given Values:
- Initial angular velocity (ω0) = 0 rad/sec (the wheel is at rest)
- Final angular velocity (ωf) = 60 rad/sec
- Time (t) = 5 sec
2. Calculate Angular Acceleration (α):
- Use the formula for angular acceleration:
α=ωf−ω0t
- Substitute the known values:
α=60rad/sec−0rad/sec5sec=605=12rad/sec2
3. Use the Angular Displacement Formula:
- The formula for angular displacement (θ) when starting from rest is:
θ=ω0t+12αt2
- Since ω0=0, the equation simplifies to:
θ=12αt2
4. Substitute Values into the Displacement Formula:
- Substitute α=12rad/sec2 and t=5sec:
θ=12×12rad/sec2×(5sec)2
- Calculate (5sec)2=25sec2:
θ=12×12×25
- Now calculate:
θ=6×25=150radians
5. Final Answer:
- The total angular displacement of the wheel is θ=150radians.
- Initial angular velocity (ω0) = 0 rad/sec (the wheel is at rest)
- Final angular velocity (ωf) = 60 rad/sec
- Time (t) = 5 sec
- Use the formula for angular acceleration:
α=ωf−ω0t
- Substitute the known values:
α=60rad/sec−0rad/sec5sec=605=12rad/sec2
- The formula for angular displacement (θ) when starting from rest is:
θ=ω0t+12αt2
- Since ω0=0, the equation simplifies to:
θ=12αt2
- Substitute α=12rad/sec2 and t=5sec:
θ=12×12rad/sec2×(5sec)2
- Calculate (5sec)2=25sec2:
θ=12×12×25
- Now calculate:
θ=6×25=150radians
- The total angular displacement of the wheel is θ=150radians.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on centre of mass)
12 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular displacement, velocity and acceleration)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
A wheel starts from rest and attains an angular velocity of 20 radian/s after being uniformly accelerated for 10 s. The total angle in radian through which it has turned in 10 second is
View SolutionThe figure shows a graph of the angular velocity of a rotating wheel as a function of time. Although not shown in the graph, the angular velocity continues to increase at the same rate until t = 8.0 s. What is the angular displacement of the wheel from 0 to 8.0 s?
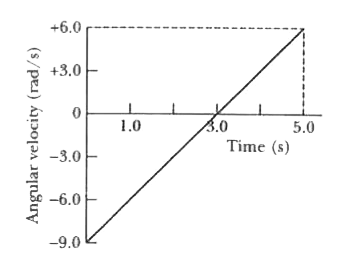
View Solution
Knowledge Check
A wheel is a rest. Its angular velocity increases uniformly and becomes 80rads−1 after 5 s. The total angular displacement is
A800 radB400 radC200 radD100 radA wheel is at rest. Its angular velocity increases uniformly and becomes 80 radian per second after 5 second. The total angular displacement is :-
A800radB400radC200radD100radA wheel is at rest. Its angular velocity increases uniformly and becomes 80 radian per second after 5 second. The total angular displacement is :-
A800 radB400 radC200 radD100 rad
Starting from rest the fly wheel of a motor attains an angular velocity of 60rad/sec in 5 seconds. The angular acceleration obtained is
View SolutionA wheel starts from rest and acquires an angular velocity of 60rad/s in half a minute . Then its angular acceleration is
View SolutionA wheel starts rotating at 10 rad/sec and attains the angular velocity of 100 rad/sec in 15 seconds. What is the angular acceleration in rad/sec2?
View SolutionThe planes of two rigid discs are perpendicular to each other. They are rotating about their axes. If their angular velocities are 3 rad/sec and 4 rad/sec respectively, then the resultant angular velocity of the system would be
View SolutionA wheel starting with angular velocity of 10 radian/sec acquires angular velocity of 100 radian/sec in 15 seconds. If moment of inertia is 10kg−m2 , then applied torque (in newton-metre) is
View Solution
