A wheel of radius r and mass m stands in front of a step of height h. The least horizontal force which should be applied to the axle of the wheel to allow it to raise onto the step is
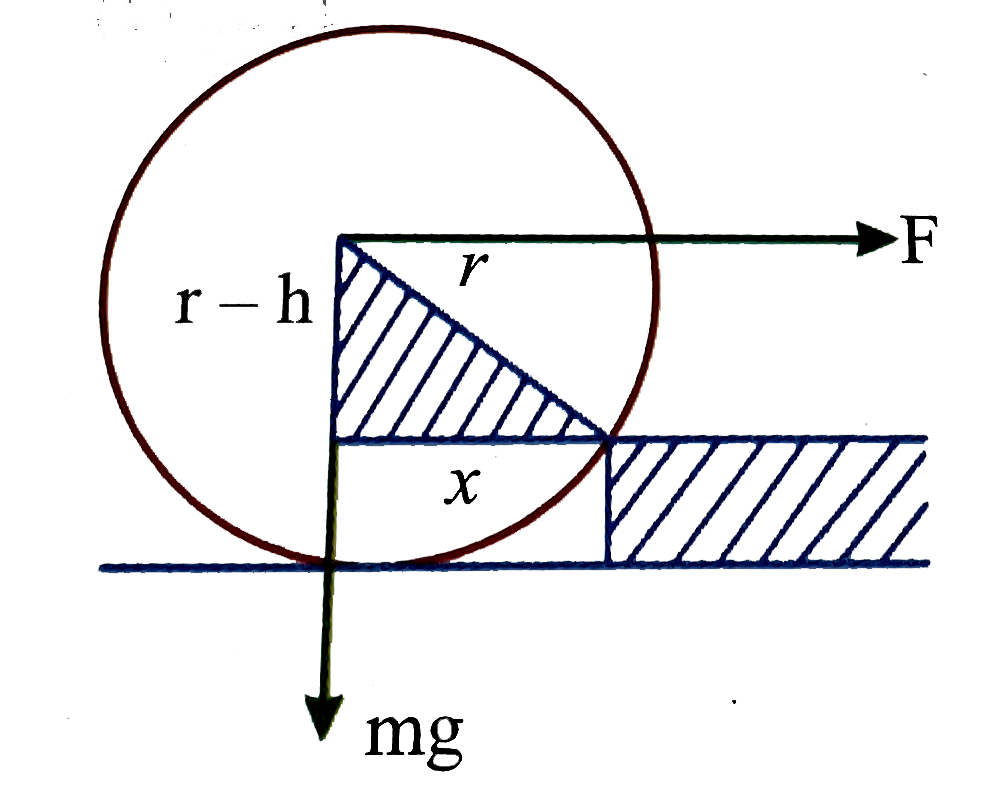
mgh(2r−h)r−h
mgh(r−h)
mg(√h(2r−h))r−h
mghr
The correct Answer is:C
Applying the condition of rotational equilibrium
F(r−h)=mgx
but r2=x2+(r−h)2⇒x=√h(2r−h)
∴F=mg√h(2r−h)r−h
Topper's Solved these Questions
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Level-v(Single answer)
23 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Multiple answer
6 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Intergers type question
11 Videos
- MAGNETISMBOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
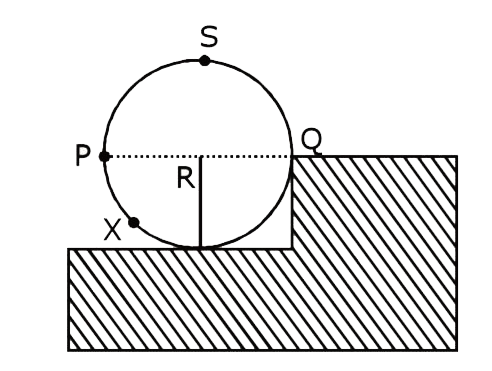
A wheel of radius R and mass M is placed at the bottom of a fixed step of height R as shown in the figure. A constant force is continuously applied on the surface of the wheel so that it just climbs the step without slipping. Consider the torque τ about an axis normal to the plane of the paper passing through the point Q. Which of the following options is/are correct?
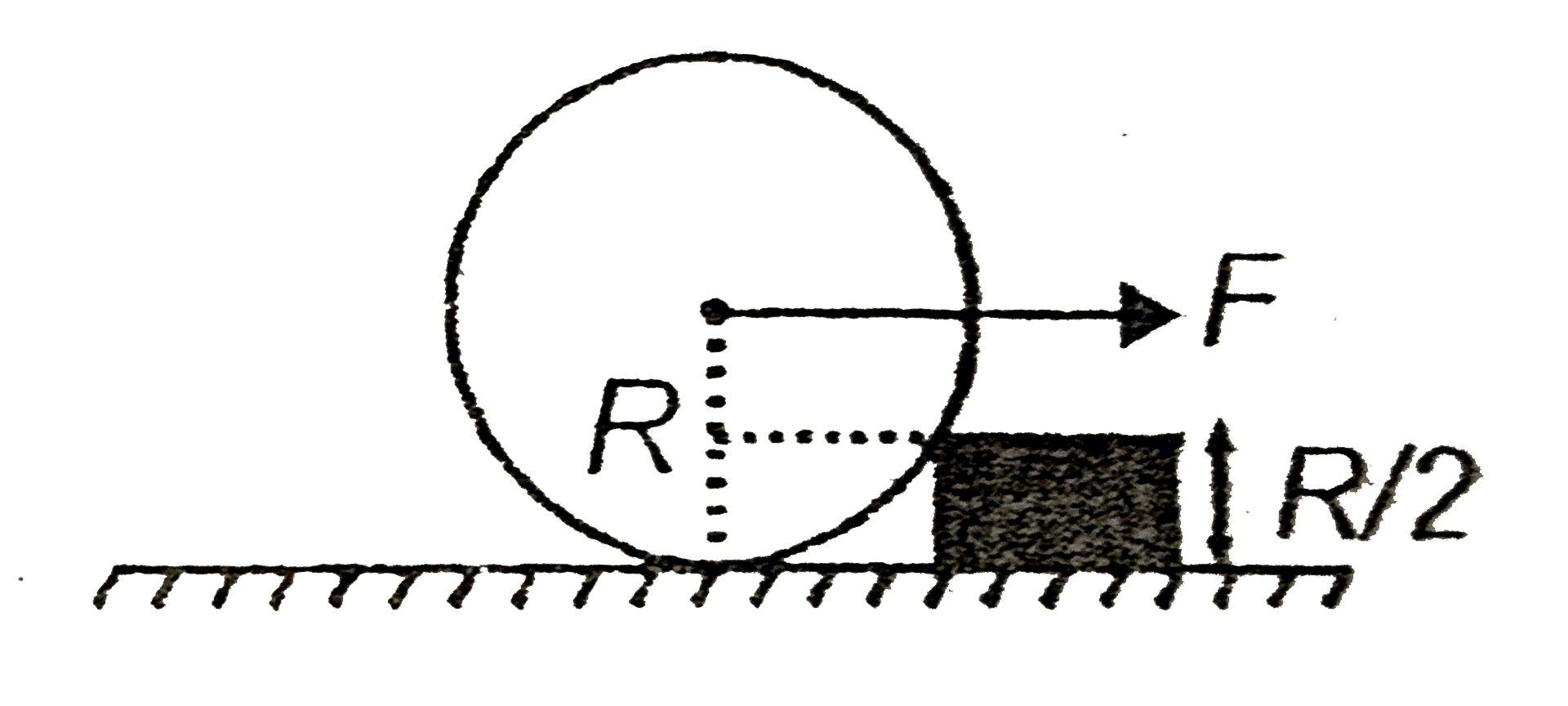
View SolutionThe minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2
View Solution
Knowledge Check
A heavy wheel of radius 20cm and weight 10kg is to be dragged over a step of height 10cm, by a horizontal force F applied at the centre of the wheel. The minimum value of F is
A20kgwtB1kgwtC10√3kgwtD10√2kgwtA roller of mass 300kg and of radius 50cm lying on horizontal floor is resting against a step of height 20cm. The minimum horizontal force to be applied on the roller passing through its centre to turn the roller on to the step is
A980NB1960NC2940ND3920NA vertical disc of mass 5kg and radius 50cm rests against a steo of height 25cm as shown in figure. What minimum horizontal force applied perpendicular to the axle will make the disc to climb the step ? Take g=10m/s2.
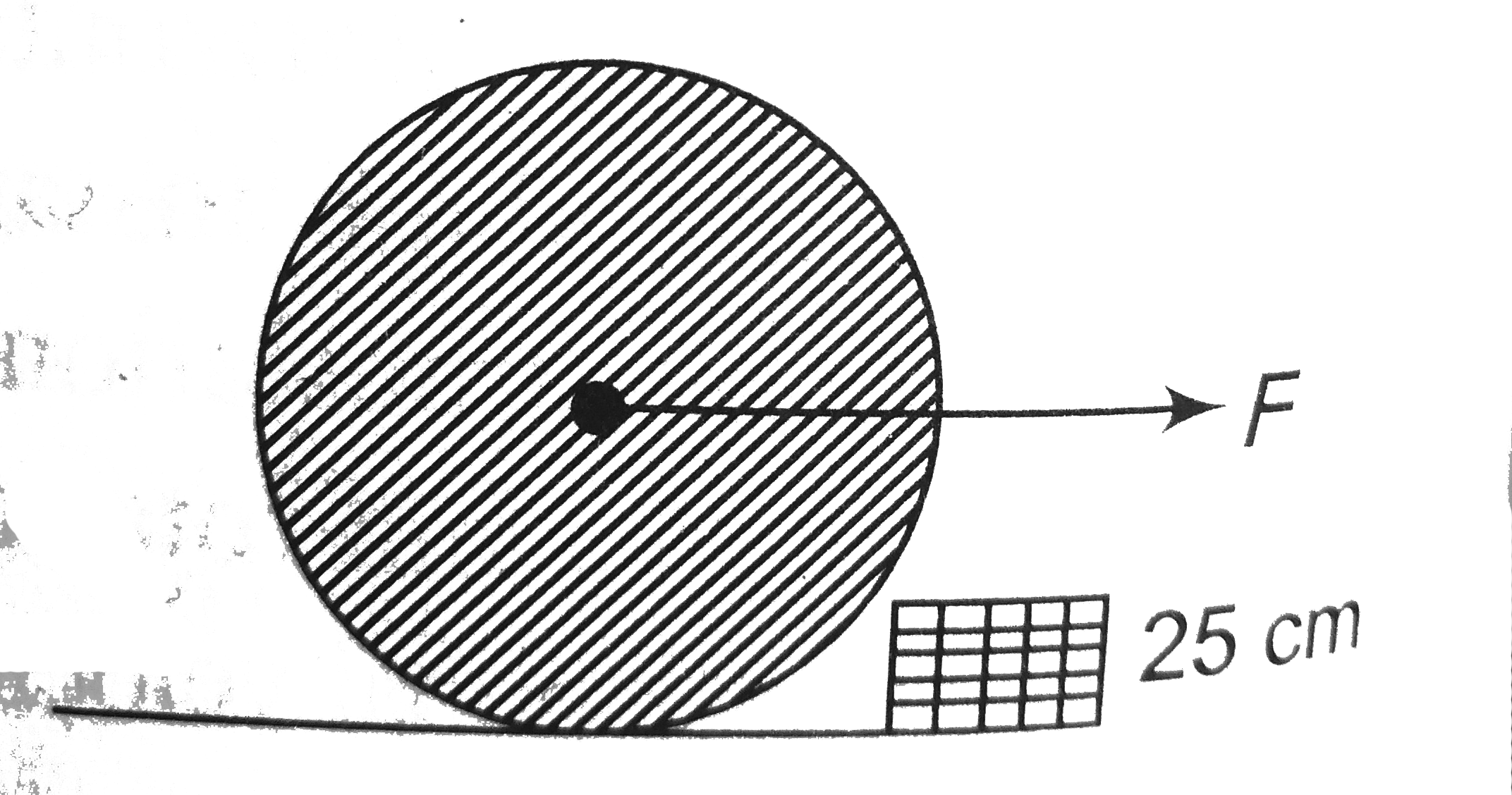 .A50 NB50√3NC25NDnone of these
.A50 NB50√3NC25NDnone of these
A wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
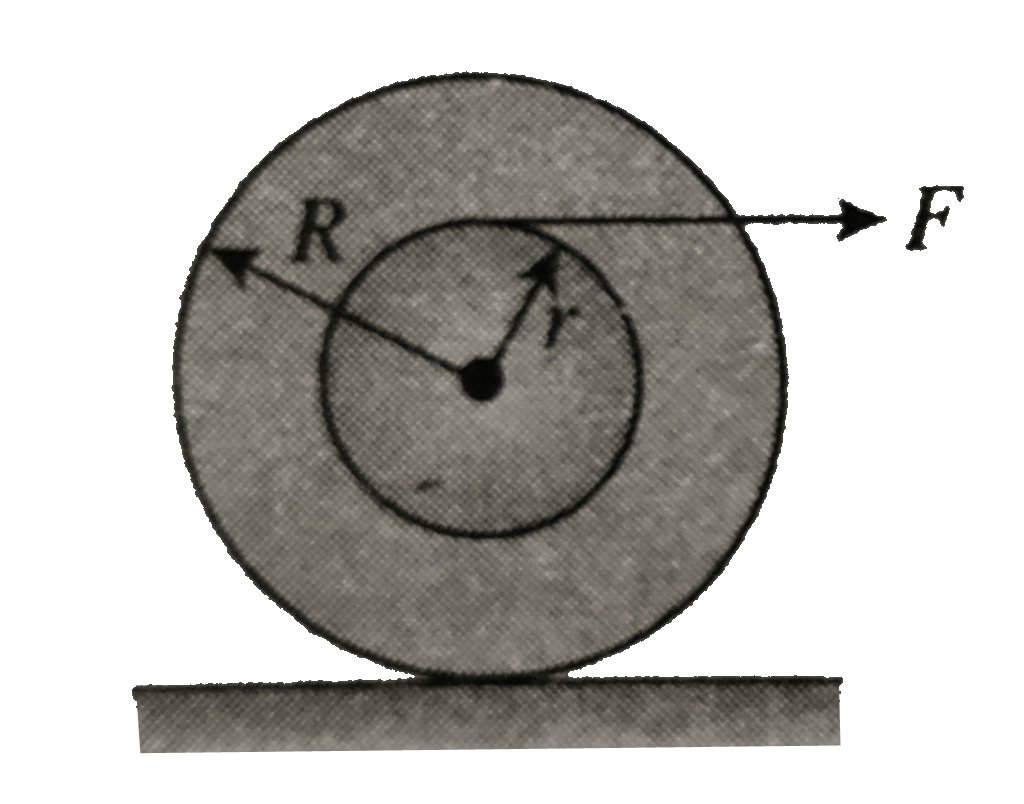
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
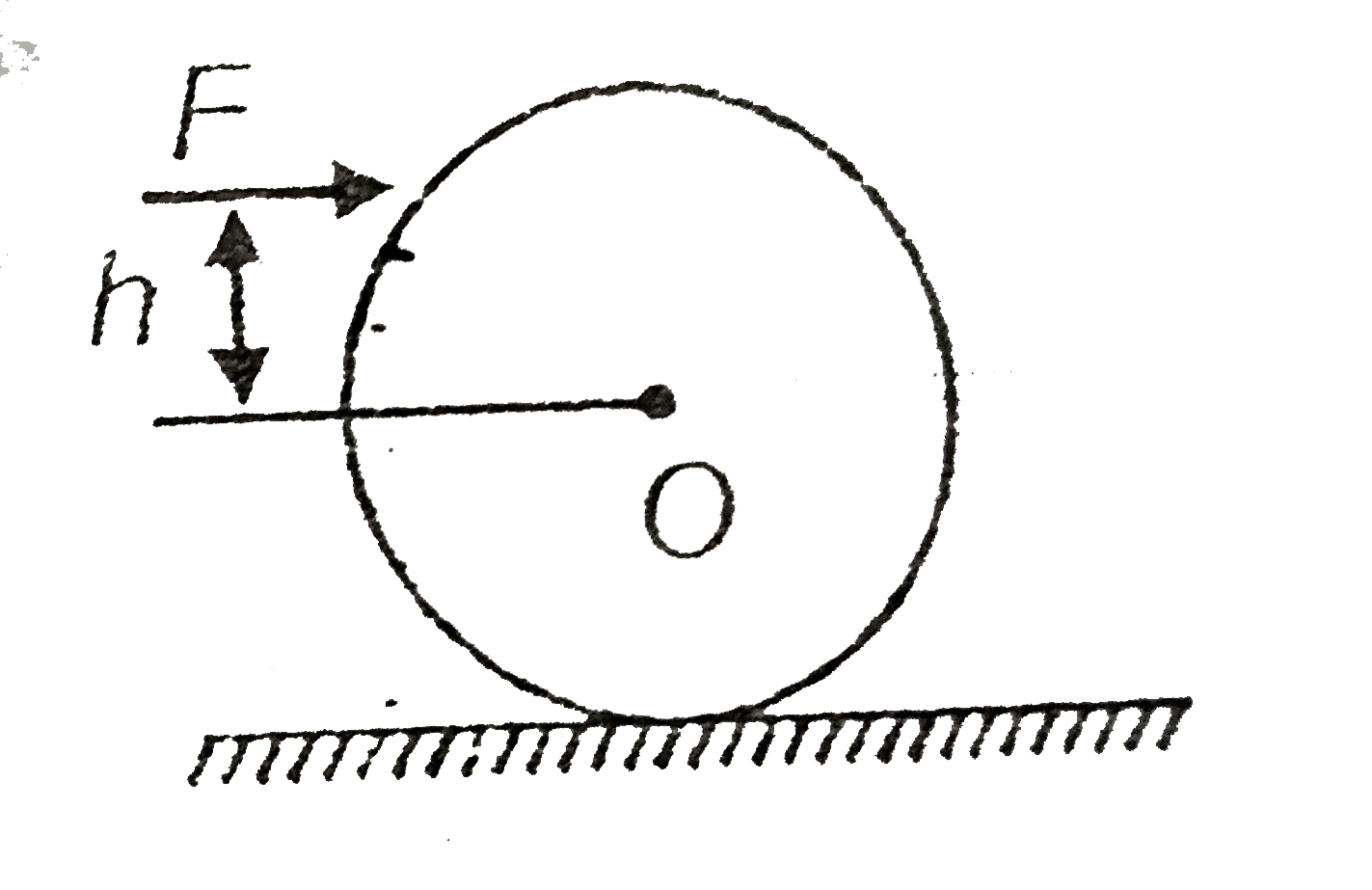
View SolutionA wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionThe drwing shows a bicycle wheel of radius r, resting against a small step whose height is h=r/5. A clockwise torque increases, there comes a time when the wheel just begins to rise up and loses contact with the ground. Let this torque be T. What is the magniitude of the horizontal component of the acceleration of the centre of the wheel when a torque of 2T is applied? Assume that the wheel doesn't slip at the edge of the step when this torque is applied (ignore the mass of the spokes).

View Solution
