A whistle is rotated in a horizontal circle. Is there any change in the sound of the whistle, heard by a person standing (i) at the centre of the circle (ii) outside the circle ?
To solve the problem, we need to analyze the situation for both observers: one at the center of the circle and the other outside the circle. We will use the principles of the Doppler effect to understand how the sound changes for each observer.
1. Understanding the Setup:
- A whistle (sound source) is rotating in a horizontal circle.
- We have two observers: one at the center of the circle and one outside the circle.
2. Case 1: Observer at the Center of the Circle:
- The observer is located at the center of the circle.
- The velocity of the whistle is always perpendicular to the line joining the whistle and the observer.
- According to the Doppler effect, if the component of the source's velocity along the line of sight to the observer is zero, the frequency heard by the observer remains the same as the actual frequency of the source.
- Conclusion for Case 1: There is no change in the frequency of the sound heard by the observer at the center of the circle.
3. Case 2: Observer Outside the Circle:
- The observer is located outside the circle.
- As the whistle rotates, the direction of the whistle's velocity changes, and at certain points, it will have a component of velocity directed towards or away from the observer.
- If we consider the angle θ between the line joining the whistle and the observer and the direction of the whistle's velocity, there will be a component of the velocity (V cos θ) along the line of sight.
- According to the Doppler effect, this component of velocity will affect the frequency heard by the observer. The apparent frequency will differ from the actual frequency of the source.
- Conclusion for Case 2: The frequency of the sound heard by the observer outside the circle will change due to the motion of the whistle.
Final Answers:
- (i) At the center of the circle: No change in frequency.
- (ii) Outside the circle: Change in frequency.
- A whistle (sound source) is rotating in a horizontal circle.
- We have two observers: one at the center of the circle and one outside the circle.
- The observer is located at the center of the circle.
- The velocity of the whistle is always perpendicular to the line joining the whistle and the observer.
- According to the Doppler effect, if the component of the source's velocity along the line of sight to the observer is zero, the frequency heard by the observer remains the same as the actual frequency of the source.
- Conclusion for Case 1: There is no change in the frequency of the sound heard by the observer at the center of the circle.
- The observer is located outside the circle.
- As the whistle rotates, the direction of the whistle's velocity changes, and at certain points, it will have a component of velocity directed towards or away from the observer.
- If we consider the angle θ between the line joining the whistle and the observer and the direction of the whistle's velocity, there will be a component of the velocity (V cos θ) along the line of sight.
- According to the Doppler effect, this component of velocity will affect the frequency heard by the observer. The apparent frequency will differ from the actual frequency of the source.
- Conclusion for Case 2: The frequency of the sound heard by the observer outside the circle will change due to the motion of the whistle.
- (i) At the center of the circle: No change in frequency.
- (ii) Outside the circle: Change in frequency.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - WAVESEXERCISE - Long Answer Questions16videos
WAVES
- BOOK - ICSECHAPTER - WAVESEXERCISE - Short Answer Questions.32videos
WAVES
- BOOK - ICSECHAPTER - WAVESEXERCISE - Musical Sound2videos
WAVES
- BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS79videos
VECTORS SCALARS ELEMENTARY CALCULUS
Similar Questions
A train approaching a hill at a speed of 40km/hr sounds a whistle of frequency 580Hz when it is at a distance of 1km from a hill. A wind with a speed of 40km/hr is blowing in the direction of motion of the train Find
(i) the frequency of the whistle as heard by an observer on the hill,
(ii) the distance from the hill at which the echo from the hill is heard by the driver and its frequency.
(Velocity of sound in air =1,200km/hr)View SolutionA train approaching a hill at a speed of 40km/hr sounds a whistle of frequency 580Hz when it is at a distance of 1km from a hill. A wind with a speed of 40km/hr is blowing in the direction of motion of the train Find
(i) the frequency of the whistle as heard by an observer on the hill,
(ii) the distance from the hill at which the echo from the hill is heard by the driver and its frequency.
(Velocity of sound in air =1,200km/hr)View Solution
Knowledge Check
- Question 1 - Select One
A railway engine passes by the platform at a speed of 36 km/hr blowing its whistle having a frequency of 660 Hz. The different in the frequencies of the whistle heard by a person standing on the platform as the engine goes past the person is equal to
AzeroB20 HzC40 HzD60 Hz
In figure, determine the measure of ∠QSR, where O I the centre of the circle.
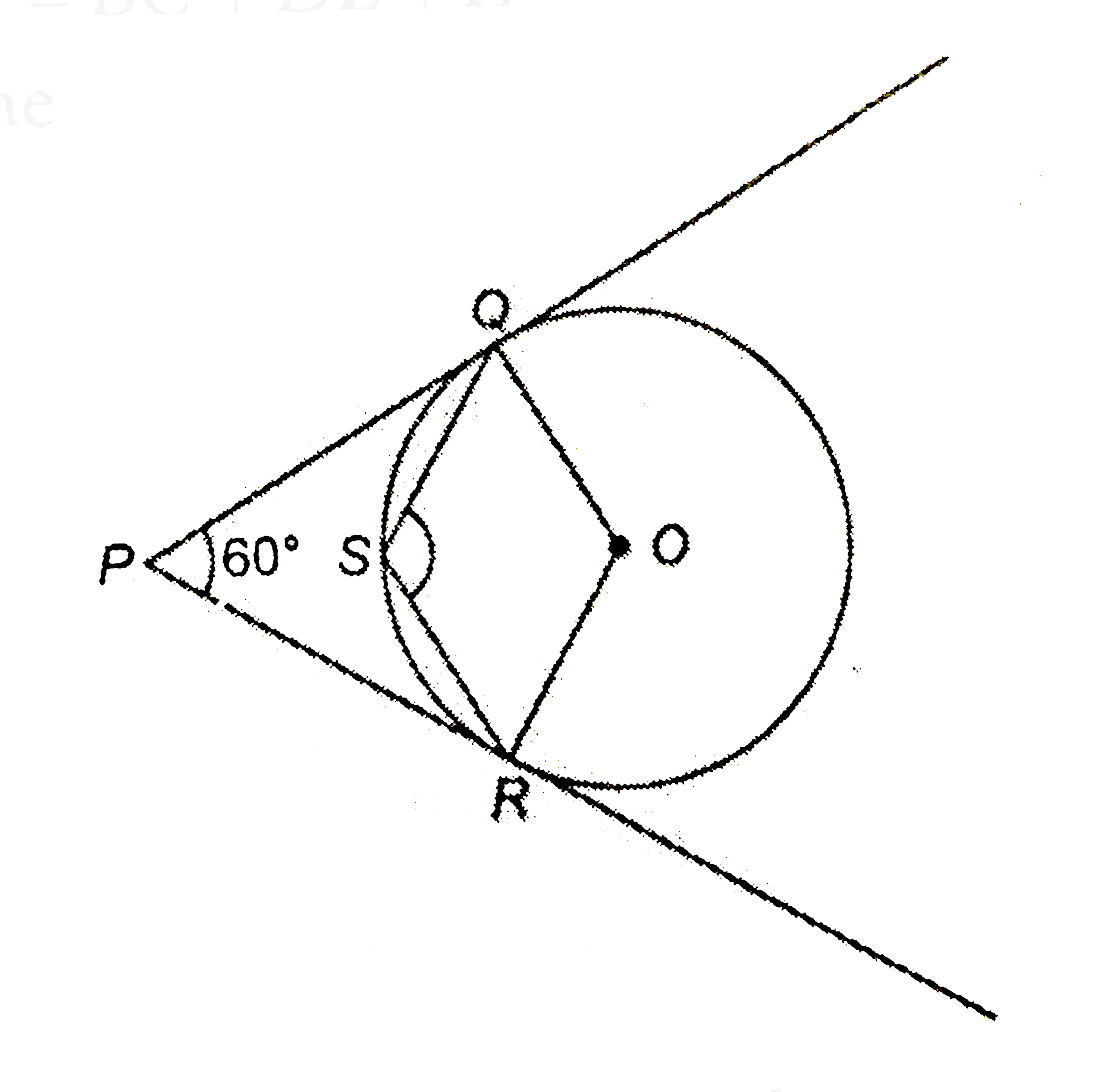 View Solution
View SolutionIn a circle of radius 6 cm, a chord of length 10 cm makes an angle of 110o at the centre of the circle. Find (i) the circumference of the circle, (ii) the area of the circle
View SolutionA particle is rotated in vertical circle by connecting it to string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionA particle is rotated in a verticle circle by connecting it to the end of massless rod of length l and keeping the other end of rod fixed. The minimum speed of the particle when the rod is horizontal for which the particle will complete the circle is
View SolutionA bullet passes past a person at a speed of 220ms−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air =330ms−1.
View SolutionDraw a circle of radius 4 cm. Take a poin P outside the circle. Without using the centre of the circle, draw two tangents to the circle from point P.
View SolutionA particle is rotated in verticla circle by connecting it to string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View Solution

