A whistle of frequency 500 Hz is rotated in a circle of radius cne metre with an angular speed of 10 radian/sec. Calculate the lowest and the highest frequency heard by a listener at a long distance away at rest with respect to the centre of the circle ? (Velocity of sound = 340m/s)
The correct Answer is:Lower =500×340/350=485.7Hz, Highest =500×340/340−10=515Hz.
To solve the problem of finding the lowest and highest frequency heard by a listener from a rotating whistle, we can follow these steps:
Step 1: Identify Given Values
- Frequency of the whistle (f) = 500 Hz
- Angular speed (ω) = 10 rad/s
- Radius of the circle (r) = 1 m
- Velocity of sound (v) = 340 m/s
Step 2: Calculate Linear Velocity of the Whistle
The linear velocity (Vs) of the whistle can be calculated using the formula:
Vs=ω×r
Substituting the values:
Vs=10rad/s×1m=10m/s
Step 3: Calculate Maximum Frequency (fmax)
The maximum frequency occurs when the source is approaching the observer. The formula for maximum frequency is:
fmax=f×v−v0v−Vs
Where:
- v0 (velocity of observer) = 0 (since the observer is at rest)
Substituting the values:
fmax=500×340−0340−10
fmax=500×340330
fmax=500×1.0303≈515.15Hz
Step 4: Calculate Minimum Frequency (fmin)
The minimum frequency occurs when the source is receding from the observer. The formula for minimum frequency is:
fmin=f×v−v0v+Vs
Substituting the values:
fmin=500×340−0340+10
fmin=500×340350
fmin=500×0.9714≈485.71Hz
Final Answers
- Highest frequency (fmax) = 515.15 Hz
- Lowest frequency (fmin) = 485.71 Hz
---
- Frequency of the whistle (f) = 500 Hz
- Angular speed (ω) = 10 rad/s
- Radius of the circle (r) = 1 m
- Velocity of sound (v) = 340 m/s
The linear velocity (Vs) of the whistle can be calculated using the formula:
Vs=ω×r
Substituting the values:
Vs=10rad/s×1m=10m/s
The maximum frequency occurs when the source is approaching the observer. The formula for maximum frequency is:
fmax=f×v−v0v−Vs
Where:
- v0 (velocity of observer) = 0 (since the observer is at rest)
fmax=500×340−0340−10
fmax=500×340330
fmax=500×1.0303≈515.15Hz
The minimum frequency occurs when the source is receding from the observer. The formula for minimum frequency is:
fmin=f×v−v0v+Vs
fmin=500×340−0340+10
fmin=500×340350
fmin=500×0.9714≈485.71Hz
- Highest frequency (fmax) = 515.15 Hz
- Lowest frequency (fmin) = 485.71 Hz
Topper's Solved these Questions
Similar Questions
A whitle of frequency 540 Hz rotates in a horizontal circle of radius 2 m at an angular speed of 15rads. What is the lowest and the highest frequency heard by a listener a long distance away at rest with respect to the centre of the circle? (Velocity of sound in air is c=330ms.)
View SolutionA whistle of frequency 540 Hz is moving in a circle of radius 2 ft at a constant angular speed of 15 rad/s. What are the lowest and highest frequencies heard by a listener standing at rest, a long distance away from the centre of the circle? (Velocity of sound in air is 1100ft/s)
View SolutionA whistle of frequency 540HZ rotates in a circle of radius 2mat a linear speed of 30m/s . What is the lowest and highest frequency heard by an observer a long distance away at rest with respect to the centre of circle ? Take speed of sound of sound in air as 330m/s. Can the apparent frequency be ever equal to actual ?
View SolutionA whistle emitting a sound of frequency 440Hz is tied to a string of 1.5m length and roated with an angular velocity of 20rad/s in the horizontal plane. Calculate the range of frequencies heard by an observer stationed at a larger distance from the whistle .(Speed of sound =330m/s) .
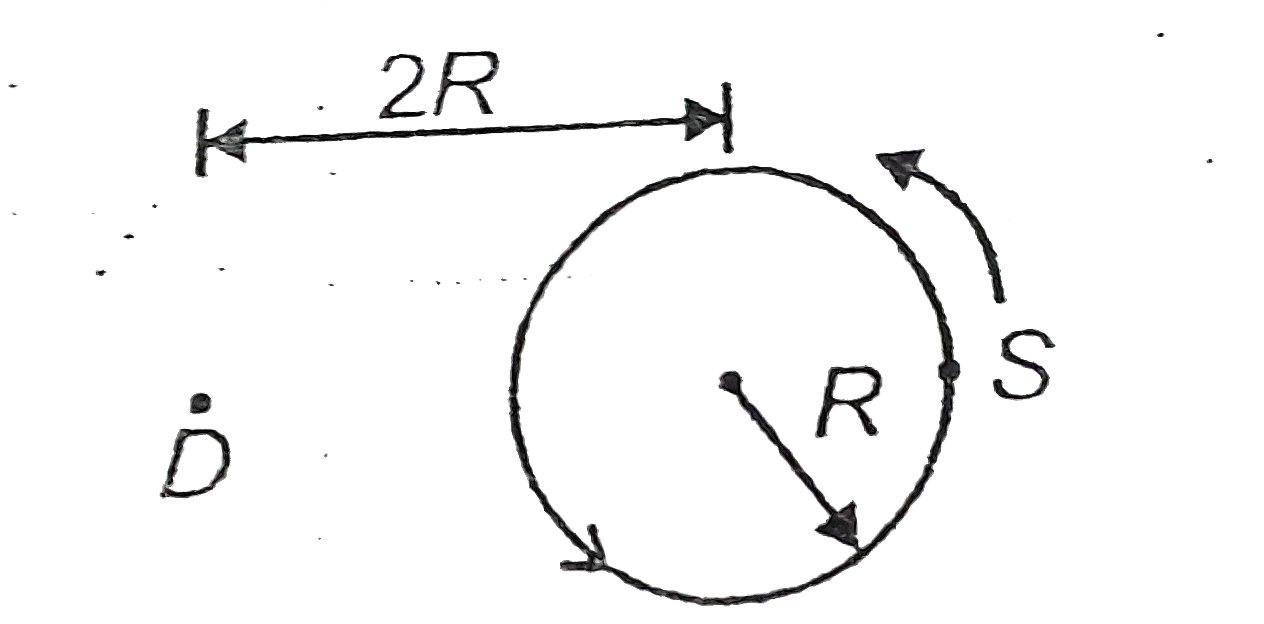
View SolutionA whistle 'S' of frequency v revolves in a circle of radius R at a constant speed v. what is the ratio of the largest and smallest frequency detected by a detector D, at rest, at a distance 2 R from the centre of the circle as shown in the figure? (take speed of sound in air as c)
 View Solution
View SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer who is at rest at a great distance from the centre of the circle but nearly in the same plane, the minimum fmin and the maximum fmax of the range of values of the apparent frequency heard by him will beView SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer who is at rest at a great distance from the centre of the circle but nearly in the same plane, the minimum fmin and the maximum fmax of the range of values of the apparent frequency heard by him will beView SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer situated at a great distance on a straight line perpendicular to the plane of the circle, through its centre, the apparent frequency of the source will beView SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer situated at a great distance on a straight line perpendicular to the plane of the circle, through its centre, the apparent frequency of the source will beView SolutionA car moving with a speed of 30ms−1 is approaching a factory whistle having the frequency 700 Hz. Calculate the apparent pitch of the whistle as heard by the driver of the car ? (Velocity of sound = 350m/s)
View Solution

