A whistle revolves in a circle with an angular speed of using a string of length . If the frequency of sound from the whistle is , then what is the minimum frequency heard by an observer which is far away from the centre in the same plane?
The correct Answer is:B
To solve the problem, we need to determine the minimum frequency heard by an observer when a whistle is revolving in a circle. We will use the Doppler effect formula for sound.
Given Data:
- Angular speed, ω=20rad/s
- Length of string (radius), r=50cm=0.5m
- Frequency of sound from the whistle, f0=385Hz
- Speed of sound, v=340m/s
1. Calculate the linear speed of the whistle (source):
The linear speed vs of the whistle can be calculated using the formula:
vs=r⋅ω
Substituting the values:
vs=0.5m⋅20rad/s=10m/s
2. Identify the observer's position:
The observer is positioned far away from the center of the circle, in the same plane as the whistle. Since the whistle is moving away from the observer at the point of minimum frequency, we will use the Doppler effect formula for a source moving away from a stationary observer.
3. Apply the Doppler effect formula:
The formula for the frequency heard by the observer when the source is moving away is given by:
f′=f0⋅vv+vs
Where:
- f′ is the frequency heard by the observer,
- f0 is the emitted frequency,
- v is the speed of sound,
- vs is the speed of the source.
4. Substituting the values:
Now, substitute the known values into the formula:
f′=385Hz⋅340m/s340m/s+10m/s
f′=385Hz⋅340350
5. Calculating the frequency:
Now calculate the fraction:
f′=385Hz⋅3435
f′=385Hz⋅0.9714≈374Hz
Final Answer:
The minimum frequency heard by the observer is approximately 374Hz.
---
- Angular speed, ω=20rad/s
- Length of string (radius), r=50cm=0.5m
- Frequency of sound from the whistle, f0=385Hz
- Speed of sound, v=340m/s
The linear speed vs of the whistle can be calculated using the formula:
vs=r⋅ω
Substituting the values:
vs=0.5m⋅20rad/s=10m/s
The observer is positioned far away from the center of the circle, in the same plane as the whistle. Since the whistle is moving away from the observer at the point of minimum frequency, we will use the Doppler effect formula for a source moving away from a stationary observer.
The formula for the frequency heard by the observer when the source is moving away is given by:
f′=f0⋅vv+vs
Where:
- f′ is the frequency heard by the observer,
- f0 is the emitted frequency,
- v is the speed of sound,
- vs is the speed of the source.
Now, substitute the known values into the formula:
f′=385Hz⋅340m/s340m/s+10m/s
f′=385Hz⋅340350
Now calculate the fraction:
f′=385Hz⋅3435
f′=385Hz⋅0.9714≈374Hz
The minimum frequency heard by the observer is approximately 374Hz.
Topper's Solved these Questions
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - AIIMS Questions
55 Videos
- VECTORSBOOK - A2ZCHAPTER - VECTORSEXERCISE - Chapter Test
29 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test
29 Videos
Similar Questions
(i) What is beat phenomenon?
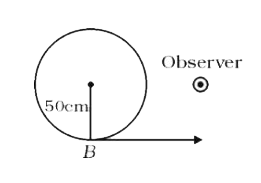
(ii) A whistle revolves in a circle with angular velocity of ω=20rads−1. If the frequency of sound is 385 Hz and speed is 340 ms−1, then find the frequency heard by the observer when the whistle is at B.
View SolutionAn observer and a source both are moving away with velocity 20 m/s each in opposite direction. If frequency of sound observed is 1800Hz then what is actual frequency (velocity of sound= 340 m/s)
View Solution
Knowledge Check
A whistle revolves in a circle with angular speed 0 = 20 rad/sec using a string of length 50 cm. If the frequency of sound from the whistle is 385 Hz, then what is the minimum frequency heard by an observer which is far away from the centre? (velocity of sound = 340 m/s)
A385 HzB374 HzC394 HzD333 HzA whistle revolves in a circle with an angular speed of 20rad/sec using a string of length 50cm. If the frequency of sound from the whistle is 385Hz, then what is the minimum frequency heard by an observer which is far away from the centre in the same plane? v=340m/s
A385 HzB374 HzC394 HzD333 HzA source of sound is rotating in the anticlockwise direction on a circle of radius 3 m, with an angular velocity of 10 rad s−1, given the frequency of the sound produced is 340 Hz and the velocity of sound is 330m s−1. The maximum frequency heard by the observer in the plane of the circle at a large distance will be
 A300 HzB374 HzC474 HzDnone of these
A300 HzB374 HzC474 HzDnone of these
A disc of radius R is rotating uniformly with angular frequency . A source of sound is fixed to the rim of the disc. The ratio of maximum to minimum frequency heard by a stationary observer, far away from the disc and in the plane of the disc is: (v = speed of sound)
View SolutionWhen a siren of a fire engine approaches an observer at a speed of 10m s−1, taking the velocity of sound is 340m s−1, if the frequency of the siren is 600 Hz, the frequency heard by the observer is
View SolutionA whistle emitting a loud sound of frequency 540 Hz is whirled in a horizontal circle of radius 2 m and at a constant angular speed of 15rad/s. The speed of sound is 330m/s. The ratio of the highest to the lowest frequency heard by a listener standing at rest at a large distance from the center of the circle is
View SolutionA train approaching a railway platform with a speed of 20 m s−1 starts blowing the whistle. Speed of sound in air is 340 ms−1. If the frequency of the emitted sound from the whistle is 640 Hz, the frequency of sound as heard by person standing on the platform
View Solution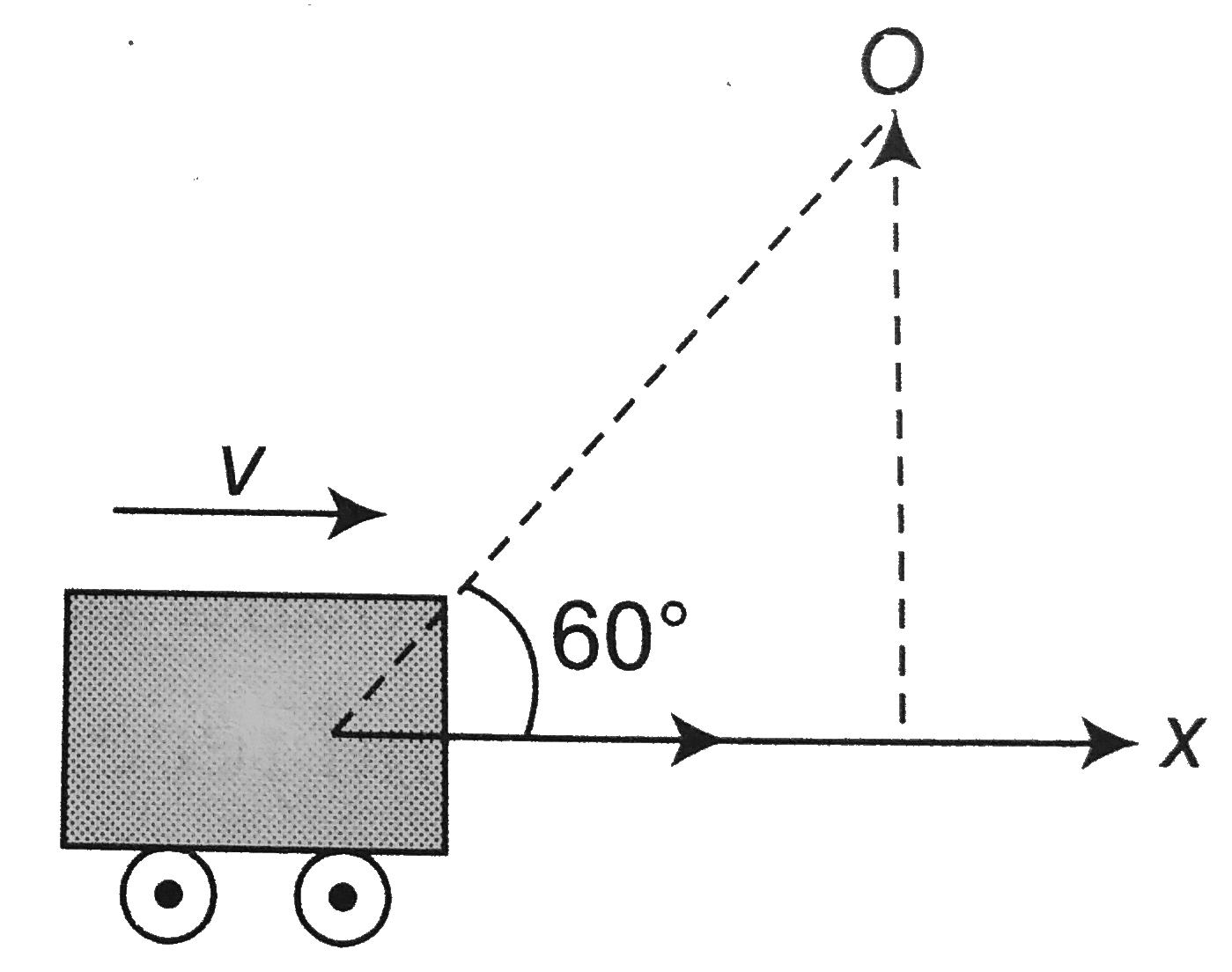
A car is moving along X-axis with a velocity v=20m/s. It sounds a whistle of frequency 660 Hz. If the speed of sound is 340m/s. The apparent frequency heard by the observer O (shown in figure) is:
View Solution
