(a) Why do the 'free electrons' , in a metal wire , flowing by themselves' not cause any current flow in the wire ?
Define drift velocity' and obtain an expression for the current flowing in a wire, in terms of the 'drift velocity of the free electrons.
(b) Use the above expression to show that the 'resistivity ' of the material of a wire is inversely proportional to the 'relaxation time' for the 'free electrons ' in the metal.
At room temperature, free electrons move with velocities of the order of 105ms−1. However , these velocities are distributed randomly in all directions. There is no preferred direction of motion. On the average, number of electrons travelling in any direction will be equal to number of electrons travelling in the opposite direction. If →u1,→u2,....→uN are the randsom velocities of N free electrons, then average velocity of electrons will be →u=→u1+→u2+......→uNN=0.
It may be defined as the average velocity gained by the free electrons of a conductor in the opposite direction of the externally applied electric field.
Suppose a potential difference V is applied across a conductor of length l and of uniform cross-section A. The electric field E set up inside the conductor is given by
E=VI
Let the number of electrons per unit volume of electron density =n
Change on an electron =e
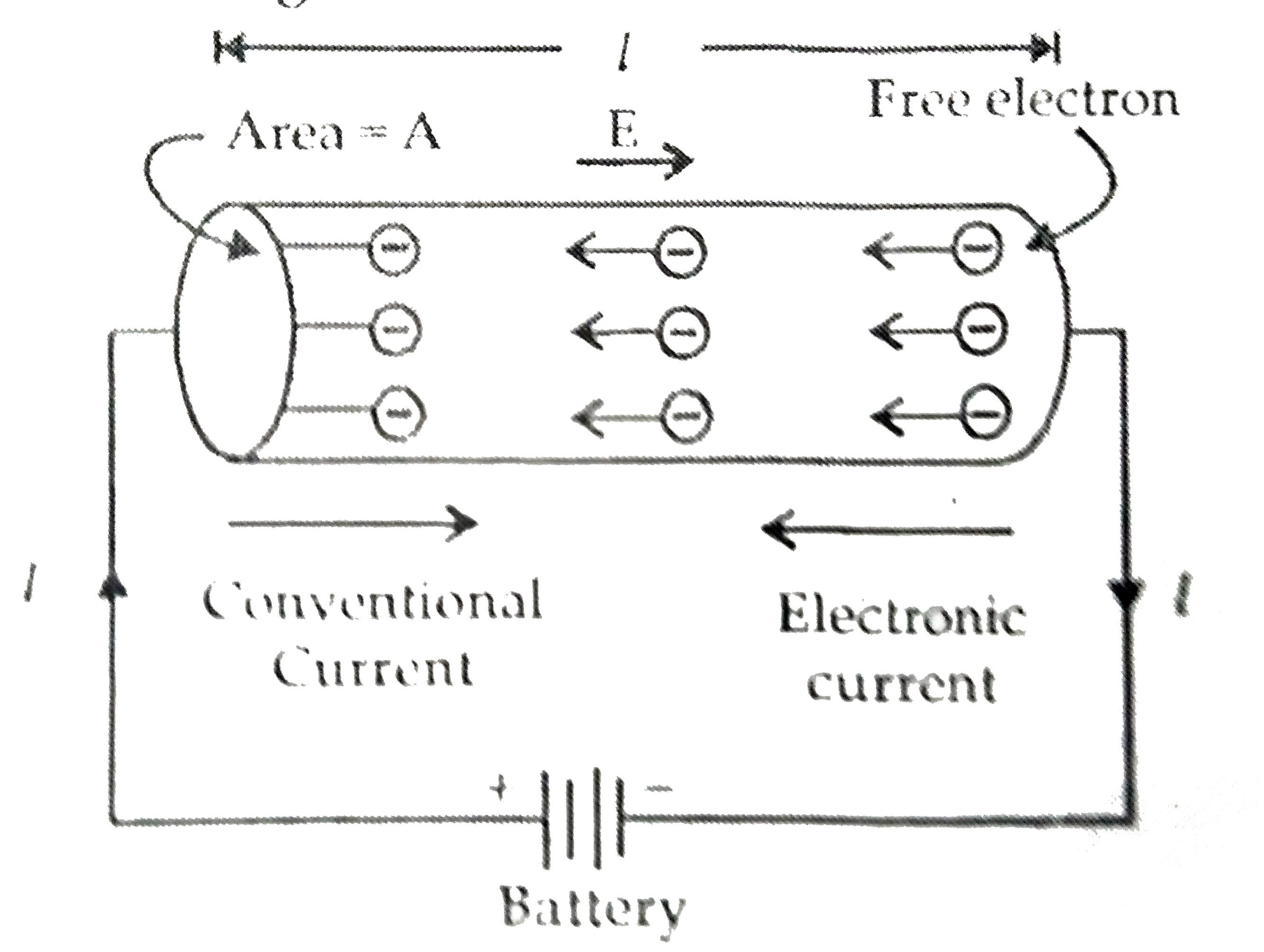
(b) Number of electrons in length l of the conductor
n× volume of the conductor is
Total charge contained in length l of the conductor is
q= en Al
All the electrons which enter the conductor at the right end will pass through the conductor at the left end in time,
t=distancevelocity=lυd
∴ CurrentI=qt=enAll/εdorI=enAvd
or VI=ml≠2τA
At a fixed temperautre , the quantities m,l,e,τ,andA, all have constant values for a given conductor.
Therefore ,
VI= a constant, R
This proves Ohm's law for a conductor and here R=ml≠2τA is the resistance of the conductor.
Resistivity in terms of electron density and relaxation time. The resistance R of a conductor of length l, area of cross-section A and resistivity ρ is given by R=ρlA.
But R=ml≠2τA
where, τ is the relaxation time.
Comparing the above two equations, we get
ρ=m≠2τ.
Similar Questions
When current flows through a conductor, then the order of drift velocity of electrons will be
View SolutionDefine relaxation time of the free electrons drifting in conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
View SolutionExplain the term 'drift velocity' of electrons in a conductor. Hence obtain the expression for the current through a conductor in terms of 'drift velocity'.
View SolutionThe magnetic field at the origin due to the current flowing in the wire is
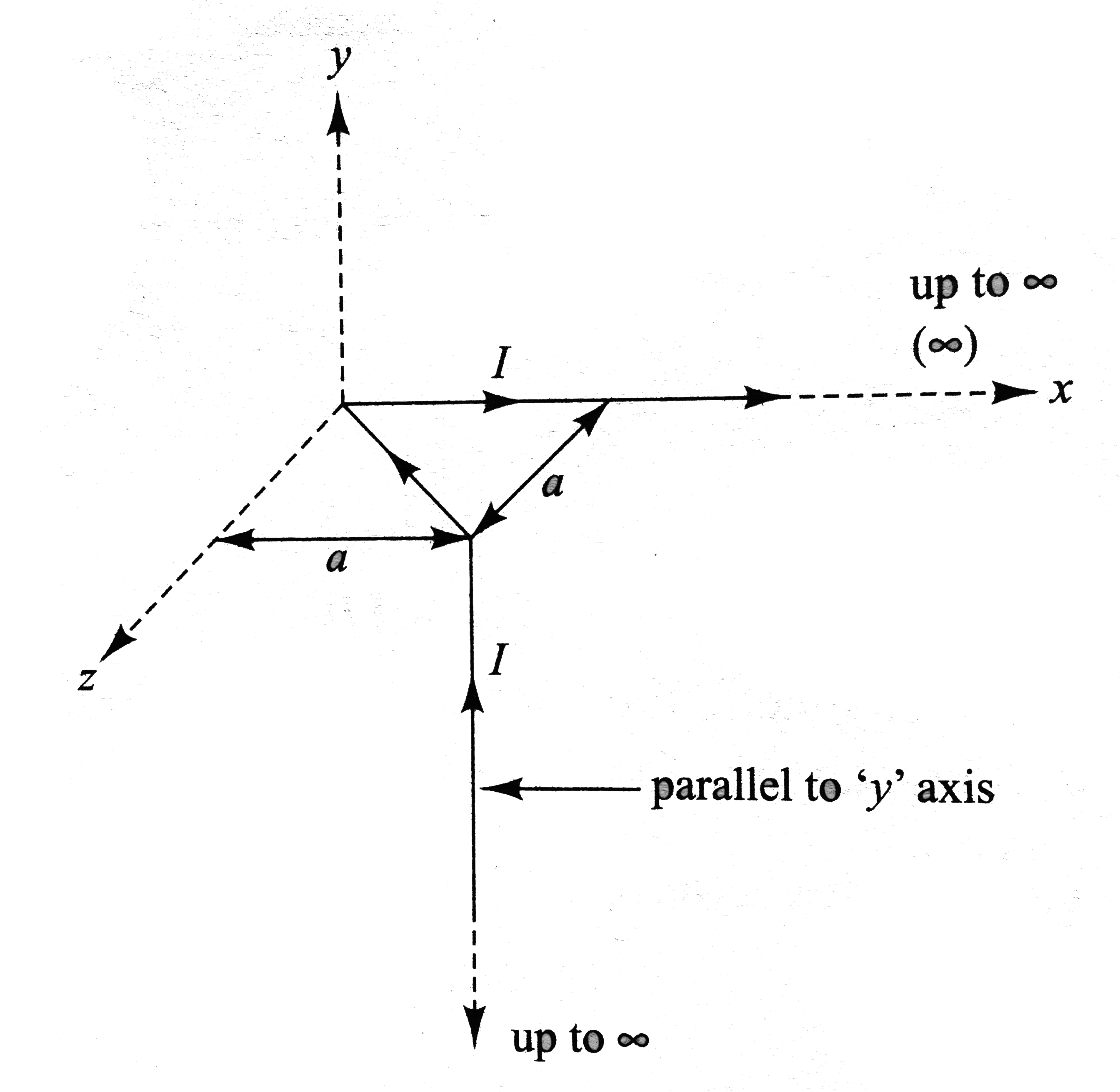
View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionDefine drift velocity and relaxation time, with reference to the free electron theory of conductors.
View SolutionThe electric current flowing in a wire in the direction from B to A decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown.

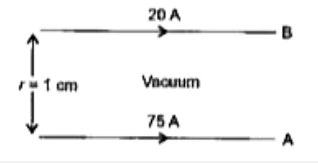
View SolutionCalculate force per unit length acting on the wire B due to the current flowing in the wire A. (see figure below)
View SolutionDefine drift velocity of free electron . If relaxation time is r then write a vector relation b etween drift velocity and electric field.
View SolutionDefine the term 'drift velocity' of electrons in a current carrying conductor. Obtain the relationship between the current density and the drift velocity of electrons.
View Solution
