A wire carrying current i has the configuration as shown in figure. Two semi-infinite straight sections, both tangent to the same circle, are connected by a circular arc of central angle theta, along the circumference of the circle, with all sections lying in the same plane. What must θ (in rad) be in order for B to be zero at the centre of the circle?
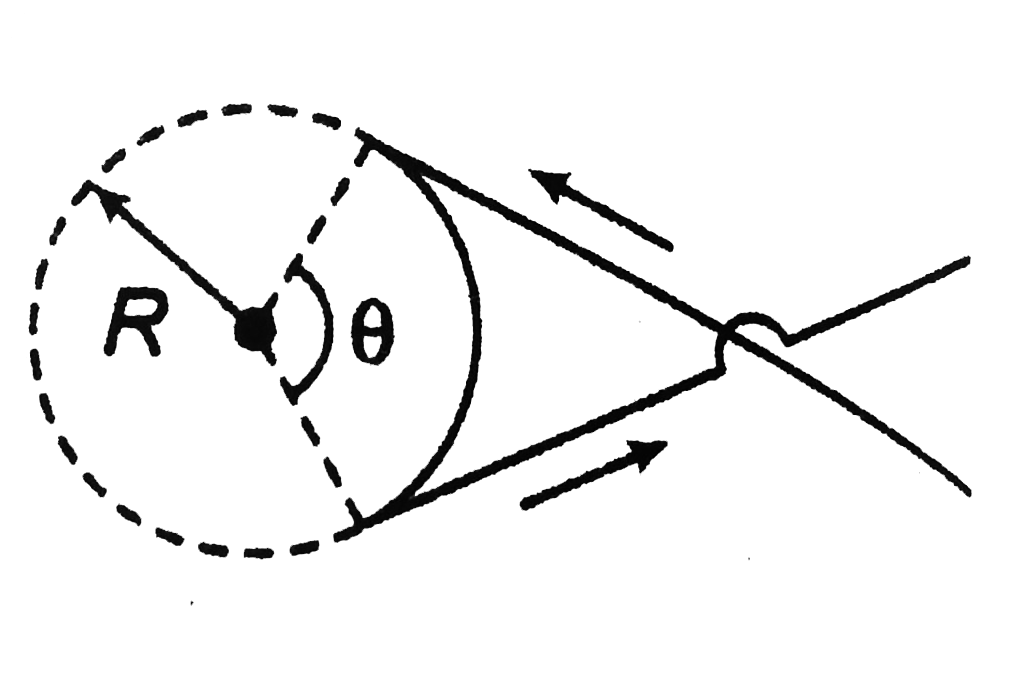
The correct Answer is:2
(2) Magnetic field at O due to wire 1 is,
→B1=μ0i4πR⊙
and that due to wire 2 is
→B2=μ0i4πR⊙⇒→B=→B1+→B2=μ0i2πR⊙

Magnetic field at the centre due to circular are subtending angle
θ at the centre is given by
→Barc=μ0i2R(θ2π)⊗
If →Bnet=0⇒→B+→Barc=0
⇒→B=−→Barc
⇒μ0i2πR⊙=−μ0i2R(θ2π)⊗
⇒μ0i2πR=μ0i2R(θ2π)=1π=θ2π⇒θ=2rad
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Archives (fill In The Blanks)
Explore 1 Video
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Archives (single Correct Anser)
Explore 13 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (linked Comprehension)
Explore 21 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:CENGAGE PHYSICSChapter:SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:QUESTION BANK
Explore 12 Videos
- THERMAL PROPERTIES OF MATTERBook:CENGAGE PHYSICSChapter:THERMAL PROPERTIES OF MATTERExercise:Question Bank
Explore 40 Videos
Similar Questions
A wire carrying current i has the configuration as shown in figure. Two semi-infinite straight sections, both tangent to the same circle, are connected by a circular arc of central angle theta, along the circumference of the circle, with all sections lying in the same plane. What must be for B to be zero at the centre of the circle?

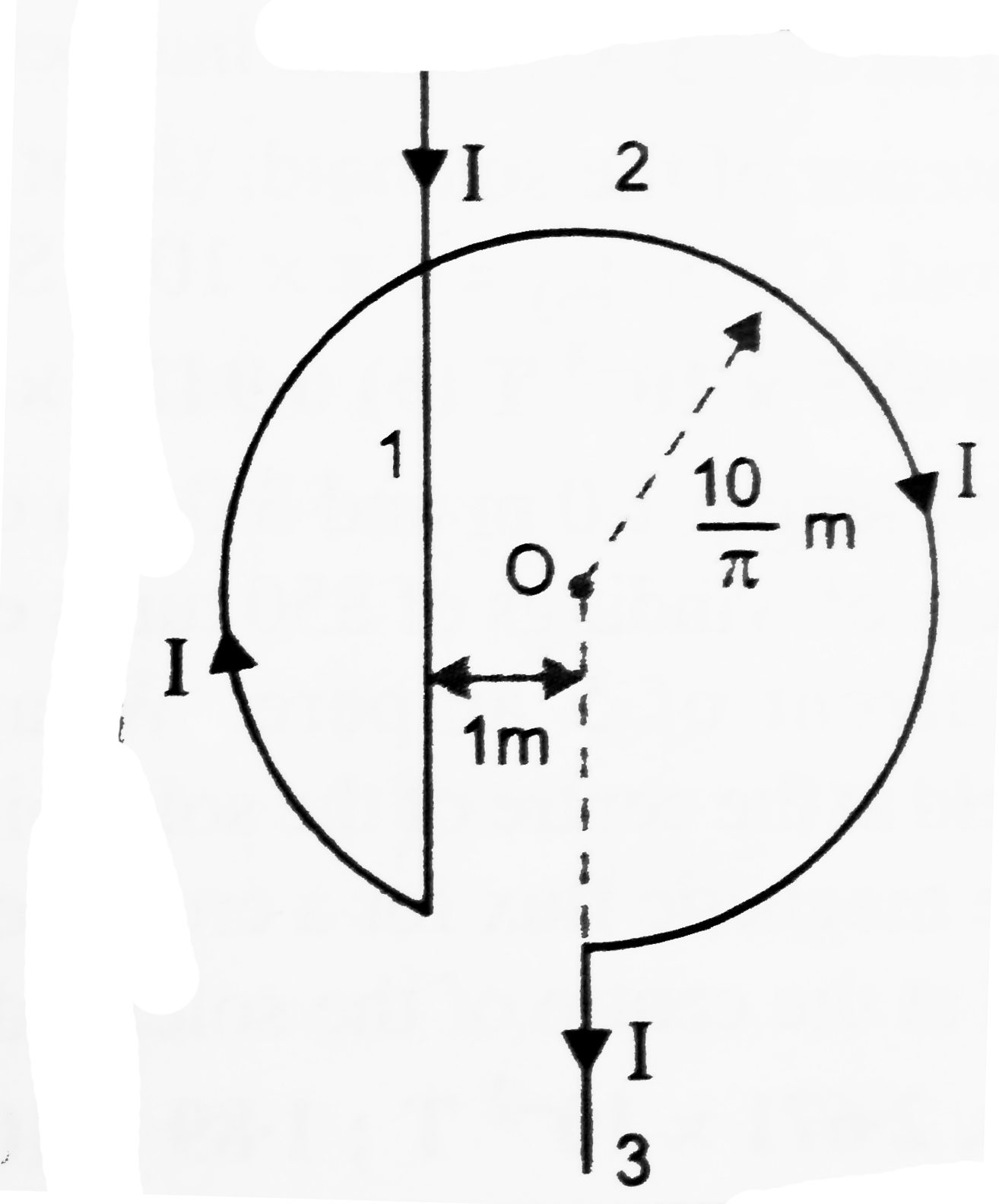
View SolutionA long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius (10/π)m. The centre of this circle is at a distance 1m from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given π2=10.
View Solution
Knowledge Check
Figure. Shows a small loop carrying a current I. The curved portion is an arc of a circle of radius R and the straight portion is a chord to the same circle subtending an angle θ. The magnetic induction at centor O is
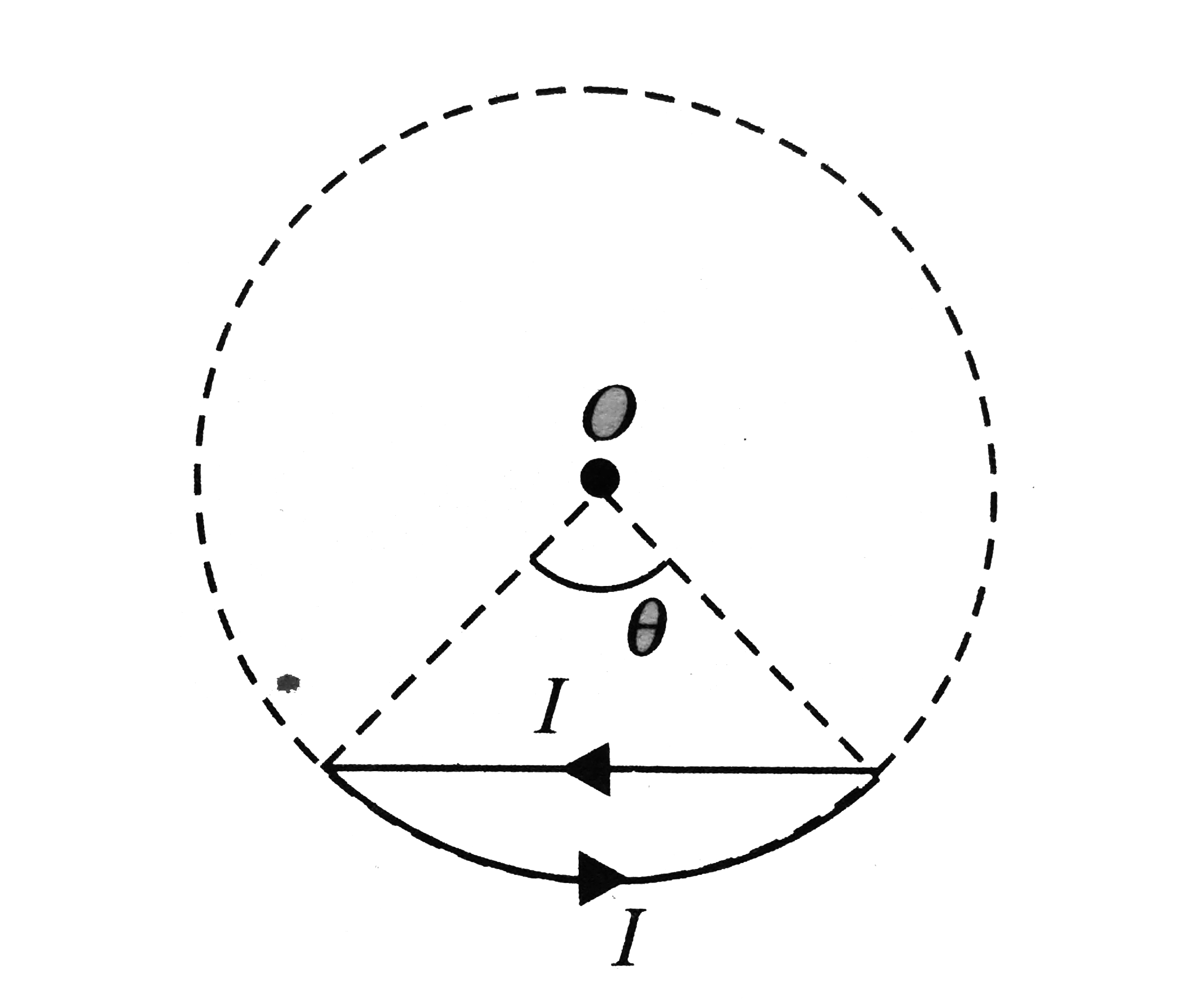 AzeroBalways inward irrespective of the value θCinward as long as θ is less than πDalways outward irrespective of the value of θ
AzeroBalways inward irrespective of the value θCinward as long as θ is less than πDalways outward irrespective of the value of θTwo long straight wires are connected by a circular section which has a radius R. All the three segments lie in the same plane and carry a current I. The magnetic induction at the centre O of the circular segments is
 Aμ0I4πRBαμ0I4πRCαμ0IRDαμ0I2πR
Aμ0I4πRBαμ0I4πRCαμ0IRDαμ0I2πRA wire carrying a current I is bent into the shape of an exponential spiral, r=eθ, from θ=0 to θ=2π as shown in figure (a0 . To complete a loop, the ends of the spiral are connected by a straight wire along the x− axis. Find the magnitude and direction of →B at the origin.
 Aμ0I4π(1−e−2π)Bμ0I3π(1−e−2π)Cμ0Iπ(1−e−2π)Dμ0I2π(1−e−2π)
Aμ0I4π(1−e−2π)Bμ0I3π(1−e−2π)Cμ0Iπ(1−e−2π)Dμ0I2π(1−e−2π)
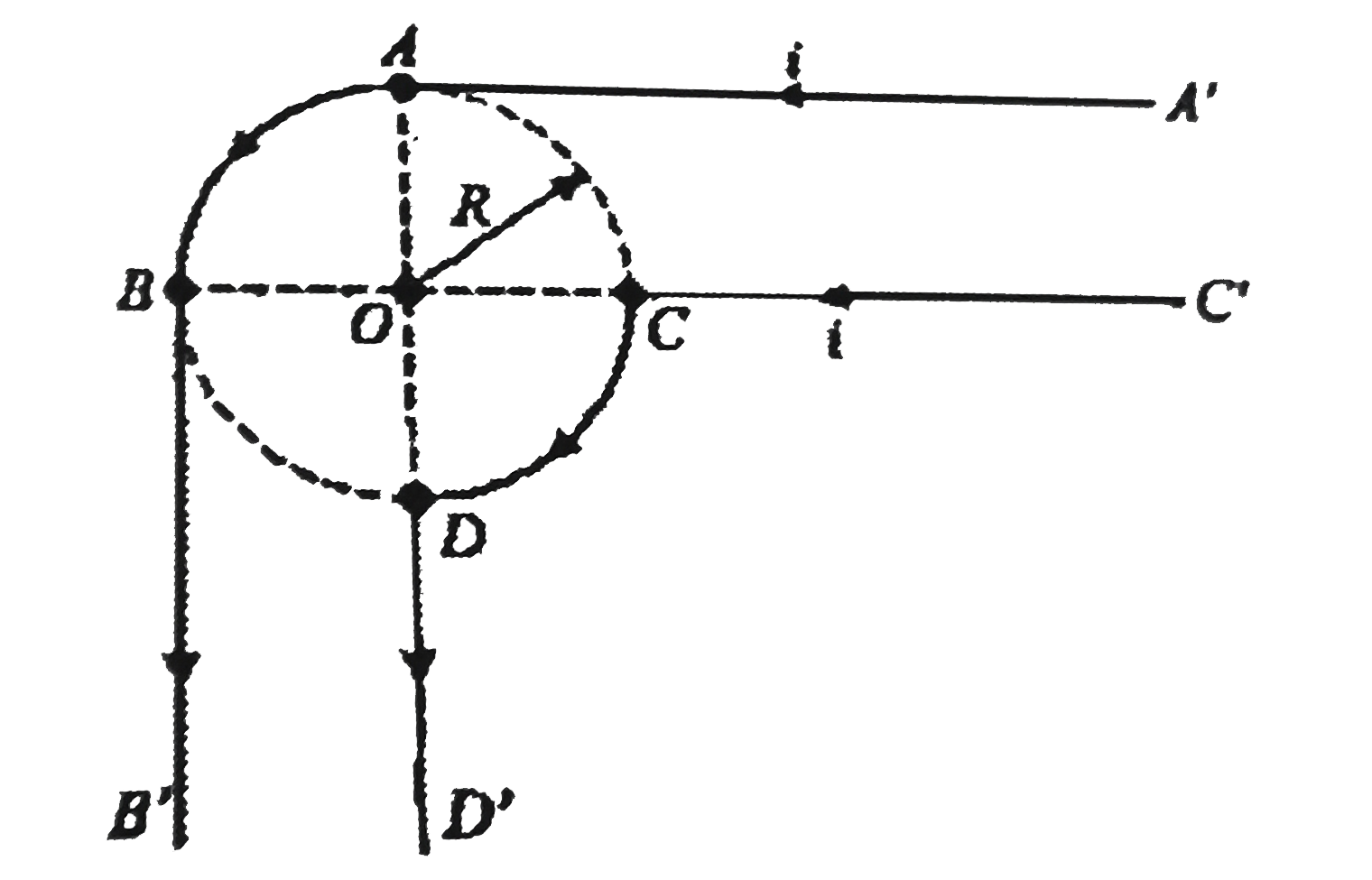
The configuration of some current carrying wires is shown in figure-4.217. All straight wires are very long. Both AB and CD are arcs of the same circle, both subtending right angles at the centre 0. The magnetic field at O is:
View SolutionTwo fixed long straight wires carry the same current i in opposite directions as shown in . A square loop of side b is fixed in the plane of the wires with its length parallel to one wire at a distance a shown in the figure.

(a) alculate at the induced emf in the loop if the current in both the wires is changing at the rate di/dt.
(b) What is the direction of force on the loop if di/dt is positive?
View SolutionIn the shown figure a current 2i is flowing in a straight conductor and entering along the diameter of the circular loop of similar conductor through the point A. The current is leaving the loop along another similar semi-infinite conductor parallel to the plane of the loop through the point D. what is the magnetic field at the centre of the loop P ?
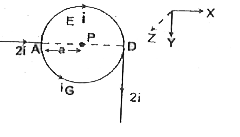
View SolutionA current of 10A flows around a closed path in a circuit which is int eh horizontal plne as shown in the figure. The circuit consists oif eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
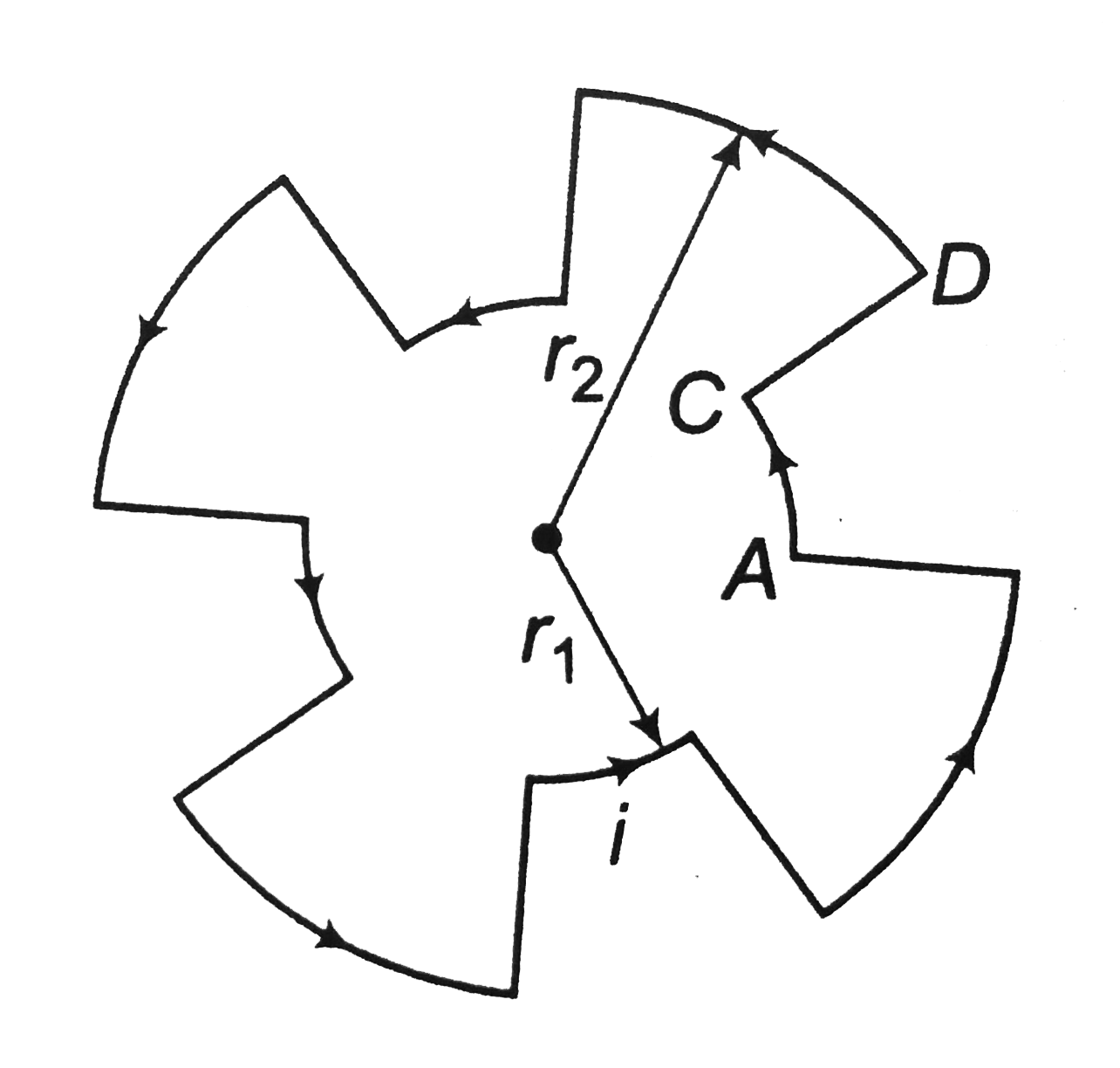
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carryin as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centredue to the curren in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
View SolutionThe wire shown in Fig. carries current I in the direction shown. The wire consists of a very long, straight section, a quarter- circle with radius R, and another long, straight section. What are magnitude and direction of net magnetic field at the center of curvature of quarter-circle section (point P)?

View Solution