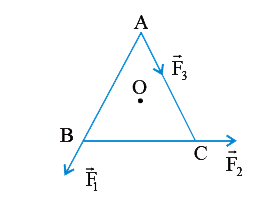
ABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is

F1+F22
2(F1+F2)
F1+F2
F1−F2
The correct Answer is:C
Taking anticlockwise torque
F1d+F2d−F3d=0 (where d= perpendicular distance of the centre O from each side)
∴F3=F1+F2
Topper's Solved these Questions
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - QUESTION
95 Videos
- MOTION IN TWO AND THREE DIMENSIONBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - MOTION IN TWO AND THREE DIMENSIONEXERCISE - All Questions
47 Videos
- NEET 2020BOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEET 2020EXERCISE - All Questions
45 Videos
Similar Questions
ABC is an equilateral with O as its centre →F1,→F2 and →F3 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of →F3 is :
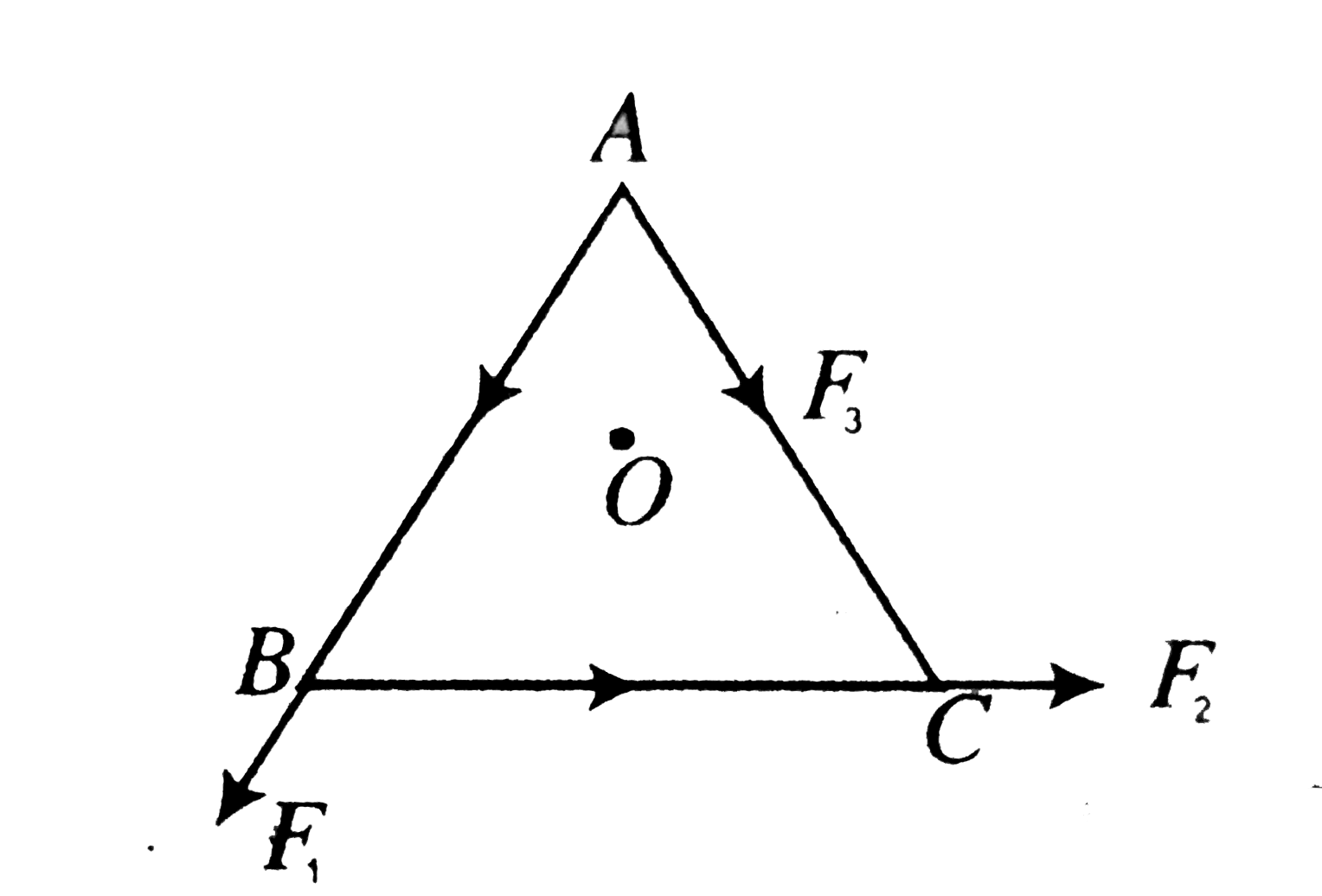
View SolutionO is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
View Solution
Knowledge Check
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
 A2(F1+F2)BF1+F22CF1−F2DF1+F2
A2(F1+F2)BF1+F22CF1−F2DF1+F2O is the centre of an equilateral triangle ABC. F1,F2 and F3 are three forces acting along the sides AB, BC and AC as shown in the figure. What should be the magnitude of F3, so that the total torque about O is
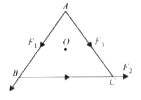 A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)
A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)In a triangle ABC three forces of magnitudes 3−−→AB,2−−→AC and 6−−→CB are acting along the sides AB, AC and CB respectively . If the resultant meets AC at D, then the ratio DC: AD will be equal to
A1:1B1:2C1:3D1:4
Let →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
View SolutionIf D, E, F are the mid points of the side BC, CA and AB respectively of a triangle ABC, write the value of →AD+→BE+→CF.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC and G is the centroid of the triangle, then −−→GD+−−→GE+−−→GF=
View SolutionABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
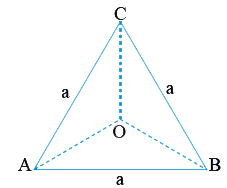
−−→AB+−−→BC+−−→CA
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC and G is the centroid of the triangle, then −−→GD+−−→GE+−−→GF=
View Solution
