ABCD is parallelogram $\to A, \to B, \to C and \to D$ are the position vectors of vecticles A, B, C, and D with respect to any origin, them:

A

$\to A + \to B = \to C - \to D$

B

$\to C - \to B = \to A + \to D$

C

$\to B - \to C = \to A - \to D$

D

$\to A + \to B + \to C + \to D = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$\to A \to B + \to C \to D = 0$
$(\to B - \to A) + \to D - \to C = 0$
Sum of opposite sides = zero

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

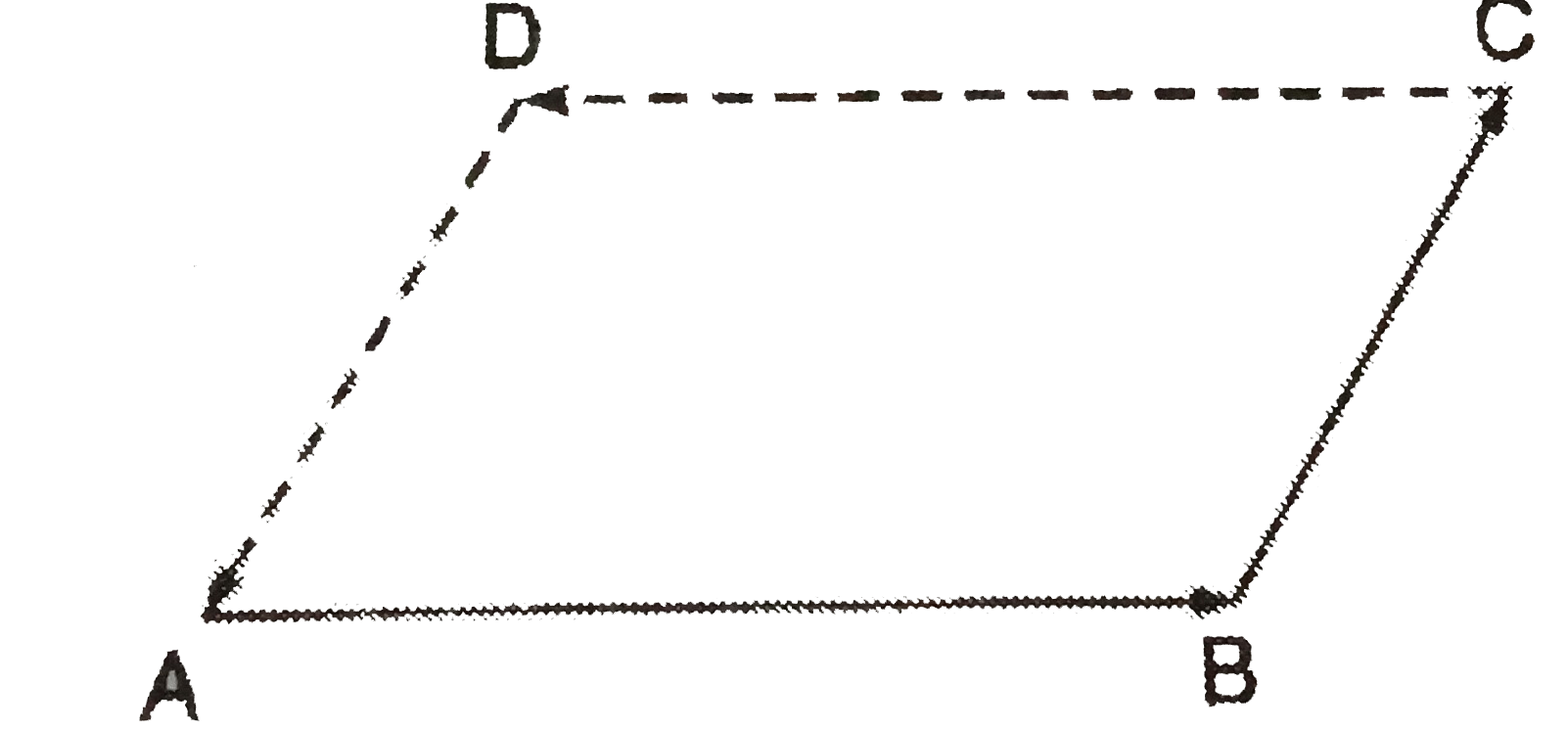
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let the position vectors of vertices $A, B, C$ of $Δ A B C$ be respectively $\to a, \to b$ and $\to c$ . If $\to r$ is the position vector of the mid point of the line segment joining its orthocentre and centroid then $(\to a - \to r) + (\to b - \to r) + (\to c - \to r) =$
A1
B2
C3
Dnone of these
Question 2 - Select One
If $\to A \times \to B = \to C + \to D$ , them select the correct alternative:
A $\to B$ is parallel to $\to C + \to D$
B $\to A$ is perpendicular to $\to C$
CComponent of $\to C$ along $\to A$ = Components of $\to D$ along $\to A$
DComponent of $\to C$ along $\to A$ =-Components of $\to D$ along $\to A$
Question 3 - Select One
A, B, C and D have position vectors $\to a, \to b, \to c and \to d$ , repectively, such that $\to a - \to b = 2 (\to d - \to c)$ . Then
AAB and CD bisect each other
BBD and AC bisect each other
CAB and CD trisect each other
DBD and AC trisect each other

GRB PUBLICATION-VECTORS-OBJECTIVE QUESTIONS

Home
Ask Doubt
Profile