According to Kepler, the period of revolution of a planet ( T ) and its mean distance from the sun ( r ) are related by the equation

A

$T^{2} r$ = Constant

B

$T^{2} r^{- 3} =$ Constant

C

$T^{2} r^{3} = Constant$

D

$T^{3} r^{3} =$ Constant

Video Solution

Text Solution

Verified by Experts

The correct Answer is:b

$T^{2} = \frac{4 π^{2}}{G M} r^{3}$
$\frac{T^{2}}{T^{3}} = \frac{4 π^{2}}{G M} = constant$
$T^{2} r^{- 3} = constant.$

|

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time $t_{1}$ and $l_{2}$ in moving from $A$ to $B$ and from $C$ to $D$ respectively, then

A $\frac{3 G M m}{a}$
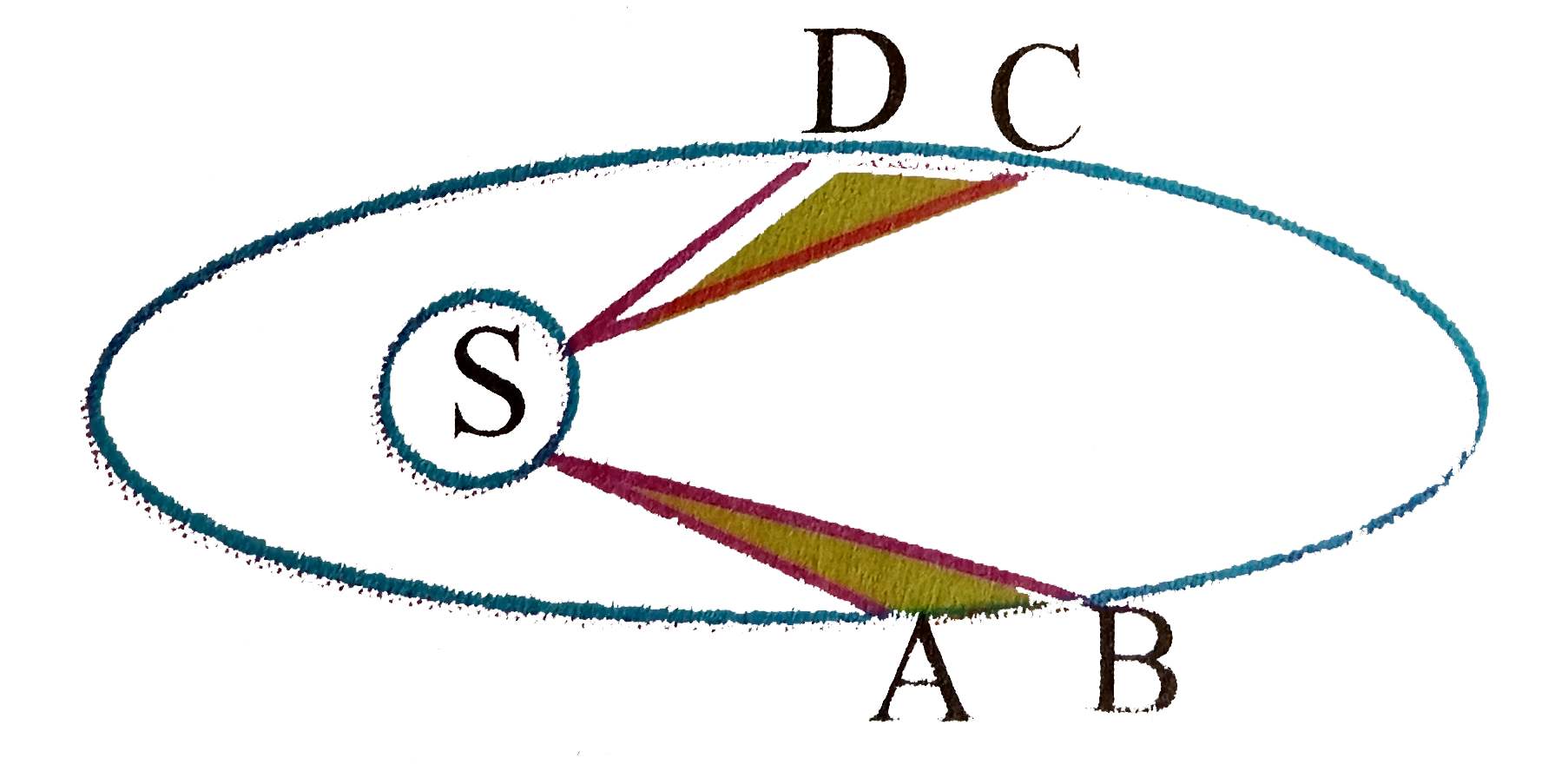B $\frac{5 G M m}{a}$
C $\frac{G M m}{a}$
Dnone of the above
Question 2 - Select One
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time $t_{1}$ and $l_{2}$ in moving from $A$ to $B$ and from $C$ to $D$ respectively, then

A $- \frac{3 G M m}{4 a}$
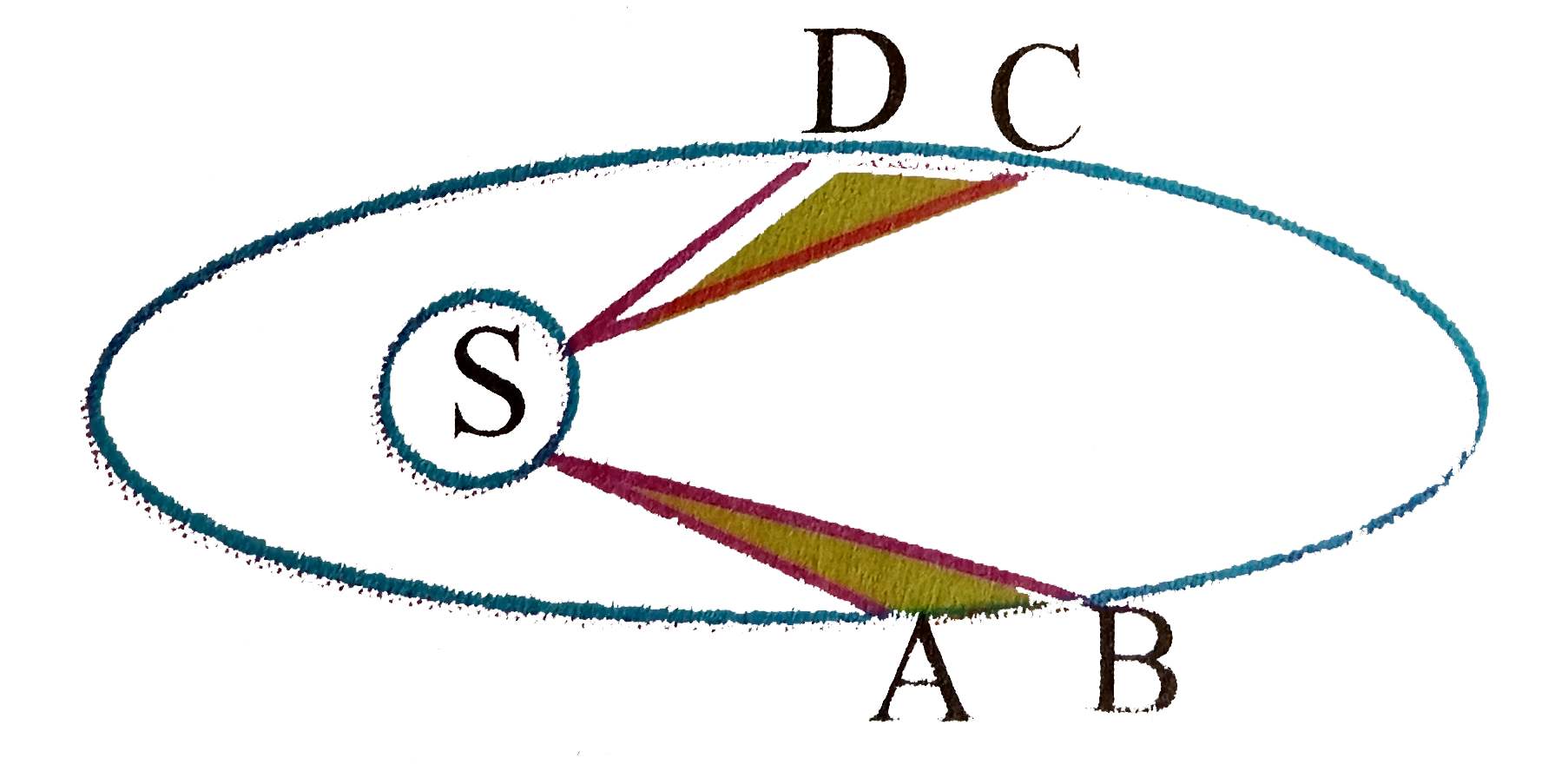B $- \frac{3 G M m}{8 a}$
C $- \frac{G M m}{5 a}$
Dnone of these
Question 3 - Select One
According the Kepler's law, the areal velocity of a planet around the sun, always
Aincreases
Bdecreases
Cremains constant
Dfirst increases and then decreases

NIKITA PUBLICATION-GRAVITATION-Multiple Choice Questions

Home
Ask Doubt
Profile