An A.C. source of voltage V=220 "sin" (100πt) volts is connected with R=50 Ohm.The time interval in which of the current goes from its peak value of half of the peak value is: (A) 1/400 sec (B) 1/50 sec (C) 1/300 sec (D) 1/200 sec
To solve the problem, we need to determine the time interval in which the current goes from its peak value to half of its peak value when connected to an AC source.
1. Identify the Voltage Equation:
The voltage of the AC source is given as:
V(t)=220sin(100πt) volts
2. Calculate Peak Current:
The peak current Imax can be calculated using Ohm's law:
Imax=VmaxR=22050=4.4 A
3. Write the Current Equation:
The current I(t) can be expressed as:
I(t)=Imaxsin(100πt)=4.4sin(100πt)
4. Find Time When Current is at Peak:
The current reaches its peak value when:
sin(100πt1)=1
This occurs at:
100πt1=π2⇒t1=1200 seconds
5. Find Time When Current is Half of Peak:
To find the time when the current is half of its peak value:
I(t2)=Imax2⇒4.4sin(100πt2)=2.2
Simplifying gives:
sin(100πt2)=12
This occurs at:
100πt2=π6⇒t2=1600 seconds
6. Calculate the Time Interval:
The time interval Δt from peak to half of peak is:
Δt=t2−t1=1600−1200
To perform this subtraction, we need a common denominator:
Δt=1600−3600=−2600=1300 seconds
Final Answer:
The time interval in which the current goes from its peak value to half of its peak value is:
Δt=1300 seconds
Thus, the correct option is (C) 1300 sec.
The voltage of the AC source is given as:
V(t)=220sin(100πt) volts
The peak current Imax can be calculated using Ohm's law:
Imax=VmaxR=22050=4.4 A
The current I(t) can be expressed as:
I(t)=Imaxsin(100πt)=4.4sin(100πt)
The current reaches its peak value when:
sin(100πt1)=1
This occurs at:
100πt1=π2⇒t1=1200 seconds
To find the time when the current is half of its peak value:
I(t2)=Imax2⇒4.4sin(100πt2)=2.2
Simplifying gives:
sin(100πt2)=12
This occurs at:
100πt2=π6⇒t2=1600 seconds
The time interval Δt from peak to half of peak is:
Δt=t2−t1=1600−1200
To perform this subtraction, we need a common denominator:
Δt=1600−3600=−2600=1300 seconds
The time interval in which the current goes from its peak value to half of its peak value is:
Δt=1300 seconds
Thus, the correct option is (C) 1300 sec.
Similar Questions
An alternating voltage v(t)=220sin100πt volt is applied to a pureluy resistive load of 50Ω. The time taken for the current to rise from half of the peak value to the peak value is :
View SolutionAn AC source is rated at 220V,50Hz. The time taken for voltage to change from its peak value to zero is
View SolutionA resistance of 20Ω is connected to a source of an alternating potential V=220sin(100πt). The time taken by the current to change from the peak value to rms value is
View SolutionA resistance of 20ohms is connected to a source of an alternating potential V=220sin(100πt). The time taken by the current to change from its peak value to r.m.s. value is
View SolutionA resistance of 20ohms is connected to a source of an alternating potential V=220sin(100πt). The time taken by the current to change from its peak value to r.m.s. value is
View SolutionThe current in an AC circuit is given byI=I0 sin (50 π)/t where t is in second. The time interval in which it will reach from zero to its peak value is
View SolutionIn an ac circuit , an alternating voltage e=200√2sin100t volts is connected to a capacitor of capacitance 1μF. The rms value of the current in the circuit is :
View SolutionIn an ac circuit an alternating voltage e=200√2sin100t volts is connected to a capacitor of capacity 1 μF. The rms.value of the current in the circuit is
View SolutionIn the figure shown, the reading of voltmeters are V1=40V,V2=40V and V3=10V. Find
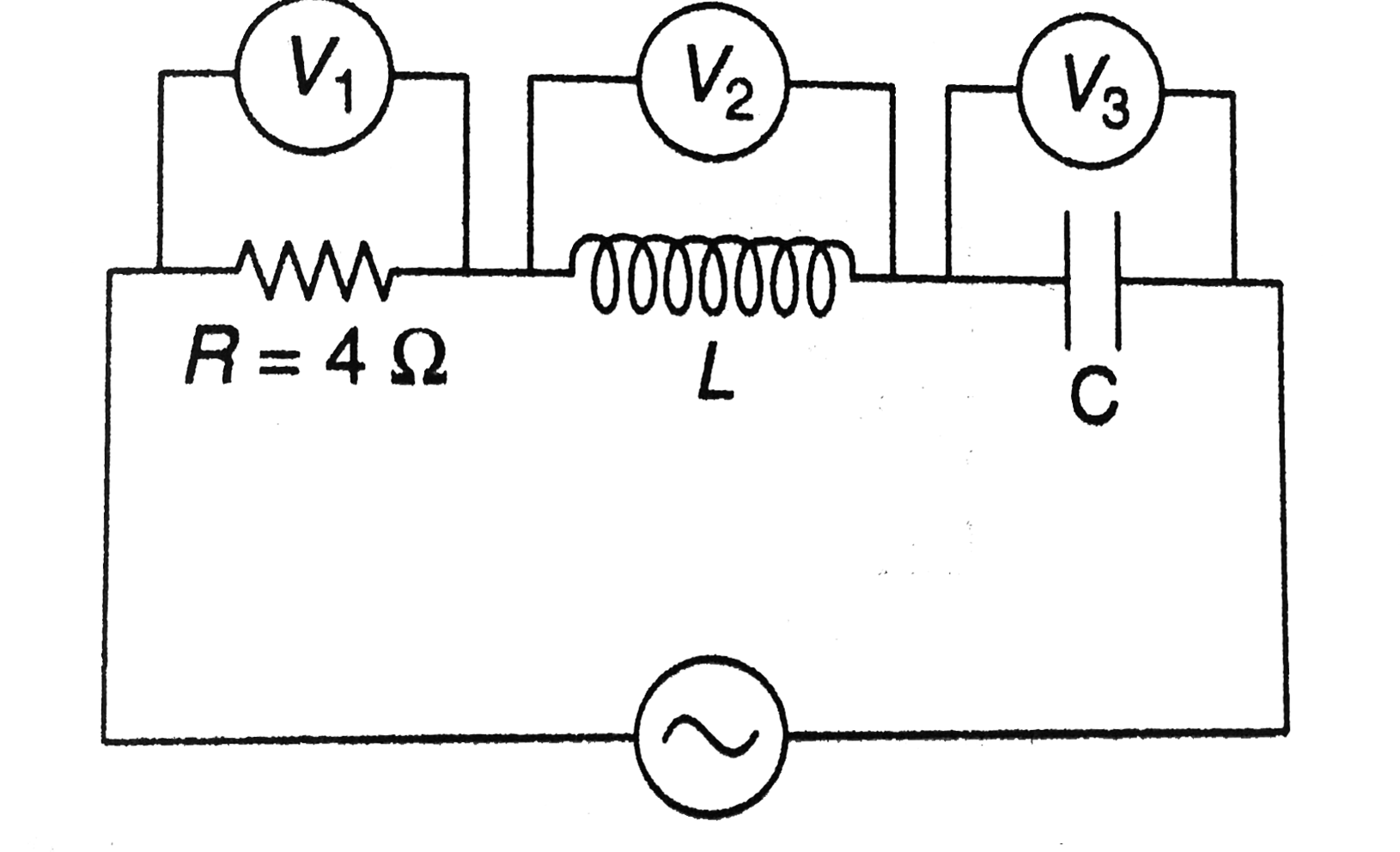
(a) the peak value of current
(b) the peak value of emf
(c) the value of L and C.
View SolutionWhat is the value of (tanθcosecθ)2−(sinθsecθ)2 (a) −1 (b) 0 (c) 1 (d) 2
View Solution
