An air core solenoid has 1000turns and is one metre long. Its cross-sectional area is 10cm2. Its self-inductance is
0.1256mH
12.56mH
1.256mH
125.6mH
The correct Answer is:C
To find the self-inductance L of the air core solenoid, we can use the formula for the self-inductance of a solenoid:
L=μ0N2Al
where:
- L = self-inductance (in henries)
- μ0 = permeability of free space =4π×10−7H/m
- N = number of turns (1000 turns)
- A = cross-sectional area (in square meters)
- l = length of the solenoid (1 meter)
Step 1: Convert the cross-sectional area from cm² to m²
The cross-sectional area A is given as 10cm2. We need to convert this to square meters:
A=10cm2=10×10−4m2=0.001m2
Step 2: Substitute the values into the self-inductance formula
Now we can substitute the values into the self-inductance formula:
L=μ0N2Al
Substituting the known values:
L=(4π×10−7)(1000)2(0.001)1
Step 3: Calculate L
Now we perform the calculations:
L=(4π×10−7)1000000×0.0011
L=(4π×10−7)×1000
L=4π×10−4H
Using π≈3.14:
L≈4×3.14×10−4≈1.256×10−3H
Step 4: Convert to millihenries
To convert henries to millihenries:
L≈1.256mH
Final Answer
The self-inductance of the air core solenoid is approximately:
L≈1.256mH
---
- L = self-inductance (in henries)
- μ0 = permeability of free space =4π×10−7H/m
- N = number of turns (1000 turns)
- A = cross-sectional area (in square meters)
- l = length of the solenoid (1 meter)
The cross-sectional area A is given as 10cm2. We need to convert this to square meters:
Now we can substitute the values into the self-inductance formula:
Now we perform the calculations:
L=(4π×10−7)×1000
L=4π×10−4H
To convert henries to millihenries:
The self-inductance of the air core solenoid is approximately:
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Inductor Circuits31videos
ELECTROMAGNETIC INDUCTION
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Applications Of Emi58videos
ELECTROMAGNETIC INDUCTION
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC INDUCTION
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test29videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM
Similar Questions
An air-cored solenoid has 150 turns and cross-sectional area 2cm2. If it is 40 cm long, what is its self-inductance?
View SolutionA straight solenoid of length 50 cm has 1000 turns per metre and mean cross-sectional area of 2×10−4m2 . It is placed with its axis of 30∘ with uniform magnetic field of 0.32 T . Find the torque acting on the solenoid when a current of 2 ampere is passed through it .
View Solution
Knowledge Check
- Question 1 - Select One
A long solenoid has 1000 turns and its area of cross -section is 10−4m2. If a magnetic induction of10−2T is produced in it on passing a current of 1A through it , then the magnetic flux linked with it will be
A10−1B10−2C10−3D10−4 - Question 2 - Select One
A circular coil with a cross-sectional area of 4cm2 has 10 turns. It is placed at the center of a long solenoid that has 15 turns/cm and a cross sectional area of 10cm2, shown in the figure. The axis of the coil conicides with the axis of the solenoid. What is their mutual inductance?
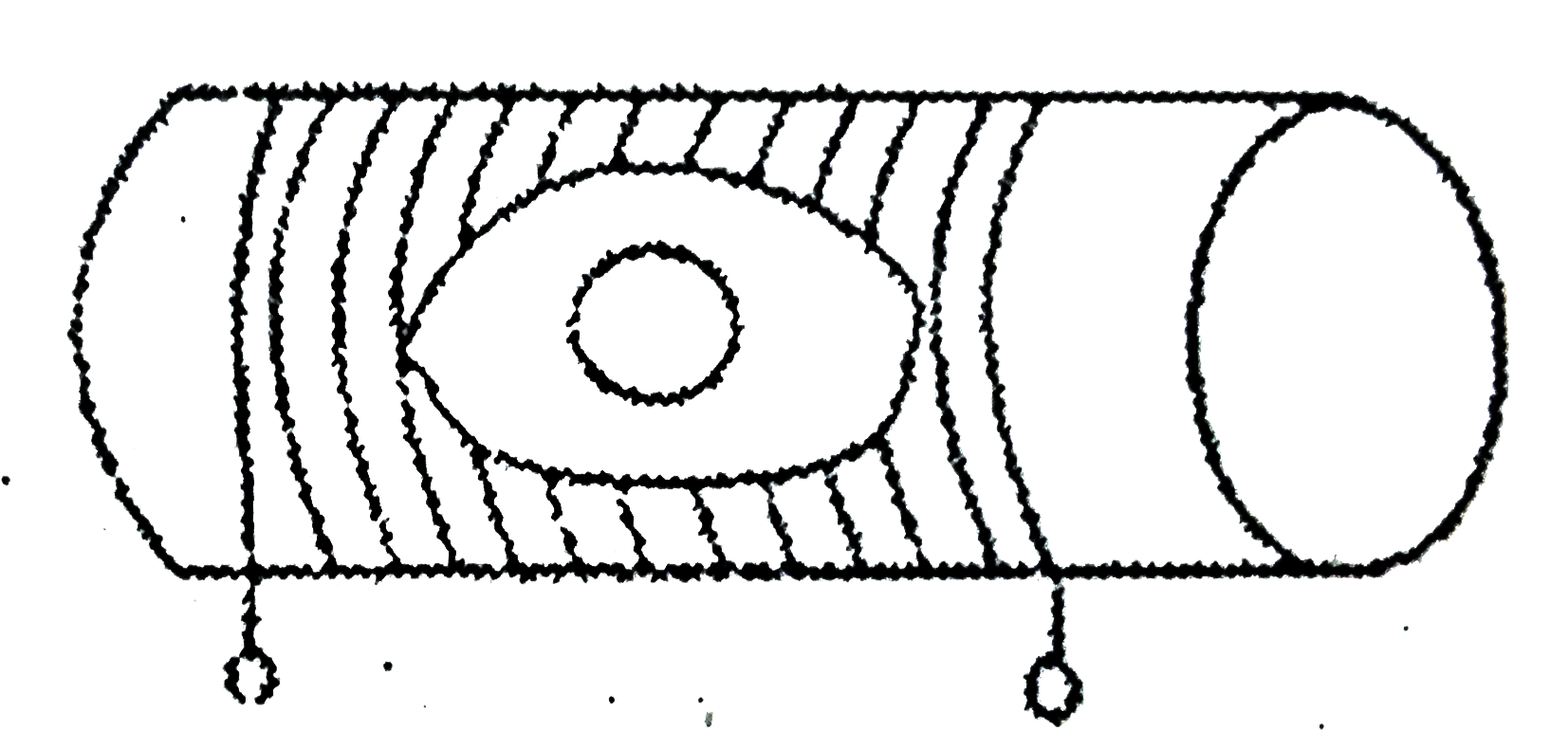 A7.54μHB8.54μHC9.54μHD10.54μH
A7.54μHB8.54μHC9.54μHD10.54μH
A straight solenoid of length 50cm has 1000 turns and a mean cross sectional area of 2×10−4m2. It is placed with its axis at 30∘ with a uniform magnetic field of 0⋅31T. Find the torque acting on the solenoid when a current of 2A is passed through it.
View SolutionA straight solenoid of length 50 cm has 1000 turns per metre and mean cross-sectional area of 2×10−4m2 . It is placed with its axis of 30∘ with uniform magnetic field of 0.32 T . Find the torque acting on the solenoid when a current of 2 ampere is passed through it .
View Solutiona. Calculate the inductance of an air core solenoid containing 300 turns if the length of the solenoid is 25.0cm and its cross -sectional area is 4.00cm2.
b. Calculate the self -induced emf in the solenoid if the current through it is decreasingg at the rate of 50.0A/s.View SolutionA toroid of 1000 turns has an average radius of 10 cm and area of cross section 15cm2. Calculate the self-inductance of the toroid.
View SolutionA solenoid of length 20cm, area of cross- section 4.0cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross - sectional area 8.0cm ^2 and length 10 cm. Find the mutual inductance between the solenoids.
View Solutiona. What is the magnetic flux through one turn of a solenoid of self inductance 8.0×10−5H when a current of 3.0A flows throgh it? Assume that the solemoid has 1000 turns ans is wound from wire of diameter 1.0mm.
b. What is the cross sectional area of the solenoid?View Solution

