An airplane with a speed of 97.5 m/s is climbing upward at an angle of 50.0∘ with respect to the horizontal. When the plane's altitude is 732 m, the pilot releases a package, (a) Calculate the distance along the ground, measured from a point directly beneath the point of release, to where the package hits the earth.
+425m
+1380m
−678m
−2880m
The correct Answer is:B
To solve the problem of the package released from the airplane, we will follow these steps:
Step 1: Determine the initial velocity components of the package.
The airplane is moving at a speed of 97.5 m/s at an angle of 50 degrees with respect to the horizontal. We need to find the horizontal and vertical components of this velocity.
- Horizontal component (Vx):
Vx=V⋅cos(θ)=97.5⋅cos(50∘)
- Vertical component (Vy):
Vy=V⋅sin(θ)=97.5⋅sin(50∘)
Step 2: Calculate the vertical motion of the package.
The package is released from an altitude of 732 m. We will use the second equation of motion to find the time it takes for the package to hit the ground.
The equation is:
h=Vy⋅t+12a⋅t2
Where:
- h=−732 m (the negative sign indicates a downward displacement),
- Vy is the initial vertical velocity calculated in Step 1,
- a=−9.8m/s2 (acceleration due to gravity).
Step 3: Rearrange the equation into standard quadratic form.
Rearranging gives us:
12at2+Vyt+h=0
Substituting the values, we get:
4.9t2−Vyt−732=0
Step 4: Solve the quadratic equation for time (t).
Using the quadratic formula:
t=−b±√b2−4ac2a
Where:
- a=4.9,
- b=−Vy,
- c=−732.
Step 5: Calculate the horizontal distance traveled.
Once we have the time t from Step 4, we can calculate the horizontal distance d traveled by the package using:
d=Vx⋅t
Step 6: Final calculation and conclusion.
Substituting the values will give us the distance along the ground from the point directly beneath the release point to where the package hits the earth.
---
The airplane is moving at a speed of 97.5 m/s at an angle of 50 degrees with respect to the horizontal. We need to find the horizontal and vertical components of this velocity.
Vx=V⋅cos(θ)=97.5⋅cos(50∘)
- Vertical component (Vy):
Vy=V⋅sin(θ)=97.5⋅sin(50∘)
The package is released from an altitude of 732 m. We will use the second equation of motion to find the time it takes for the package to hit the ground.
h=Vy⋅t+12a⋅t2
Where:
- h=−732 m (the negative sign indicates a downward displacement),
- Vy is the initial vertical velocity calculated in Step 1,
- a=−9.8m/s2 (acceleration due to gravity).
Rearranging gives us:
12at2+Vyt+h=0
Substituting the values, we get:
4.9t2−Vyt−732=0
Using the quadratic formula:
t=−b±√b2−4ac2a
Where:
- a=4.9,
- b=−Vy,
- c=−732.
Once we have the time t from Step 4, we can calculate the horizontal distance d traveled by the package using:
d=Vx⋅t
Substituting the values will give us the distance along the ground from the point directly beneath the release point to where the package hits the earth.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)14videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
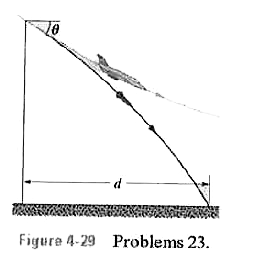
A certain airplane has a speed of 290.0 km/h and is diving at an angle of θ=30.0∘ below the horizontal when the pilot releases a radar decoy. The horizontal distance between the release point and the point where the decoy strikes the ground is d = 700 m. (a) How long is the decoy in the air? (b) How high was the release point?
 View Solution
View SolutionA ball is thrown from a field with a speed of 12.0 m/s at an angle of 450 with the horizontal. At what distance will it hit the field again ? Take g=10.0ms2
View Solution
Knowledge Check
- Question 1 - Select One
A shot putter with a mass of 80 kg pushes the iron ball of mass of 6 kg from a standing position accelerating it uniformly from rest at an angle of 45∘ with the horizontal during a time interval of 0.1 seconds. The ball leaves his hand when it is 2m high above the level, ground and hits the ground 2 seconds later.
The horizontal distance between the point of release and the point where the ball hits the ground :A16 mB18 mC20 mD22 m - Question 2 - Select One
A shot putter with a mass of 80kg pushes the iron ball of mass of 6kg from a standing position accelerating it uniformly form rest at an angle of 45∘ with the horizontal during a time interval of 0.1 seconds. The ball leaves his hand when it 2m high above the level ground and hits the ground 2 seconds later (g=10m/s2).
The horizontal disatnce between the point of release and the point where the ball hits the ground .A16mB18mC20mD22m - Question 3 - Select One
A fighter plane moving with a speed of 50√2ms−1 upward at an angle of 45∘ with the vertical releases a bomb when it was at a height 1000m from ground. Find
(a) the time of flight
(b) the maximum height of the bomb above ground.A10s , 1000mB20s , 125mC20s , 1125mDNone
A projectile of mass "m" is projected from ground1 with a speed of 50 m/s at an angle of 53∘ with the horizontal. It breaks up into two equal parts at the highest point of the trajectory. One particle coming to rest immediately after the explosion.
The distance between the pieces of the projectile when they reach the ground are :View SolutionA ball is projected from a point on the floor wilth a speed of 15 m/s at an angle of 600 with the horizontal. Will ilt hit a vertical wall 5 m away from the point of projection and perpendiculaer to the plane of projection without and perpendicular to the plane of projection without hitting the floor? will the answer differ if the wall is 22 m away?
View SolutionA stone is thrown from the top of a tower of height 50 m with a velocity of 30 m per second at an angle of 30∘ above the horizontal. Find (a) the time during which the stone will be in air, (b) the distance from the tower base to where the stone will hit the ground, (c) the speed with which the stone will hit the ground, (d) the angle formed by the trajectory of the stone with the horizontal at the point of hit.
View SolutionAn airplane, diving at an angle of 53.0∘ with the vertical releases a projectile at an altitude of 730 m. The projectile hits the ground 5.00 s after being released. What is the speed of the aircraft?
View SolutionAn airplane, diving at an angle of 53.0∘ with the vertical releases a projectile at an altitude of 730 m. The projectile hits the ground 5.00 s after being released. What is the speed of the aircraft?
View Solution

