An amount n (in moles) of a monatomic gas at initial temperature T0 is enclosed in a cylinderical vessel fitted with a ligth piston. The surrounding air has a temperature Ts(>T0) . And the atmospheric pressure is Pa . Heat may be conducted between the surrounding and the gas through the bottom of the cylinder. The bottom has a surface area A, thickness x and thermal conductivity K. Assuming all change to be slow, find the distance moved by the piston in time t.
The correct Answer is:A, B
(Qt)=KA(T8−T0)X
=nCpdTX=KA(T8−T0)X
⇒n5/2RdTdt=KA(T8−T0)X
+>5nR2dTdt=KA(T8−T0)X
dTT8−T0=−2KAdt5nRX
(T8−T0)TT0
−2KAdt5nRX
⇒InT8−TT8−T0)=−2KAdt5nRX
⇒T8−T=(T−8−T0)e−2KAt/(5nRX)
T=(T8−T0)e−2KAt5nRX
⇒PaAlnR=T−T0
(T_8-T_0)(T_8-T_0)e^(-2KAt)/(5nRX)<br>(T_8-T_0)((1-e^(-2KAt)/(5nRX))<br>=(nR)/(P_aA)xx(T_8-T_0)((1-e^(-2KAt)/(5nRX)).
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE
1 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - Objective 2
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
Similar Questions
A monoatomic ideal gas, initially at temperature T1 is enclosed in a cylinder fitted with a frictionless piston. The gas is allowed to expand adiabatically to a temperature T2 by releasing the piston suddenly. If L1 and L2 are the lengths of the gas column. before and after expansion respectively, then T1T2 is given by
View SolutionOne mole of a perfect gas in a cylinder fitted with a piston has a pressure P, volume V and temperature T. if the temperature is increased by 1K keeping pressure constant, the increase in volume is
View Solution
Knowledge Check
The air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P0 and T0. The atmospheric pressure is also P0. At a later time, tension in the string is 38P0A where A is cthe cross-sectional are of the cylinder. at this time, the temperature of the gas has become.
 A38T0B34T0C118T0D138T0
A38T0B34T0C118T0D138T0A monatomic ideal gas, initially at temperature T1, is enclosed in a cylinder fitted with a frictionless piston. The gas is allowed to expand adiabatically to a temperature T2 by releasing the piston suddenly. If L1andL2 are the length of the gas column before expansion respectively, then T1T2 is given by
A(L1L2)2/3B(L1L2)C(L2L1)D(L2L1)2/3One mole of an ideal monatomic gas at temperature T0 expands slowly according to the law PV = constant. If the final temperature is 2T0, heat supplied to the gas is
A2RT0BRT0C32RT0D12RT0
A vessel contains 1 mole of 0, gas (molar mass =32 ) at a temperature T. The pressure of the gas is P. An identical vessel containing one mole of He gas (molar mass = 4) at a temperature 2T, has a pressure of nP. Find u.
View SolutionOne mole of an ideal monatomic gas has initial temperature T0, is made to go through the cycle abca shown in Fig. If U denotes the internal energy, then choose the correct alternative
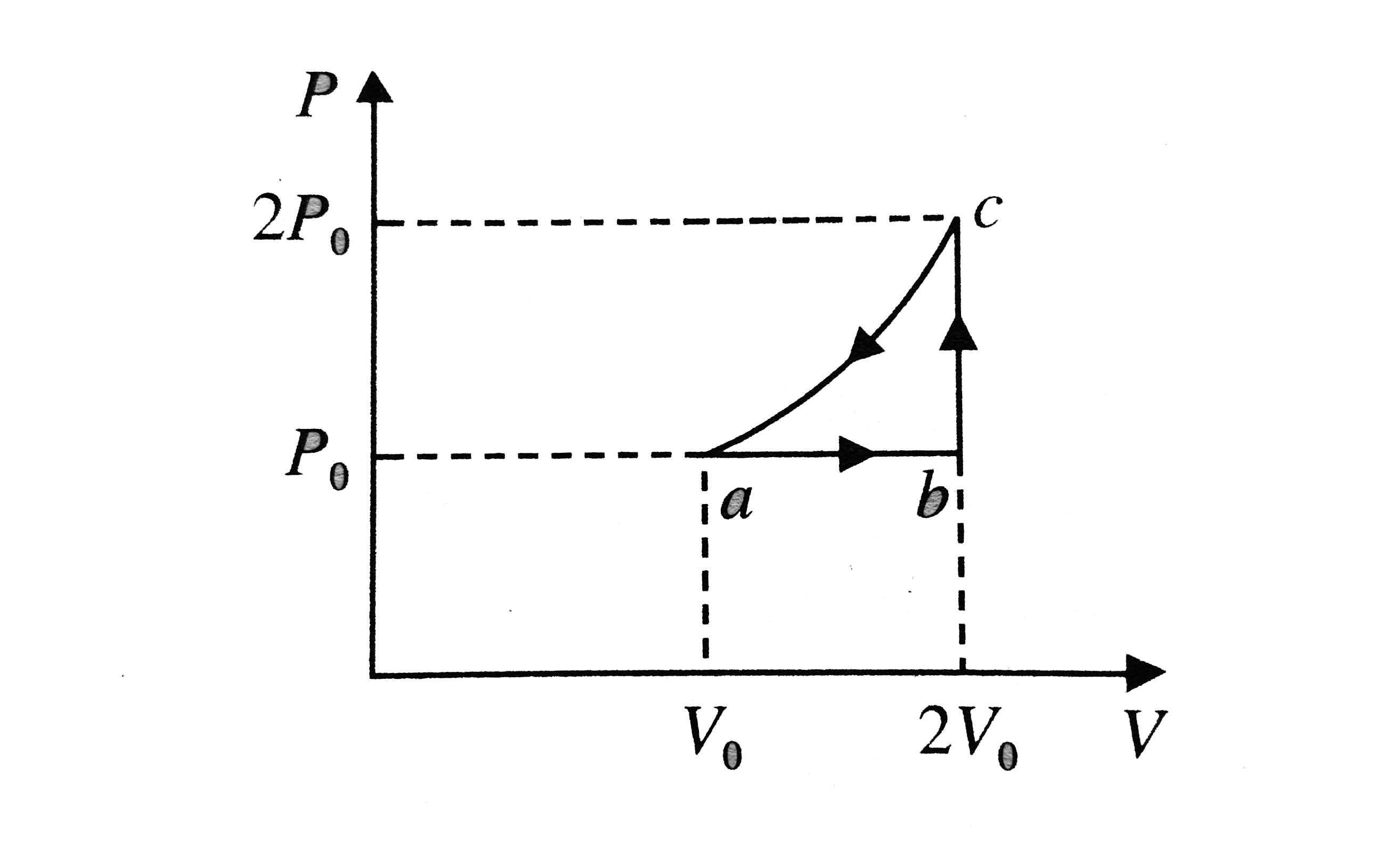
View SolutionOne mole of monatomic gas is brought from state A to state B. The initial temperature at A is T0. The temperature at B will be –

View SolutionA vessel contains 1 mole of O2 at a temperature T. The pressure of gas is P. An identical vessel containing 1 mole of the gas at a temperature 2T has pressure of -
View SolutionOne mole of an ideal monatomic gas at temperature T0 expands slowly according to the law P=kV (k is constant). If the final temperature is 4T0 then heat supplied to gas is
View Solution
