An arc of radius r carries charge. The linear density of charge is λ and the arc subtends an angle π3 at the centre.
λ4ε0
λ8ε0
λ12ε0
λ16ε0
The correct Answer is:C
To solve the problem, we need to calculate the electric potential V at the center of an arc of radius r that carries a linear charge density λ and subtends an angle of π3 at the center.
1. Identify the Given Values:
- Radius of the arc, r
- Linear charge density, λ
- Angle subtended at the center, θ=π3
2. Calculate the Length of the Arc:
The length L of the arc can be calculated using the formula:
L=rθ
Substituting the value of θ:
L=r⋅π3=rπ3
3. Calculate the Total Charge Q on the Arc:
The total charge Q on the arc can be found using the linear charge density:
Q=λ⋅L
Substituting the expression for L:
Q=λ⋅rπ3=λrπ3
4. Use the Formula for Electric Potential V:
The electric potential V at a distance r from a point charge is given by:
V=kQr
where k=14πϵ0.
5. Substitute Q into the Potential Formula:
Substituting the expression for Q:
V=kλrπ3r
The r in the numerator and denominator cancels out:
V=kλπ3
6. Substitute the Value of k:
Now substitute k=14πϵ0:
V=14πϵ0⋅λπ3
7. Simplify the Expression:
Simplifying the expression gives:
V=λ12ϵ0
8. Final Result:
Therefore, the electric potential V at the center of the arc is:
V=λ12ϵ0
Conclusion:
The correct option is λ12ϵ0.
- Radius of the arc, r
- Linear charge density, λ
- Angle subtended at the center, θ=π3
The length L of the arc can be calculated using the formula:
L=rθ
Substituting the value of θ:
L=r⋅π3=rπ3
The total charge Q on the arc can be found using the linear charge density:
Q=λ⋅L
Substituting the expression for L:
Q=λ⋅rπ3=λrπ3
The electric potential V at a distance r from a point charge is given by:
V=kQr
where k=14πϵ0.
Substituting the expression for Q:
V=kλrπ3r
The r in the numerator and denominator cancels out:
V=kλπ3
Now substitute k=14πϵ0:
V=14πϵ0⋅λπ3
Simplifying the expression gives:
V=λ12ϵ0
Therefore, the electric potential V at the center of the arc is:
V=λ12ϵ0
The correct option is λ12ϵ0.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.4
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Knowledge Check
Calculate the length of the arc of a circle of radius 31.0 cm which subtands and angle of π6 at the centre.
A11.7 cmB14.7 cmC16.7 cmD15.7 cm
Find the length of an arc of circle of radius 6cm subtending an angle of 15∘ at the centre.
View SolutionA uniform circular loop of radius a and resistance R is pulled at a constant velocity v out of a region of a uniform plane of the loop and the velocity are both perpendicular to B. Then the electrical power in the circular loop at the instant when the arc (of the circular loop) outside the region of magnetic field subtends an angle π3 at the centre of the loop is
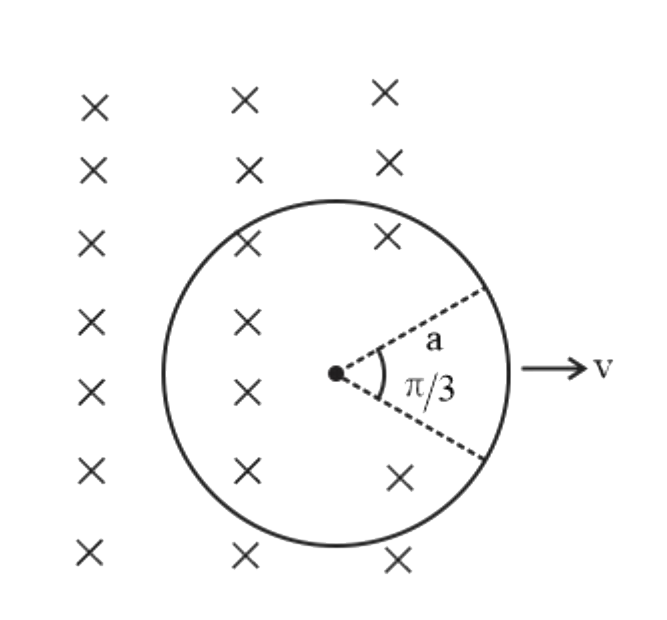
View SolutionFind the length of an arc of a circle of radius 10cm subtending an angle of 300 at the centre
View SolutionA ring of radius R carries a non - uniform charge of linear density λ=λ0cosθ sec in the figure) Magnitude of the net dipolement of the ring is :

View SolutionThe radius of the circle whose arc of length 15 π cm makes an angle of 3π4 radians at the centre is
View SolutionA wire carrying current I is tied between points P and Q and is in the shape of a circular arc of radius R due to a uniform magnetic field B (perpendicular to the plane of the paper, shown by xxx) in the vicinity of the wire. If the wire subtends an angle 2θ0 at the centre of the circle (of which it forms an arc) then the tension in the wire is:

View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View Solution
