An athlete runs along a circular track with a constant speed of 5 m/s . If A,B and C are his instantaneous positions at different times then find the change in velocity (a) from A to B and (b) from A to C.
To solve the problem, we need to determine the change in velocity of the athlete as he moves from point A to point B and from point A to point C on a circular track, given that he runs with a constant speed of 5 m/s.
1. Identify the Velocity Vectors at Points A, B, and C:
- Since the athlete is running with a constant speed of 5 m/s along a circular track, we can represent the velocity vectors at points A, B, and C.
- Let's assume:
- At point A, the velocity vector vA=5^i (moving in the positive x-direction).
- At point B, the velocity vector vB=−5^j (moving in the negative y-direction).
- At point C, the velocity vector vC=−5^i (moving in the negative x-direction).
2. Calculate the Change in Velocity from A to B:
- The change in velocity ΔvAB from A to B is given by:
ΔvAB=vB−vA
- Substituting the values:
ΔvAB=(−5^j)−(5^i)=−5^i−5^j
3. Calculate the Magnitude of the Change in Velocity from A to B:
- The magnitude of ΔvAB is calculated using the Pythagorean theorem:
|ΔvAB|=√(−5)2+(−5)2=√25+25=√50=5√2 m/s
4. Determine the Direction of the Change in Velocity from A to B:
- The angle θ made with the negative x-axis can be found using:
tanθ=55=1⟹θ=45∘
- Thus, the change in velocity from A to B has a magnitude of 5√2 m/s and is directed at an angle of 45∘ from the negative x-axis.
5. Calculate the Change in Velocity from A to C:
- The change in velocity ΔvAC from A to C is given by:
ΔvAC=vC−vA
- Substituting the values:
ΔvAC=(−5^i)−(5^i)=−10^i
6. Calculate the Magnitude of the Change in Velocity from A to C:
- The magnitude of ΔvAC is:
|ΔvAC|=|−10|=10 m/s
7. Determine the Direction of the Change in Velocity from A to C:
- The direction is simply towards the negative x-axis (left).
Final Answers:
- (a) Change in velocity from A to B:
- Magnitude: 5√2 m/s, Direction: 45∘ from the negative x-axis.
- (b) Change in velocity from A to C:
- Magnitude: 10 m/s, Direction: Negative x-axis.
- Since the athlete is running with a constant speed of 5 m/s along a circular track, we can represent the velocity vectors at points A, B, and C.
- Let's assume:
- At point A, the velocity vector vA=5^i (moving in the positive x-direction).
- At point B, the velocity vector vB=−5^j (moving in the negative y-direction).
- At point C, the velocity vector vC=−5^i (moving in the negative x-direction).
- The change in velocity ΔvAB from A to B is given by:
ΔvAB=vB−vA
- Substituting the values:
ΔvAB=(−5^j)−(5^i)=−5^i−5^j
- The magnitude of ΔvAB is calculated using the Pythagorean theorem:
|ΔvAB|=√(−5)2+(−5)2=√25+25=√50=5√2 m/s
- The angle θ made with the negative x-axis can be found using:
tanθ=55=1⟹θ=45∘
- Thus, the change in velocity from A to B has a magnitude of 5√2 m/s and is directed at an angle of 45∘ from the negative x-axis.
- The change in velocity ΔvAC from A to C is given by:
ΔvAC=vC−vA
- Substituting the values:
ΔvAC=(−5^i)−(5^i)=−10^i
- The magnitude of ΔvAC is:
|ΔvAC|=|−10|=10 m/s
- The direction is simply towards the negative x-axis (left).
- (a) Change in velocity from A to B:
- Magnitude: 5√2 m/s, Direction: 45∘ from the negative x-axis.
- (b) Change in velocity from A to C:
- Magnitude: 10 m/s, Direction: Negative x-axis.
Topper's Solved these Questions
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - ADDITIONAL SOLVED PROBLEMS
22 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - EXAMPLES
26 Videos
- UNITSBOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (SELECTED PROBLEMS)
38 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - From Musical Sound
10 Videos
Similar Questions
A car is moving round a circular track with a constant speed vof20ms−1 (As shown in figure).At different times,the car is at A,B and C,respectively . Find the velocity change (a) from A to C, and (b) from A to B.
 .
.
View SolutionAn athlete runs along a circular track of circumference 400 m with a uniform speed 15 m/s . What is the change in velocity when the runs through a distance (i) 100 m (ii) 200 m ?
View Solution
Knowledge Check
A particle is moving on a circular path with a constant speed v. Its change of velocity as it moves from A to B is:
 A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A particle of mass 2 kg moves on a circular path with constant speed 10 m/ s . Find change in speed and magnitude of change in velocity. Whan particle completes half revolution.
View SolutionA particle of mass 2 kg is moving in circular path with constant speed 20 m/s. The magnitude of change in velocity when particle travels from A to P will be
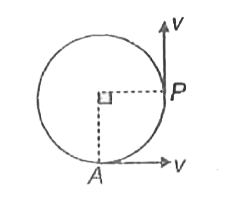
View SolutionConsider
 .
.
The potential difference VA−VB is.
View SolutionIf a girl runs around a circular track of length 400 m and comes back to the initial point in 40 s, what would be her speed and velocity?
View SolutionJoseph jogs from one end A to other end B of a straight 300m road in 2 minutes 30 seconds and then turns around and jogs 100m back to point C in another 1 minute. What are Joseph's average speeds and velocities in Jogging (a) from A to B and (b) from A to C?
View SolutionA girl runs along a circular track of radius 5 m starting from point A. What will be the distance travelled by her and speed
if she stops halfway at B in 400 s?
View SolutionA girl runs along a circular track of radius 5 m starting from point A. What will be the distance travelled by her and speed
if she comes back to the initial position in 300 s
View Solution
