An elastic string of length 42cm and cross section area 10−4m2 is attached between two pegs at distance 6mm as shown in the figure. A particle of mass m is kept at midpoint of string stretched as shown in figure by 20cm and released. As th string attains natural length, the particle attains a speed of 20m/s. Then young modulus Y of string is of order (A) 10∘ (B) 1012 (C) 108 (D) 104
To solve the problem, we need to find the Young's modulus (Y) of the elastic string using the information provided. We will apply the principle of conservation of energy.
1. Understanding the Problem:
- The elastic string has an original length L=42cm=0.42m.
- It is stretched by ΔL=20cm=0.2m.
- The cross-sectional area A=10−4m2.
- The particle attains a speed v=20m/s when the string returns to its natural length.
2. Using Conservation of Energy:
- The potential energy stored in the stretched string is converted into kinetic energy of the mass when the string returns to its natural length.
- The potential energy U stored in the string can be expressed as:
U=12YΔLL2V
where V is the volume of the string, given by V=A⋅L.
3. Calculate the Volume:
- The volume V of the string is:
V=A⋅L=(10−4m2)⋅(0.42m)=4.2×10−5m3
4. Kinetic Energy of the Mass:
- The kinetic energy K of the mass when it reaches the speed v is:
K=12mv2
5. Equating Potential Energy to Kinetic Energy:
- Setting the potential energy equal to the kinetic energy:
12YΔLL2(A⋅L)=12mv2
- Simplifying, we get:
YΔL2LA=mv2
6. Rearranging for Young's Modulus:
- Rearranging the equation to solve for Young's modulus Y:
Y=mv2LAΔL2
7. Substituting Known Values:
- Now we need to substitute the known values. However, we do not have the mass m directly. We will express Y in terms of m:
Y=m(20)2(0.42)(10−4)(0.2)2
- Simplifying further:
Y=m⋅400⋅0.4210−4⋅0.04
Y=m⋅1684×10−6=4.2×107m
8. Finding the Order of Young's Modulus:
- Since m is not given, we can assume it to be a small mass (let's say m is on the order of 1kg for estimation).
- Thus, Y is approximately 4.2×107N/m2, which is of the order 107.
Conclusion:
The order of Young's modulus Y of the string is approximately 107N/m2.
- The elastic string has an original length L=42cm=0.42m.
- It is stretched by ΔL=20cm=0.2m.
- The cross-sectional area A=10−4m2.
- The particle attains a speed v=20m/s when the string returns to its natural length.
- The potential energy stored in the stretched string is converted into kinetic energy of the mass when the string returns to its natural length.
- The potential energy U stored in the string can be expressed as:
U=12YΔLL2V
where V is the volume of the string, given by V=A⋅L.
- The volume V of the string is:
V=A⋅L=(10−4m2)⋅(0.42m)=4.2×10−5m3
- The kinetic energy K of the mass when it reaches the speed v is:
K=12mv2
- Setting the potential energy equal to the kinetic energy:
12YΔLL2(A⋅L)=12mv2
- Simplifying, we get:
YΔL2LA=mv2
- Rearranging the equation to solve for Young's modulus Y:
Y=mv2LAΔL2
- Now we need to substitute the known values. However, we do not have the mass m directly. We will express Y in terms of m:
Y=m(20)2(0.42)(10−4)(0.2)2
- Simplifying further:
Y=m⋅400⋅0.4210−4⋅0.04
Y=m⋅1684×10−6=4.2×107m
- Since m is not given, we can assume it to be a small mass (let's say m is on the order of 1kg for estimation).
- Thus, Y is approximately 4.2×107N/m2, which is of the order 107.
The order of Young's modulus Y of the string is approximately 107N/m2.
Similar Questions
A blocked of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.

View SolutionA block of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.

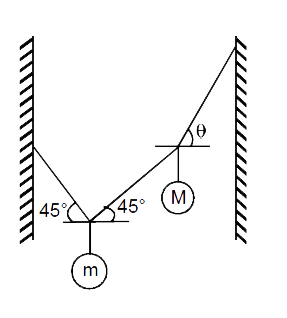
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
View SolutionA particle of mass m is doing horizontal circular motion with the help of a string (conical pendulum) as shown in the figure. If speed of the particle is constant then,
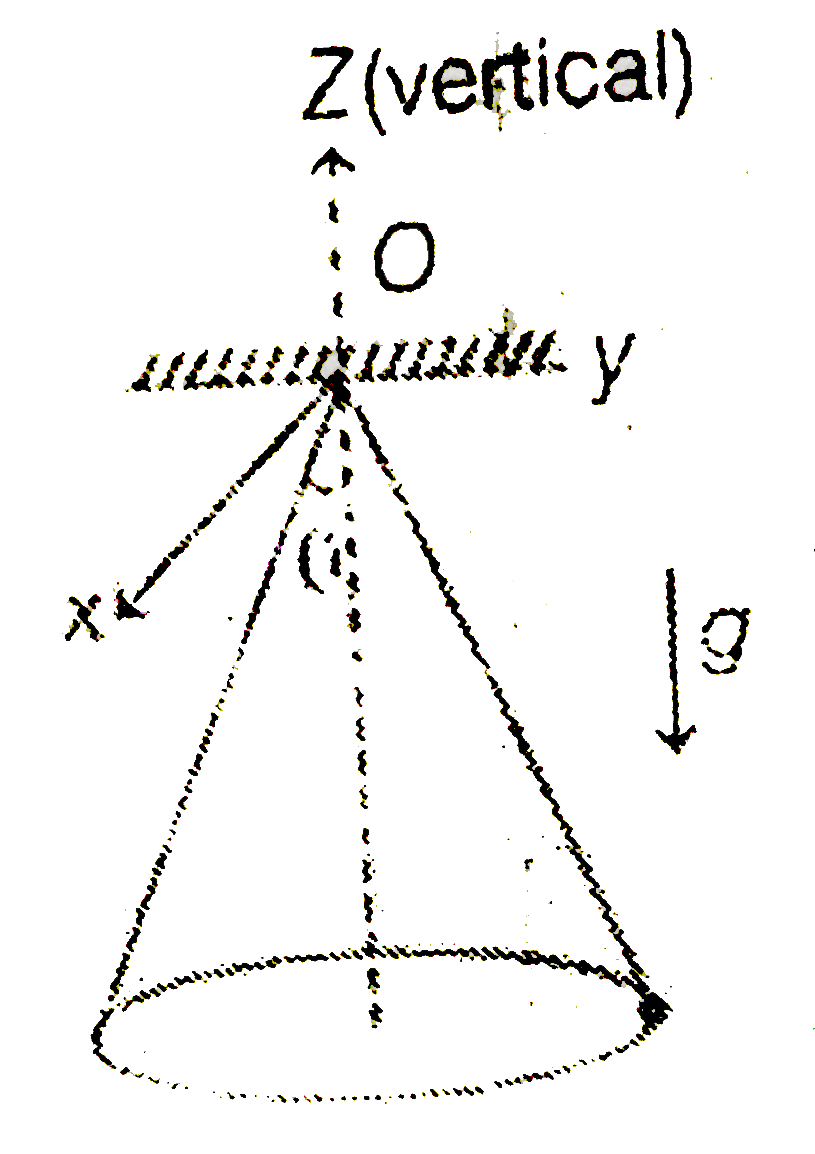
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA string of length and mass per unit length is used in atwood machine as shown in the figure. Masses of blocks are large in comparison with the mass of string. The transverse wave velocity in the string is:
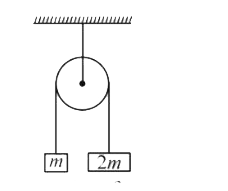
View SolutionA string of length and mass per unit length is used in atwood machine as shown in the figure. Masses of blocks are large in comparison with the mass of string. The transverse wave velocity in the string is:

View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
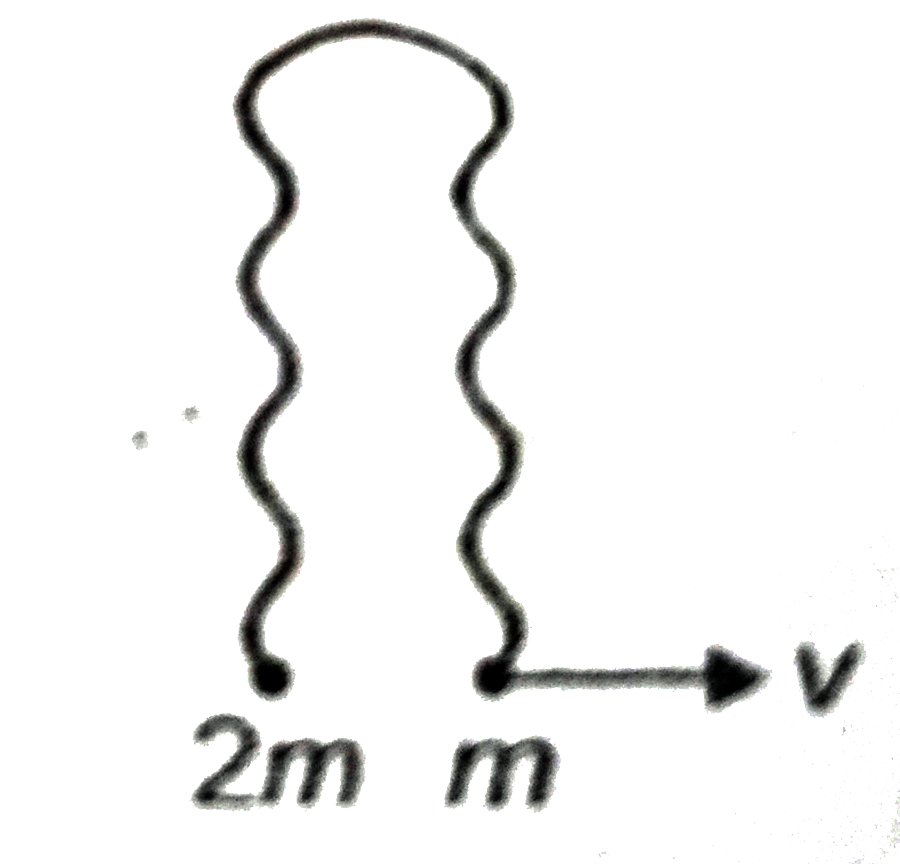
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.

View SolutionA uniform string of length 10m and mass 20 kg lies on a smooth frictionless inclined plane. A force of 200N is applied as shown in the figure.

(a) Find the acceleration of the string.
(b) Find the tension in the string at 2m from end A.
View Solution
