An electric dipole formed by two particles fixed at the ends of a light rod of length l. The mass of each particle is m and the charges are -q and +q . The system is placed in such a way that the dipole axis is parallel to a uniform electric field E that exist in the region. The dipole is slightly rotated abut its centre and released. Show that for small angular displacement, the motion is angular simple harmonic and find its time period.
 Solution in Tamil
Solution in Tamil
Suppose, the dipole axis makes an angle θ with
the electric field at an instant. The magnitude of the
torque on it is
|τ|=∣∣→p×→E∣∣
=qlEsinθ.
This torque will tend to rotate the dipole back towards
the electric field. Also, for small angular displacement
sinθ=≈θsotˆ
τ=−qlEθ.
The moment of inertia of the system about the axis of
rotation is
I=2×m(l2)2=ml22.
Thus the angular acceleration is
α=τI=−2qEmlθ=−ω2θ
. where ω2=2qEml
Thus, the motion is angular simple harmonic and the
time period is T=2π√ml2qE.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercise
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
98 Videos
Similar Questions
The charge on a proton is +1.6X10(−19)C and that on an
. electron is −1.6X10(−19)C. Does it mean that the electron
. has a charge 3.2X10(−19)c less than the charge of a
. proton?
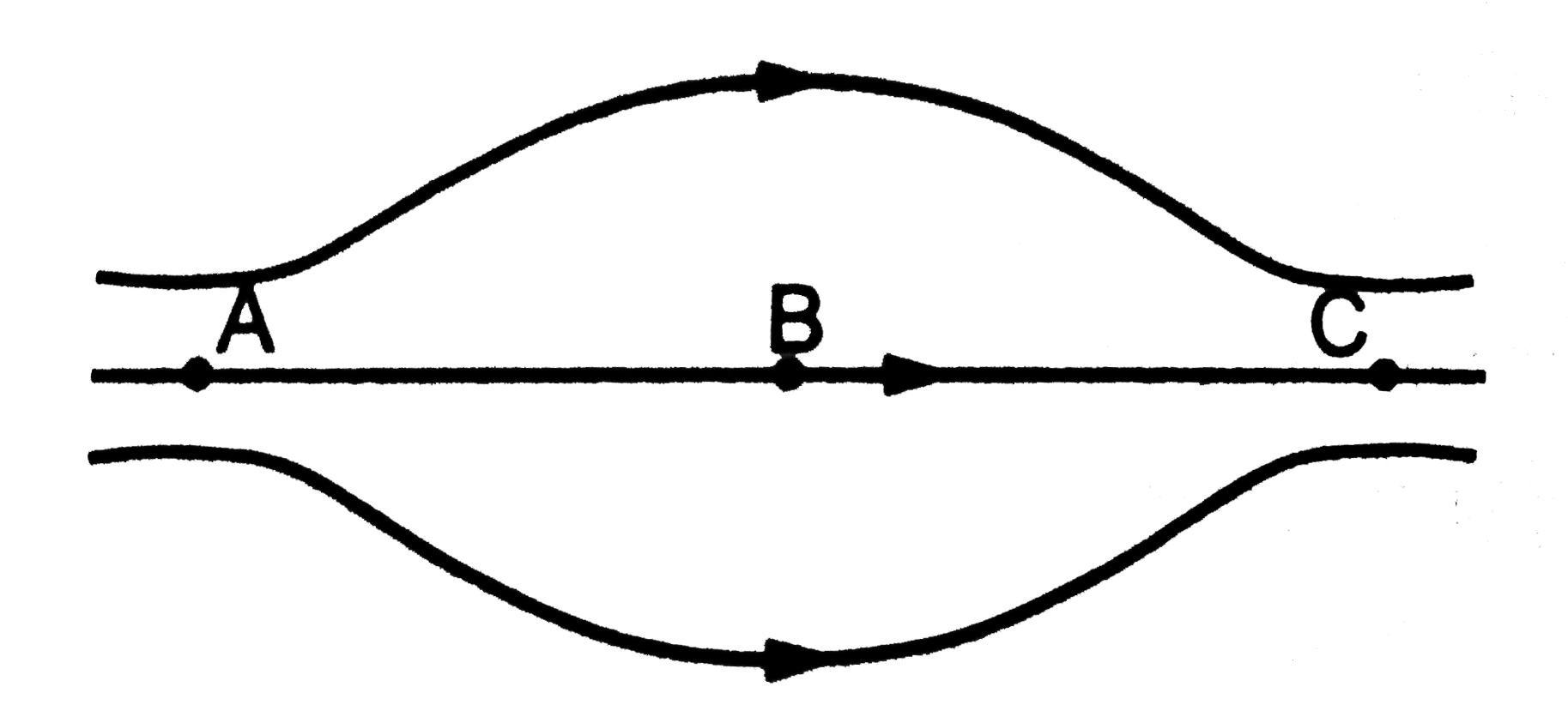
View SolutionFigure shows some of the electric field lines correspoinding to an electric field. The figure suggests that
View SolutionFind the dimensional formula of ε0 .
View SolutionA discharge tube contains helium at a low pressure. A large potential difference is applied across the tube. Consider a helium atom that has just been ionized due to the detachment of an atomic electron. Find the ratio of the distance travelled by the free electron to that by the positive ion in a short time dt after the ionization.
View SolutionCalculate the dimensions of (a) ∫→E.d→l,(b)vBlanddΦ0dt. The symbols have their usual meanings.
View SolutionTwo particles, carrying charges -q and +q and having equal masses m each, are fixed at the rod is clamped at an end and is placed in a uniform electric field E with the axis of the dipole along the electric field. The rod is slightly tlted and then released. Neglecting gravity find the time period of small oscillations.
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field, the force on it and its potential energy are respectively
View SolutionAn electric dipole is formed two particles fixed at the ends of a light rad of length I . The mass of each particle is m and charges are -q and +q The system is suspended by a torsionless thread in an electric field of intensity E that the dipole axis is parallel to the field if it is slightly displaced the period of angular motion is
View SolutionAn electric dipole (AB) consisting of two particles of equal and opposite charge and same mass is released in an electric field. In the figure field lines are without considering effect of field of dipole. The centre of mass of the dipole
View SolutionAn electric dipole (AB) consisting of two particles of equal and opposite charge and same mass is released in an electric field. In the figure field lines are without considering effect of field of dipole.

Angular acceleration of the dipole, immediately after it is released
View SolutionA charge q is placed at (1,2,1) and another charge -q is placed at (0,1,0) such that they form an electric dipole . There exists a uniform electric field vecE =(2hati +3hatj). the torque experienced by the dipole is -
View SolutionAn electric dipole had been formed by placing two particles each of mass m at the two ends of a light rod of length l. The charges of the two particles are +q and -q . This dipole is placed in a uniform electric field E in such a way that its axis is parallel to the direction of the field. The dipole is now deflected through a small angle. Show that for small angular displacement, the dipole will execute angular simple harmonic motion. Calculate the time period of the simple harmonic motion.
View SolutionAn electric dipole of dipole moment p is aligned parallel to a uniform electric field E. the energy required to rotate the dipole by 90^(@) is
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. It its dipole moment is along the direction of the field, the force on it and its potential energy are, respectively.
View SolutionA dipole is placed in a uniform electric field with its axis parallel to the field. It experiences
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field, the force on it and its potential energy are respectively
View Solution
