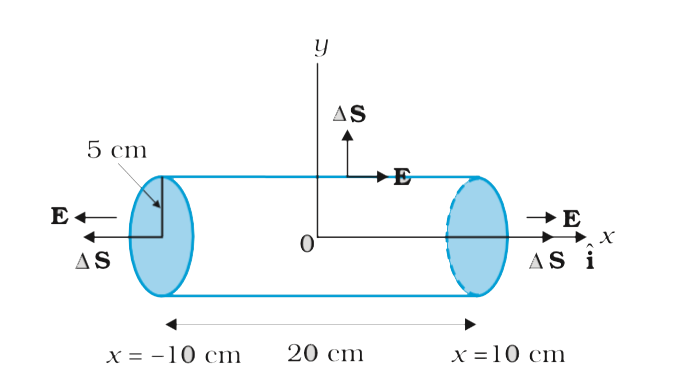
An electric field is uniform, and in the positive x-direction for po

The electric field in a region is given by $\to E = 200 ˆ i N / C for x > 0 and - 200 ˆ i N / C for x < 0$ . A closed cylinder of length 2m and cross-section area $10^{2} m^{2}$ is kept in such a way that the axis of cylinder is along X-axis and its centre coincides with origin. The total charge inside the cylinder is (Take $e_{0} = 8.25 \times 10^{- 12} C^{2} m^{2} . N$ )
Azero
B $1.86 \times 10^{- 5} C$
C $1.77 \times 10^{- 11} C$
D $35.4 \times 10^{- 8} C$
A unifrom electric field having a magnitude $E_{0}$ and direction along the positive X-axis exists. If the protential $V$ is zero at $x = 0$ , then its value at $X = + x$ will be
A $V (x) = - \frac{E_{0} x^{2}}{2}$
B $V (x) = \frac{E_{0} x^{2}}{2}$
C $V (x) = - \frac{E_{0} x}{2}$
D $V (x) = \frac{E_{0} x}{2}$
If $\to A = 3 ˆ i - 4 ˆ j$ and $\to B = 2 ˆ i + 16 ˆ j$ then the magnitude and direction of $\to A + \to B$ will be
A $5, {tan}^{- 1} (12 / 5)$
B $10, {tan}^{- 1} (5 / 12)$
C $13, {tan}^{- 1} (12 / 5)$
D $12, {tan}^{- 1} (5 / 12)$

A unifrom electric field having a magnitude $E_{0}$ and direction along the positive X-axis exists. If the protential $V$ is zero at $x = 0$ , then its value at $X = + x$ will be