An electron moves in a circular orbit at a distance from a proton with kinetic energy, E, to escape to infinity, the minimum energy which must be supplied to the electron is
E
2E
0.5E
E√2
The correct Answer is:A
To find the minimum energy that must be supplied to an electron moving in a circular orbit around a proton to escape to infinity, we can follow these steps:
Step 1: Understand the System
The electron is in a circular orbit around a proton, which means it is bound to the proton by electrostatic forces. The electron has a certain kinetic energy (E) while in this orbit.
Step 2: Determine Total Energy
The total energy (T) of the electron in a bound state (such as in a circular orbit) is given by the relationship between kinetic energy and potential energy. For an electron in orbit, the total energy can be expressed as:
T=K+U
where K is the kinetic energy and U is the potential energy.
In this case, the potential energy U is negative and is given by:
U=−2K
Thus, the total energy can be expressed as:
T=K−2K=−K
Given that the kinetic energy K=E, we can substitute this into the equation:
T=−E
Step 3: Energy Required to Escape
To escape to infinity, the electron must have a total energy of zero (since at infinity, the potential energy approaches zero). Therefore, the energy required to escape is equal to the negative of the total energy:
Energy required=−T=−(−E)=E
Conclusion
The minimum energy that must be supplied to the electron to escape to infinity is:
Energy required=E
Thus, the correct answer is E.
---
The electron is in a circular orbit around a proton, which means it is bound to the proton by electrostatic forces. The electron has a certain kinetic energy (E) while in this orbit.
The total energy (T) of the electron in a bound state (such as in a circular orbit) is given by the relationship between kinetic energy and potential energy. For an electron in orbit, the total energy can be expressed as:
T=K+U
where K is the kinetic energy and U is the potential energy.
U=−2K
Thus, the total energy can be expressed as:
T=K−2K=−K
T=−E
To escape to infinity, the electron must have a total energy of zero (since at infinity, the potential energy approaches zero). Therefore, the energy required to escape is equal to the negative of the total energy:
Energy required=−T=−(−E)=E
The minimum energy that must be supplied to the electron to escape to infinity is:
Energy required=E
Topper's Solved these Questions
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - ASSERTION AND REASON
10 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MATCH THE COLUMNS
4 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - Check point 12.3
15 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN
62 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
Similar Questions
An electron , initiallty at rest is released from a large distance from a proton (fixed in space ). The de-broglie wavelength of the electron when it is at distance r from proton is λ the ratio of its kinetic energy at this distance with the kinetic energy of the electron is ground stae of hydrogen atom (Bohr model) with the radius of its orbit being r, is α Pick the correct options (s)
View SolutionKinetic energy of electron in nth orbit is given by
View Solution
Knowledge Check
For a satellite moving in a circular orbit around the earth, the ratio of its potential energy to kinetic energy is
A1B−1C2D−2
An electron of charge e is moving in a circular orbit of radius r around a nucleus, at a frequency v. The magnetic moment associated with the orbital motion of the electron is
View SolutionIn the Bohr's orbit, what is the ratio of total kinetic energy and total energy of the electron
View SolutionAn electron and a proton are separated by a large distance and the electron approaches the proton with a kinetic energy of 2 eV. If the electron is captured by the proton to form a hydrogen atom in the ground state, what wavelength photon would be given off?
View SolutionAn electron and a proton are separated by a large distance and the electron approaches the proton with a kinetic energy of 2 eV. If the electron is captured by the proton to form a hydrogen atom in the ground state, what wavelength photon would be given off?
View SolutionThe wavelengths of electron waves in two orbits is 3:5. The ratio of kinetic energy of electrons will be
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
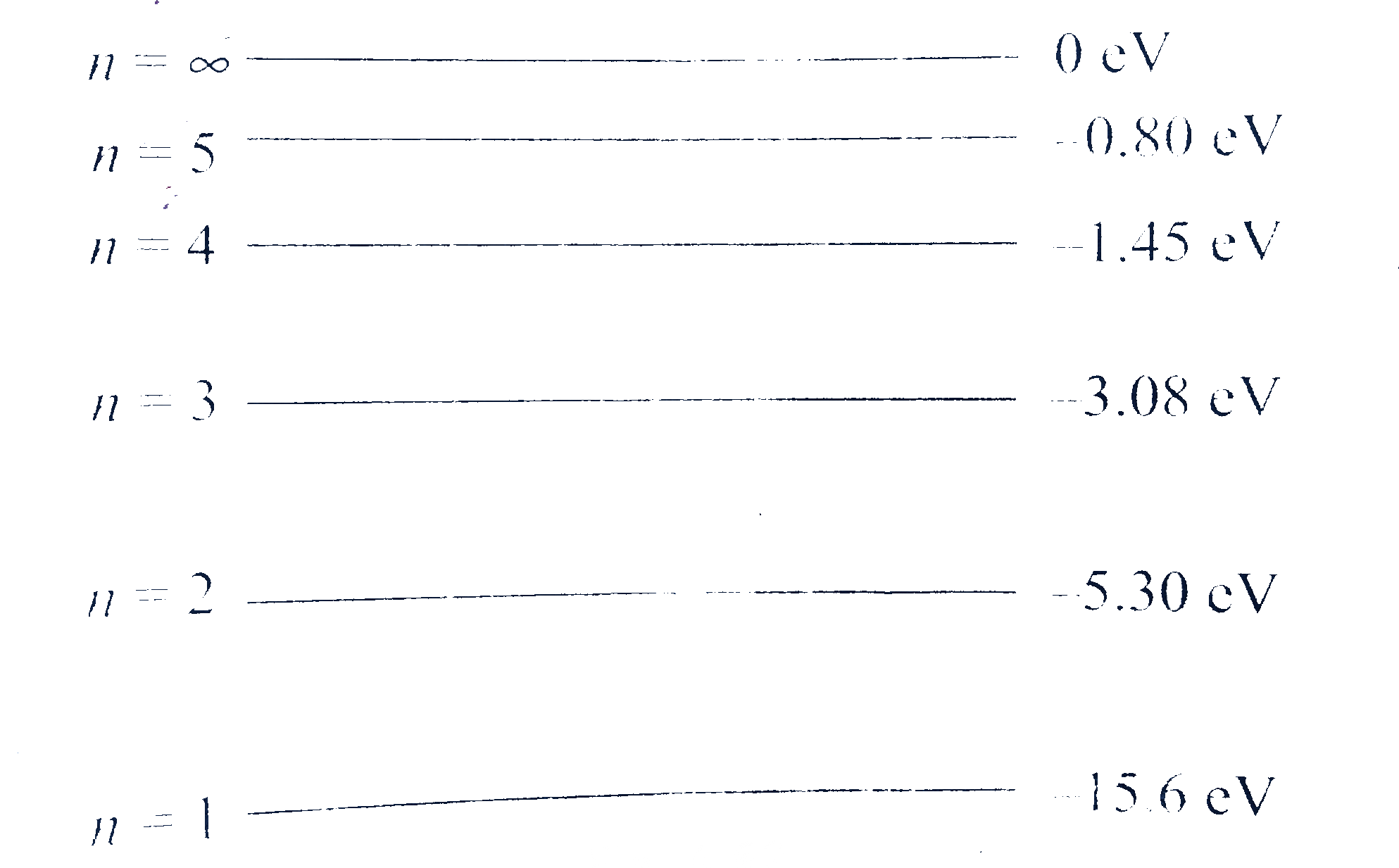
If an electron with initial kinetic energy 6eV is to interact with this hypothetical atom , what minimum energy will this electron carry after interaction?
View SolutionFor a satellite moving in a circular orbit around the earth, the ratio of its total mechanical energy to kinetic energy
View Solution
