An electron of mass 'm' is moving with initial velocity $v_{0} \hat{i}$ in an electric field $\vec{E} = E_{0} \hat{i}$ Which of the following is correct de Broglie wavelength at a given time t $(λ_{0}$ is initial de Broglie wavelength ).

A

$\frac{λ_{0}}{(1 + \frac{e E_{0}}{m λ_{0}} t)}$

B

$\frac{λ_{0}}{(1 + \frac{e E_{0}}{m v_{0}} t)}$

C

$\frac{h}{(1 + \frac{m v_{0}_0}{E v_{0}} t)}$

D

$\frac{h}{(1 + \frac{e E_{0}}{m v_{0}} t)}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To find the correct de Broglie wavelength of an electron moving in an electric field, we can follow these steps:
1. Identify the Given Parameters:
- Mass of the electron: $m$
- Initial velocity of the electron: $_{0} = v_{0}^i$
- Electric field: $\to E = E_{0}^i$
- Charge of the electron: $e$ (approximately $1.6 \times 10^{- 19}$ C)
2. Calculate the Force on the Electron:
- The force $\to F$ acting on the electron due to the electric field is given by:
$\to F = e \to E = e E_{0}^i$
3. Determine the Acceleration of the Electron:
- Using Newton's second law, $\to F = m \to a$ :
$m \to a = e E_{0}^i ⟹ \to a = \frac{e E_{0}}{m}^i$
4. Use the Kinematic Equation to Find the Velocity at Time $t$ :
- The final velocity $\to v$ after time $t$ can be calculated using the equation:
$\to v = \to u + \to a t$
- Here, $\to u = v_{0}^i$ and $\to a = \frac{e E_{0}}{m}^i$ :
$\to v = v_{0}^i + (\frac{e E_{0}}{m}) t^i = (v_{0} + \frac{e E_{0}}{m} t)^i$
5. Calculate the De Broglie Wavelength:
- The de Broglie wavelength $λ$ is given by:
$λ = \frac{h}{p}$
- Where $p$ is the momentum, $p = m v$ :
$p = m (v_{0} + \frac{e E_{0}}{m} t) = m v_{0} + e E_{0} t$
- Therefore, the de Broglie wavelength becomes:
$λ = \frac{h}{m v_{0} + e E_{0} t}$
6. Express the Wavelength in Terms of Initial Wavelength $λ_{0}$ :
- The initial de Broglie wavelength $λ_{0}$ is:
$λ_{0} = \frac{h}{m v_{0}}$
- Thus, we can express $λ$ as:
$λ = λ_{0} \cdot \frac{1}{1 + \frac{e E_{0} t}{m v_{0}}}$
7. Final Expression for the Wavelength:
- Rearranging gives:
$λ = λ_{0} (1 + \frac{e E_{0} t}{m v_{0}})$
Conclusion:
The correct de Broglie wavelength at a given time $t$ is:
$λ = λ_{0} (1 + \frac{e E_{0} t}{m v_{0}})$

|

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Which of the following is correct regarding de-Broglie wavelength?
AEvery moving particle has a wave associated with it and is given by de-Broglie wavelength $λ = \frac{h}{P} = \frac{h}{m v} = \frac{h}{\sqrt{2 m K}}$
BWhether wave behaviour will dominate or particle behaviour, it depends on the dimension of object with which particle interacts
CThe variation of de-Broglie wavelength $λ$ with momentum of particle p

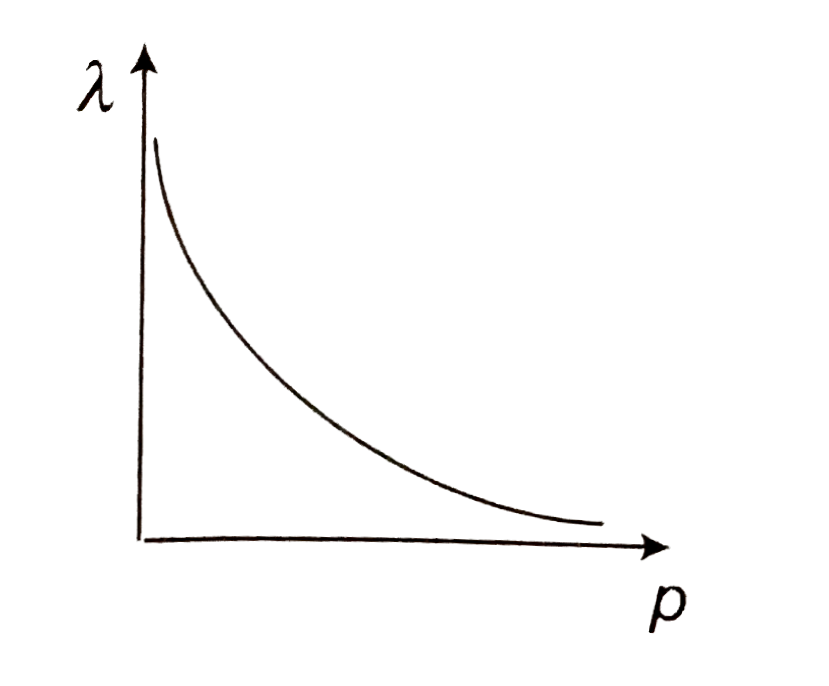DAll option are correct
An electron (mass m) with an initial velocity $\to v = v_{0} ˆ i$ is in an electric field $\to E = E_{0} ˆ j$ . If $λ_{0} h / m v_{0}$ . It's de-broglie wavelength at time t is given by
A $λ_{0}$
B $λ_{0} \sqrt{1 + \frac{e^{2} E_{0}^{2} t^{2}}{m^{2} v_{0}^{2}}}$
C $\frac{λ_{0}}{1 + \frac{e^{2} E_{0}^{2} t^{2}}{m^{2} v_{0}^{2}}}$
D $\frac{λ_{0}}{\sqrt{1 + (\frac{e^{2} E_{0}^{2} t^{2}}{m^{2} v_{0}^{2}})}}$
An electron is moving with an initial velocity $\to v = v_{0} ˆ i$ and is in a magnetic field $\to B = B_{0} ˆ j$ . Then it's de-Broglie wavelength
Aremains constant
Bincreases with time
Cdecreases with time
Dincreases and decreases periodically

MODERN PUBLICATION-DUAL NATURE OF RADIATION AND MATTER -COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( A - Multiple Choice Questions))

Home
Ask Doubt
Profile