An emf E=100sin314tV is applied across a pure capacitor of 637(μ)F. Find
(a) the instantaneous current I
(b) the instantaneous power p
(c ) the frequency of power
(d) the maximum energy stored in the capacitor.
Given E=100sin(314t)
we have ω=314⇒2(π)f=100π⇒f=50Hz
Capacitive reactance:
(Xc)=1ωC=1314×637×10−6=5Ω
since there is pure capacitor in the circuit, so current leads emf by (ϕ)=(π)/2
i−i0sin(ωt+ϕ0=i0sin[314t+(π)/(2)]
=E0XCcos(314t)=1005cos(314t)=20cos(314t)
(b) Instantaneous power is given by
p=EI=100sin(314t)×20cos(314t)=1000sin(628t)
(c ) from the expression of power above, we can calculate the frequency of power becomes maximum and minimum two times.
(d) We know that energy in the capacitor is U=12CE2. Energy stored in the cpacitor will be maximum when E=(E0).
U0=12CE20=12(637×10−6)(100)2=3.185J.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 5.1
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - QUESTION BANK
65 Videos
- OSCILLATIONSBOOK - CENGAGE PHYSICSCHAPTER - OSCILLATIONSEXERCISE - QUESTION BANK
39 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
The instantaneous current from an a.c source is I=5sin100πt What is the frequency of a.c. ? What is the rms value of current ?
View SolutionA capacitance C, a resistance R and an emf (ε)are connected in series at t=0.What is the maximum value of (a) the potential difference across the resistor, (b) the current in the circuit,(c )the potential difference across the capacitor, (d) the energy stored in the capacitor ,(e)the power delivered by the battery and (f) the power converted int heat.
View Solution
Knowledge Check
An a.c. emf of e=220 sin ω t is applied across the capacitor, the power consumption is
A0B55 WC110 WD220 WAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :A10 J/sB20 J/sC40 J/sD5 J/sThe alternating emf of e=e0 sin ωt is applied across capacitor C. the current through the circuit is given by
AI=I0sinωtBI=I0sin(ωt+π2)CI=I0sin(ωt−π2)DI=I0sin(ωt−π)
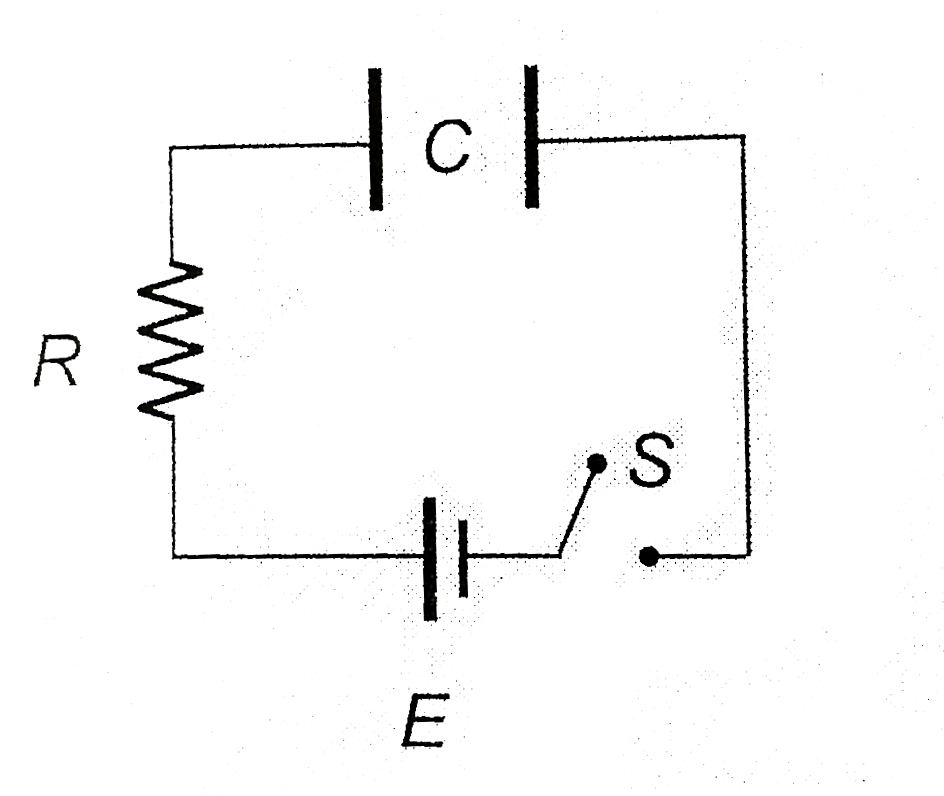
At t=0 switch S is closed . Find
(a) charge on capacitor after one time constant
(b) the time when p.d. across resistance equals p.d. across capacitance
(c ) maximum energy stored in capacitor.
View SolutionAn alternating voltage given by V = 240 sin 314 t is connected across a pure resistor of 100 ohm. Find
(a) the frequency of the source.
(b) the rms current through the resistor.
View SolutionThe instantaneous value of current in an A.C. circuit is I=2sin(100πt+π/3)A .The current will be maximum for the first time at
View SolutionA capacitor of capacitance 12(μ)Fis connected to a battery of emf 6.00V and internal resistance 1.00(Ω)through resistanceless leads. 12.0(mu)s after the connections are made, what will be (a) the current in the circuit, (b)the power delivered by the battery ,(c)the power dissipated in heat and (d)the rate at which the energy stored in the capacitor is increasing.
View SolutionAn L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4×10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View Solution
