An emf E=100sin314tV is applied across a pure capacitor of 637μF. Find
(a) the instantaneous current I
(b) the instantaneous power P
(c ) the frequency of power
(d) the maximum energy stored in the capacitor.
(a) Current leads over applied emf by π2 in a capacitance .
∴I0=ε0XC=ε0×ωC where ε0=100V
I0=(100)×(314)×(500×10−6)
I0=314×5×10−2=15.70A
∴I=I0sin(ωt+π2) where ω=314rads−1
I=(15.70)cosωtA=15.70cos314tA
(b) Instantaneous power
P=EI
P=(100sin314t)(15.70cosωt)
=1570(sin314t)(cos314t)
=785×(2sin314cos314t)
=785sin628tW
(c ) Frequency of power
vP=ω2π=6282×3.14=100Hz
(d) Maximum energy stored in capacitor
U0=12Cε20
U0=12×(500×10−6)×(100)2
U0=2.5J
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (MAGNETIC FLUX)1videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
- BOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (FARADAY.S LAW (INDUCED EMF AND CURRENT)27videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
- BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs30videos
DUAL NATURE OF MATTER AND RADIATION
- BOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - AIPMT/NEET(MCQs)15videos
ELECTROMAGNETIC WAVES
Similar Questions
An emf E=100sin314tV is applied across a pure capacitor of 637(μ)F. Find
(a) the instantaneous current I
(b) the instantaneous power p
(c ) the frequency of power
(d) the maximum energy stored in the capacitor.View SolutionThe instantaneous current from an a.c source is I=5sin100πt What is the frequency of a.c. ? What is the rms value of current ?
View Solution
Knowledge Check
- Question 1 - Select One
An a.c. emf of e=220 sin ω t is applied across the capacitor, the power consumption is
A0B55 WC110 WD220 W - Question 2 - Select One
A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent I(t), lags voltage V(t) by 90∘BOver a full cycle the capacitor C does not consume any energy from the voltage source.CCurrent I(t) is in phase with voltage V(t)DCurrent I(t) leads voltage V(t) by 180∘ - Question 3 - Select One
An uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :A10 J/sB20 J/sC40 J/sD5 J/s
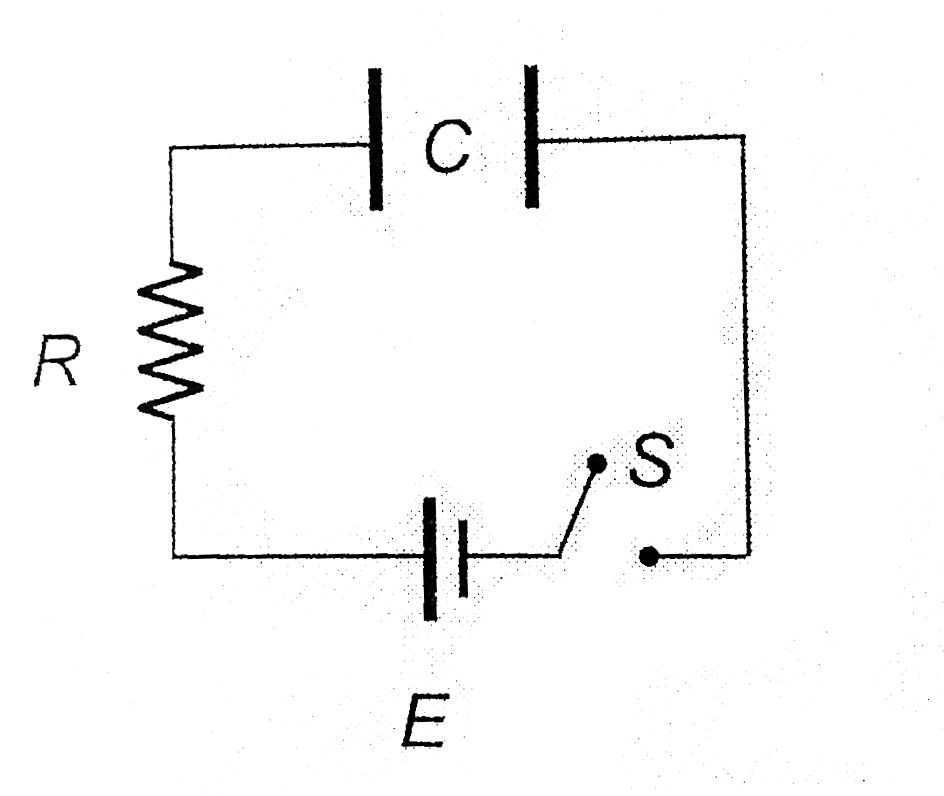
At t=0 switch S is closed . Find
(a) charge on capacitor after one time constant
(b) the time when p.d. across resistance equals p.d. across capacitance
(c ) maximum energy stored in capacitor.View SolutionAn alternating voltage given by V = 240 sin 314 t is connected across a pure resistor of 100 ohm. Find
(a) the frequency of the source.
(b) the rms current through the resistor.View SolutionA capacitance C, a resistance R and an emf (ε)are connected in series at t=0.What is the maximum value of (a) the potential difference across the resistor, (b) the current in the circuit,(c )the potential difference across the capacitor, (d) the energy stored in the capacitor ,(e)the power delivered by the battery and (f) the power converted int heat.
View SolutionA small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionThe alternating emf of e=e0 sin ωt is applied across capacitor C. the current through the circuit is given by
View Solution

