An equibiconvex lens has a focal length of 20 cm. A ball pin of length 5 cm is placed on one side of the lens, such that the mid point of the pin is at a distance of 30 cm from the centre of the lens. Calculate the size of the image of the pin and its magnification f = 20 cm l = 5 cm. Solution in Kannada
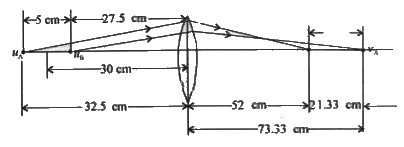
1f=1−u+1v
Given : −uA=27.5cm
1f=1−uA+1vA
120=127.5+1vA
120−127.5=1vA
vA=73.33cm
1f=1−uB+1vB
−uB=32.5cm
120−132.5=1vB
1vB=12.5650
vB=52cm
vA−vB=21.33cm
magnification m=v1v0=21.335=4.266
Topper's Solved these Questions
- BOOK - SUBHASH PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - FIVE MARKS QUESTIONS WITH ANSWERS10videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - SUBHASH PUBLICATIONCHAPTER - QUESTION PAPER 2019EXERCISE - PART - C6videos
QUESTION PAPER 2019
- BOOK - SUBHASH PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - OPTIONAL NUMERICALS WITH SOLUTIONS6videos
SEMICONDUCTOR ELECTRONICS
Similar Questions
S.T f=R2 in the case of a spherical mirror where symbols have their usual notations
07:07View SolutionDerive an expression for potential energy of electric - di-pole placed in a n uniform electric field .
03:33View SolutionIf the peak value voltage in the secondary output ac voltage is 12V, then what will be the average DC in the case of HWR and FWR?
05:15View SolutionA pin of length 2.00 cm is placed perpendicular to the principal axis of a converging lens. An inverted image of size 1.00 cm is formed at a distance of 40.0 cm from the pin. Find the focal length of the lens and its distance from the pin.
06:14View SolutionA pin of length 2.0 cm lies along the principal axis of a converging lens, the centre being at a distance of 11 cm from the lens. The focal length of the lens is 6 cm. Find the size of the image.
07:05View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart. If a pin of length 2.0 cm is placed 30 cm from the lens farther away from the mirror, where will the final image form and what will be the size of the final image ?
04:59View SolutionA concave lens has focal length of 20 cm . At what distance from the lens a 5 cm tall object be placed so that it forms an image at 15 cm from the lens? Also, calculate the size of the image formed.
07:33View Solution(a) A magnifying lens has a focal length of 10 cm, (a) Where should the object be placed if the image is to be 30 cm from the lens ? (b) What will be the magnification ? (b). A pin length 2.00 cm is placed perpendicular to the principal axis of a converging lens. An inverted image of size 1.00 cm is formed at a distance of 40.0 cm fromthe pin. Find focal length of the lens and its distance from the pin.
06:56View Solutionएक उत्तल लेन्स की फोकस-दुरी 20 सेमी है। इस लेन्स के आगे 2 सेमी लम्बी एक पिन 10 सेमी दूर रखी है। पिन के प्रतिबिम्ब की लम्बाई ज्ञात कीजिये।
02:28View Solutionएक उत्तल लेन्स की फोकस दुरी 20 सेमी है । इस लेन्स के सामने 2 सेमी लम्बी एक पिन 10 सेमी दुरी रखी है । पिन के प्रतिबिम्ब की लम्बाई ज्ञात कीजिए ।
02:01View Solutionएक उत्तल लेंस के मुख्य अक्ष के अनुदिश एक 2.0 cm लंबी पिन रखी हैं । पिन का मध्यबिंदु लेंस से 11 cm की दूरी पर हैं । लेंस की फोकस - दूरी 6.0 cm हैं । पिन के प्रतिबिंब की लंबाई निकालें ।
03:31View SolutionThe focal length of convex lens is 20 cm. If an object of height 4 cm is placed at a distance of 30 cm from the lens, find:
The magnification produced by the lens.03:34View SolutionAn index pin of height 3 cm is kept at a distance of 15 cm from a convex lens of focal length 10 cm. The image is obtained on a screen placed on the other side of the lens. What is the height and nature of the image ?
05:47View SolutionA concave lens has focal length of 20 cm . At what distance from the lens a 5 cm tall object be placed so that it forms an image at 15 cm from the lens ? Calculate the size of the image formed.
05:22View SolutionA pin of length 2.00 cm is placed perpendicular to the principal axis of a converging lens. An inverted image of size 1.00 cm is formed at a distance of 40.0 cm from the pin. Find the focal length of the lens and its distance from the pin.
View Solution

