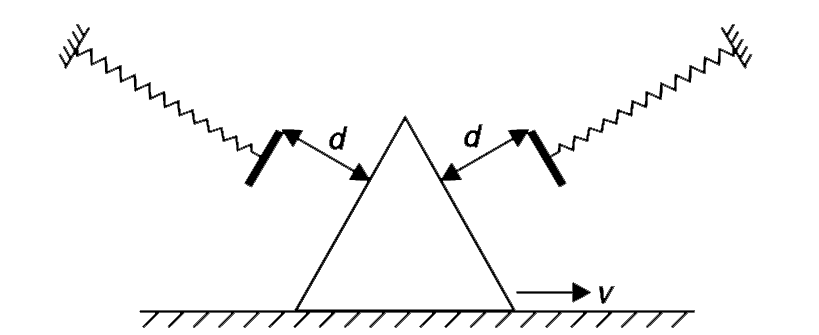
An equilateral prism of mass m is kept on a smooth table between two identical springs each having a force constant of k. The two springs have their lengths perpendicular to the inclined faces of the prism and are constrained to remain straight. The ends of the springs have light pads aligned parallel to the faces of the prism, and distance between pads and the incline faces is d. The prism is imparted a velocity v to the right. Find time period of its oscillation.
The correct Answer is:8d√3v+4π√m3k
Step by step video, text & image solution for An equilateral prism of mass m is kept on a smooth table between two identical springs each having a force constant of k. The two springs have their lengths perpendicular to the inclined faces of the prism and are constrained to remain straight. The ends of the springs have light pads aligned parallel to the faces of the prism, and distance between pads and the incline faces is d. The prism is imparted a velocity v to the right. Find time period of its oscillation. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- ROTATIONAL MOTIONBOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS
159 Videos
- SURFACE TENSIONBOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension
33 Videos
Similar Questions
Knowledge Check
If the lateral faces perpendicular to the base of a prism, then it is called a ……….. Prism.
ARightBTriangularCQuadrangularDPentagonalAn ideal spring of force constant k is broken into two identical pieces. The force constant of each of the smaller springs is :
Ak/2BkC2kD4kAn ideal spring of force constant k is broken into two identical pieces. The force constant of each of the smaller springs is :
Ak/2BkC2kD4k
Height of a prism the perpendicular distance the ends of a prism is called the height of the prism.
View SolutionLength of a prism the length of a prism is the portion of the axis that lies between the parallel ends.
View SolutionIf a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
View SolutionA spring of certain length and having spring constant k is cut into two pieces of length in a ratio 1:2. The spring constants of the two pieces are in a ratio :
View SolutionLight falls on a prism grazing along first surface of a prism and the emergent ray is normal to the 2nd face of the prism. If D is angle of deviation then the refracting angle of the prism i
View Solution
