An ideal gas is made to undergo a process T=T0eαV where T0 and α are constants. Find the molar specific heat capacity of the gas in the process if its molar specific heat capacity at constant volume is Cv. Express your answer as a function of volume (V).
The correct Answer is:C=Cv+RαV
Step by step video, text & image solution for An ideal gas is made to undergo a process T = T_(0)e^(alpha V) where T_(0) and alpha are constants. Find the molar specific heat capacity of the gas in the process if its molar specific heat capacity at constant volume is C_(v). Express your answer as a function of volume (V). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 2
34 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Videos
- FLUIDSBOOK - ARIHANTCHAPTER - FLUIDSEXERCISE - All Questions
70 Videos
Similar Questions
A container has a tight fitting movable piston which can slide without friction. The compartment containing spring has vacuum and to the left of the piston there is diatomic gas. If vacuum is created in the right compartment also the piston touches the right wall and the spring is relaxed. Find the heat capacity of the system neglecting the heat capacities of the material of spring, container and the piston. Express your answer in terms of P0,V0 and T0.
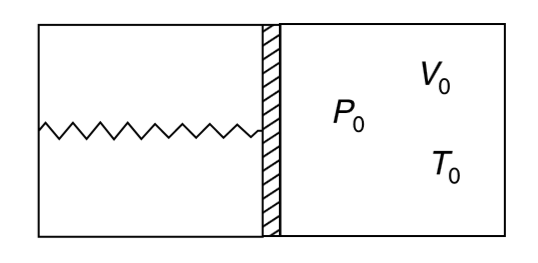
View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
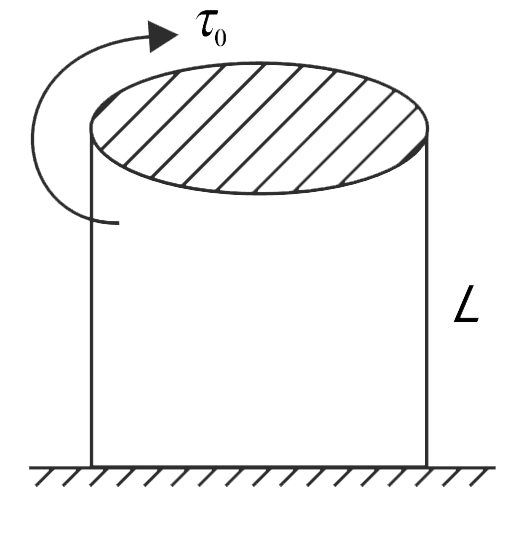
View SolutionA metal cylinder of length L and radius R is fixed rigidly to ground with its axis vertical. A twisting torque τ0 is applied along the circumference at the top of the cylinder. This causes an angular twist of θ0 (rad) in the top surface. Calculate the shear modulus of elasticity (η) of the material of the cylinder.
View SolutionWe know that the atmospheric pressure on the surface of the earth is because of weight, of the air. The radius of the earth is 6400 km and atmospheric pressure on the sruface of earth is 1×105N/m2. Estimate the mass of the earth's atmosphere assuming that acceleration due to gravity remains constant at 10m/s2 over the entrie height of the atmospehre.
View SolutionCvandCp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionAn ideal gas has a molar heat capacity C_v at constant volume. Find the molar heat capacity of this gas as a function of its volume V , if the gas undergoes the following process : (a) T = T_0 e^(alpha v) , (b) p = p_0 e^(alpha v) , where T_0, p_0 , and alpha are constants.
View SolutionOne mole of an ideal gas with heat capacity at constant pressure Cp undergoes the process T=T0+αV, where T0 and α are constants. Find :
(a) heat capacity of the gas as a function of its volume ,
(b) the amount of heat transferred to the gas, if its volume increased from V1 to V2.
View SolutionFor an ideal monoatomic gas, molar heat capacity at constant volume (C_(v)) is
View SolutionThe molar heat capacity of an ideal gas in a process varies as C=C_(V)+alphaT^(2) (where C_(V) is mola heat capacity at constant volume and alpha is a constant). Then the equation of the process is
View SolutionAn ideal gas with heat capacity at constant volume C_(V) undergoes a quasistatic process described by P V^(alpha) in a P-V diagram, where alpha is a constant. The heat capacity of the gas during this process is given by-
View SolutionAn ideal gas has molar heat capecity Cv at constant volume. The gas undergoes a process where in the temperature changes as T=T0(1+αV2), T and V are temperature and volume respectively, T0andα are positive constant.The molar heat capecity C of the gas is given as C=Cv+Rf(V), where, f (V) is a funtion of volume. The expression for f (V) is
View SolutionCpandCv denote the molar specific heat capacities of a gas at constant volume and constant pressure respectively. Then
View SolutionAn ideal gas has a molar heat capacity Cv at constant volume. Find the molar heat capacity C, at constant volume. Find the molar heat capacity of this gas as a function of its volume 'V', if the gas undergoes the following process :
T=T0eαV
View SolutionAn ideal gas has a molar heat capacity Cv at constant volume. Find the molar heat capacity C, at constant volume. Find the molar heat capacity of this gas as a function of its volume 'V', if the gas undergoes the following process :
P=P0eαV
View SolutionOne mole of an ideal gas with heat capacity at constant pressure C_p undergoes the process T=T_0 + alpha V, where T_0 and ' alpha ' are constant. Find heat capacity of the gas as function of its volume,
View Solution
