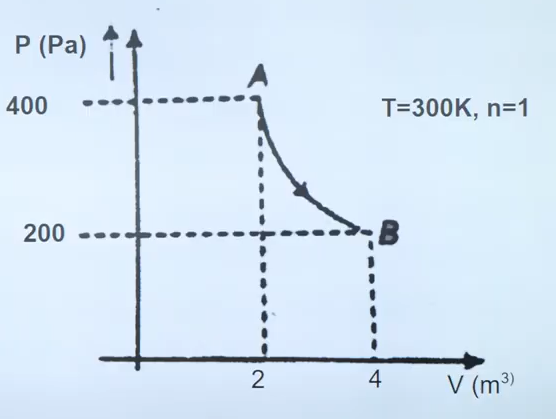
An ideal gas system undergoes an isothermal process, then the work done during the process is
nRTInV2V1
nRTInV1V2
2nRTInV2V1
2nRTInV1V2
The correct Answer is:A
To find the work done during an isothermal process for an ideal gas, we can follow these steps:
Step 1: Understand the Isothermal Process
In an isothermal process, the temperature (T) remains constant. For an ideal gas, this means that the product of pressure (P) and volume (V) is constant, given by the equation:
PV=nRT
where n is the number of moles of gas and R is the universal gas constant.
Step 2: Express Work Done
The infinitesimal work done (dW) during a small change in volume (dV) can be expressed as:
dW=PdV
To find the total work done (W), we need to integrate this expression over the volume change from V1 to V2:
W=∫V2V1PdV
Step 3: Substitute for Pressure
Since we know that P=nRTV for an ideal gas during an isothermal process, we can substitute this into our work equation:
W=∫V2V1nRTVdV
Step 4: Perform the Integration
Now we can perform the integration:
W=nRT∫V2V11VdV
The integral of 1V is:
∫1VdV=lnV
Thus, we have:
W=nRT(lnV)V2V1
This evaluates to:
W=nRT(lnV2−lnV1)
Step 5: Simplify the Expression
Using the properties of logarithms, we can simplify this to:
W=nRTln(V2V1)
Final Result
Therefore, the work done during an isothermal process for an ideal gas is given by:
W=nRTln(V2V1)
In an isothermal process, the temperature (T) remains constant. For an ideal gas, this means that the product of pressure (P) and volume (V) is constant, given by the equation:
PV=nRT
where n is the number of moles of gas and R is the universal gas constant.
The infinitesimal work done (dW) during a small change in volume (dV) can be expressed as:
dW=PdV
To find the total work done (W), we need to integrate this expression over the volume change from V1 to V2:
W=∫V2V1PdV
Since we know that P=nRTV for an ideal gas during an isothermal process, we can substitute this into our work equation:
W=∫V2V1nRTVdV
Now we can perform the integration:
W=nRT∫V2V11VdV
The integral of 1V is:
∫1VdV=lnV
Thus, we have:
W=nRT(lnV)V2V1
This evaluates to:
W=nRT(lnV2−lnV1)
Using the properties of logarithms, we can simplify this to:
W=nRTln(V2V1)
Therefore, the work done during an isothermal process for an ideal gas is given by:
W=nRTln(V2V1)
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Heat Engines
4 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Refrigerators And Heat Pumps
10 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Thermodynamic State Variables
2 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTIPSCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
An ideal gas undergoes isothermal expansion at constant pressure . During the process.
AEnthalpy remains constant but entropy increasesBEnthalpy decreases but entropy increasesCEnthalpy increases but entropy decreasesDBoth enthalpy and entropy remain constantIn an isothermal process for ideal gas.
Aq=0 and ΔE=0Bq≠0 and ΔE=0Cq=0 and ΔE≠0Dq≠0 and ΔE≠0For an ideal gas, in an isothermal process
AHeat content remains constantBHeat content and temperature remain constantCTemperature remains constantDNone of the above
Work Done In Isothermal Processes
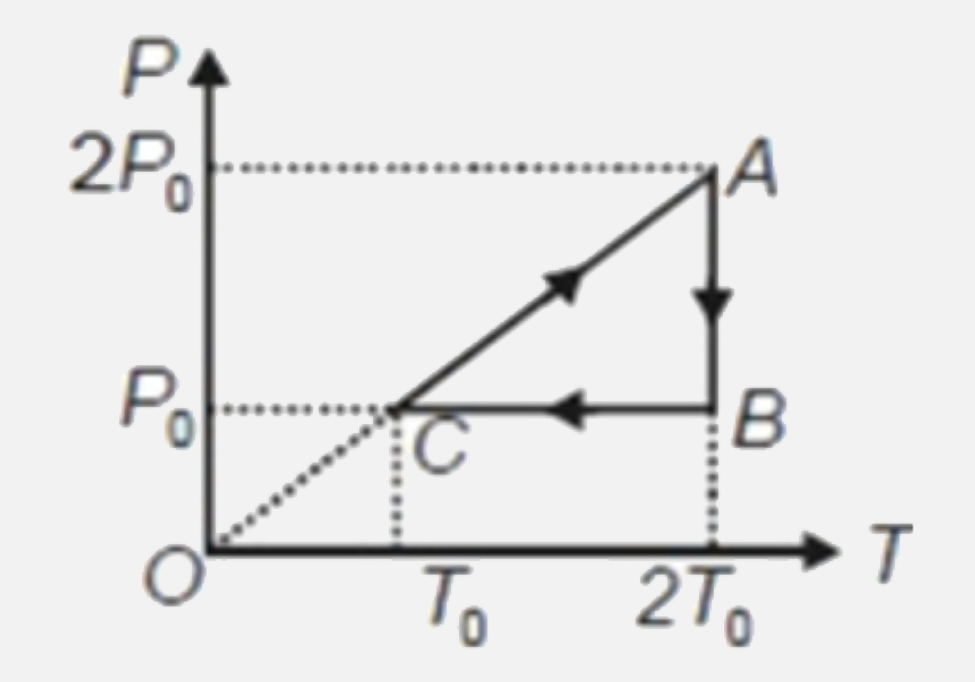
View SolutionTwo moles of a monoatomic ideal gas undergoes a process AB as shown in the figure. Then, find the work done during the process in Joule.
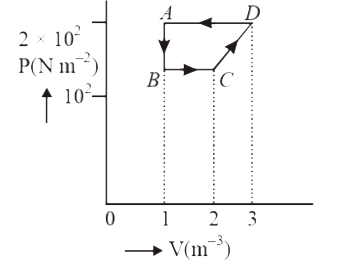
View SolutionThe P-V diagram of a gas system undergoing cyclic process is shown here. The work done during isobaric compression is
View SolutionIn an isothermal process for an ideal gas
View SolutionIn an isothermal process for an ideal gas
View Solution