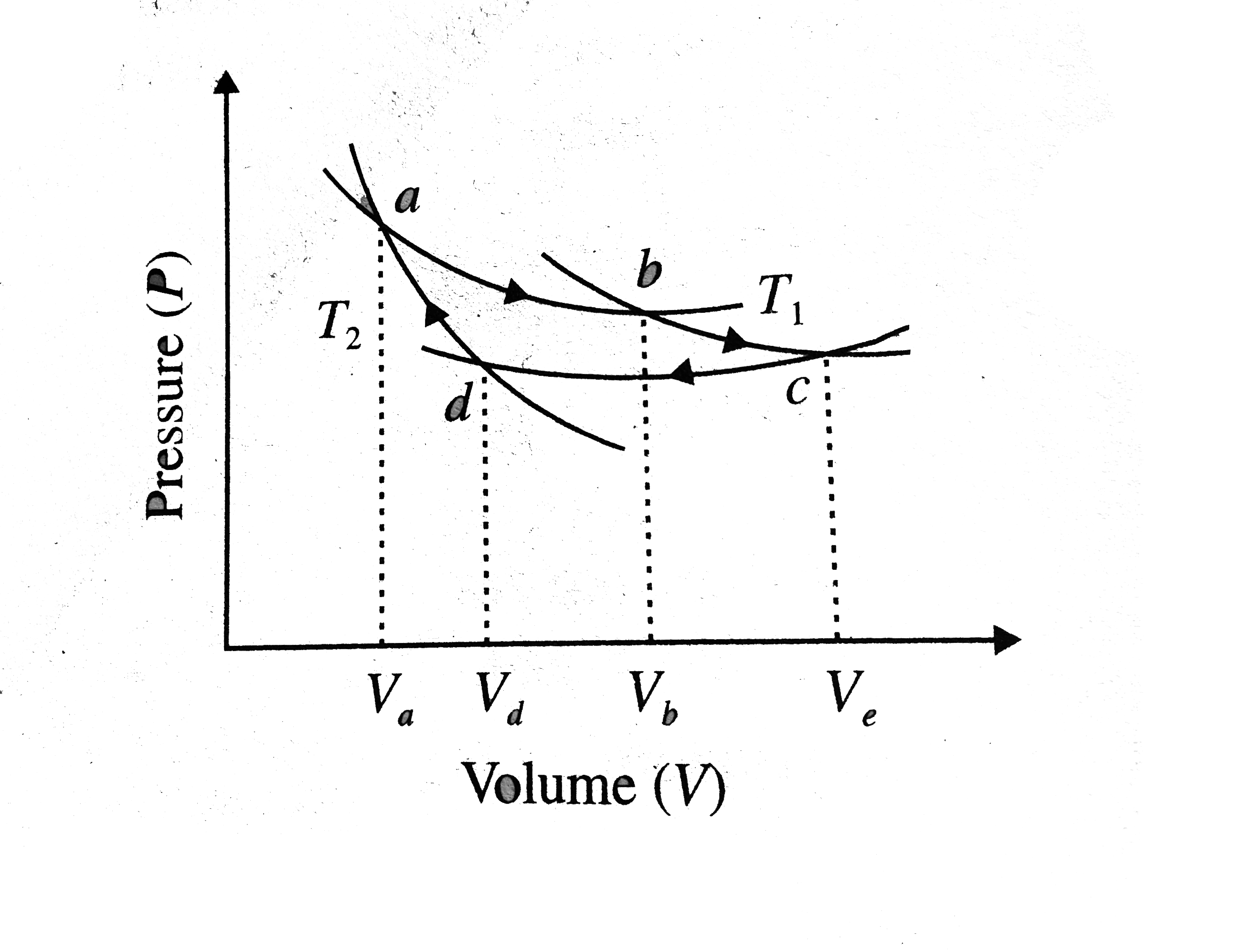An ideal gas undergoes cyclic process ABCDA as shown in given p−V diagram. The amount of work done by the gas is
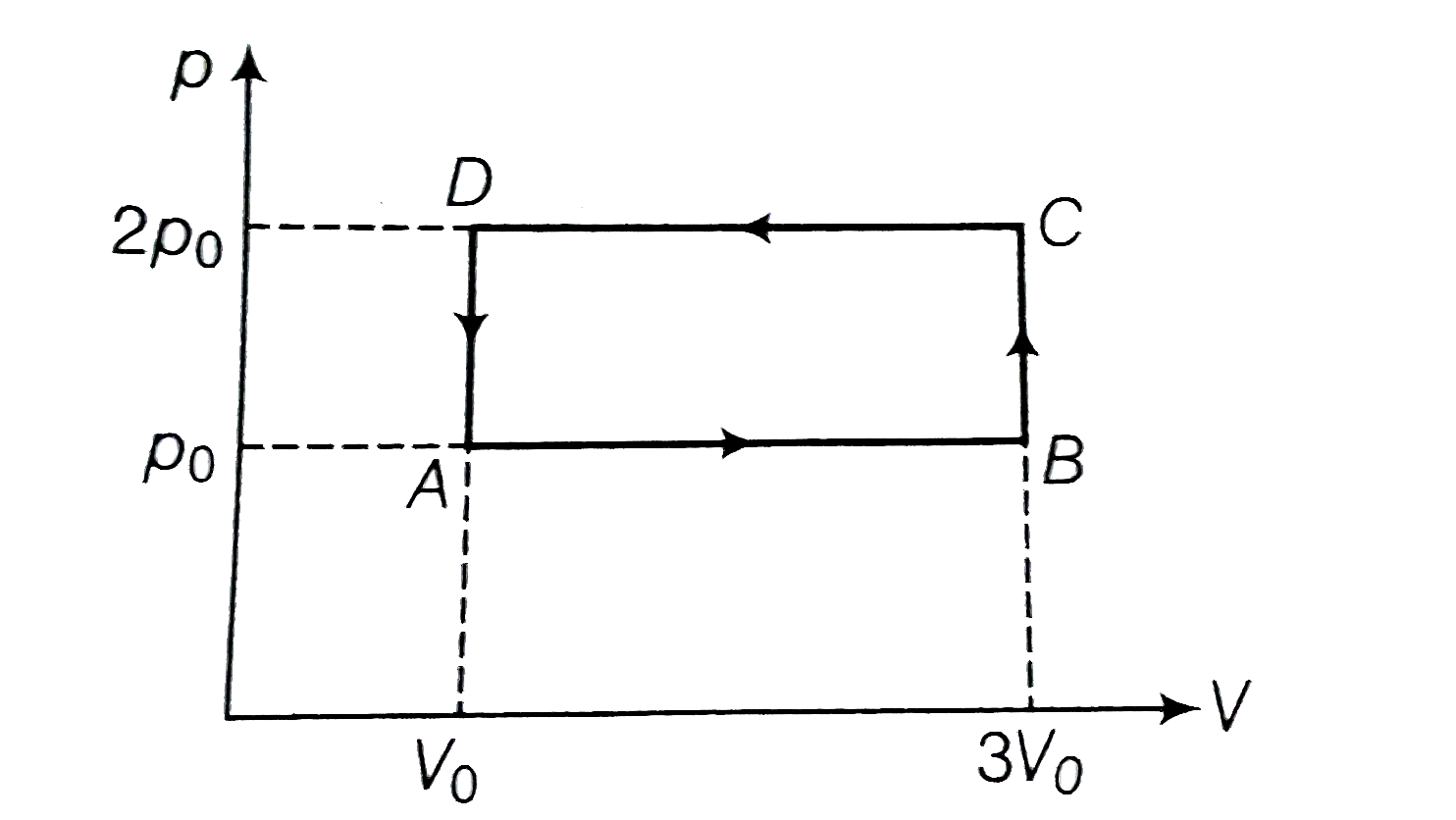
6P0V0
−2P0V0
+2P0V0
+4P0V0
The correct Answer is:B
Work done =change in pressure × change in volume =(2P0−P0)(3V0−V0)=2P0V0)
since the cyclic process is anticlockwiese work done by the gas is negative i.e −2P0V0.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HOTs
8 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion & Reason
15 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
One mole of an ideal gas undergoes a cyclic process ABCDA as shown in the P-V diagram, The net work done in the process is
(1 atm=10^(6) dyne cm^(-2)) A500 JB700 JC800 JD900 J
A500 JB700 JC800 JD900 JA cyclic process ABCA is shown in the V−T diagram process on the P−V
 A
A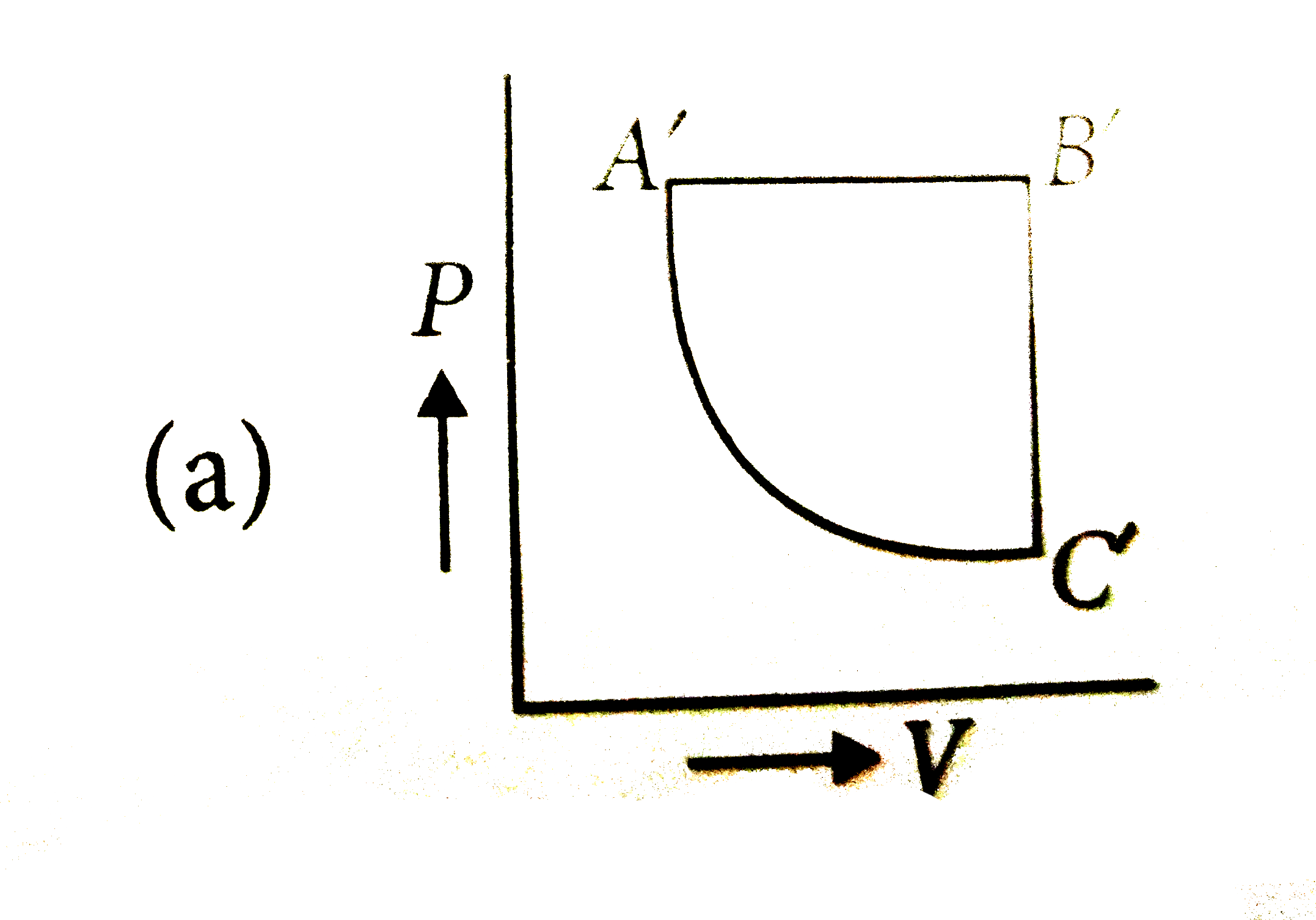 B
B C
C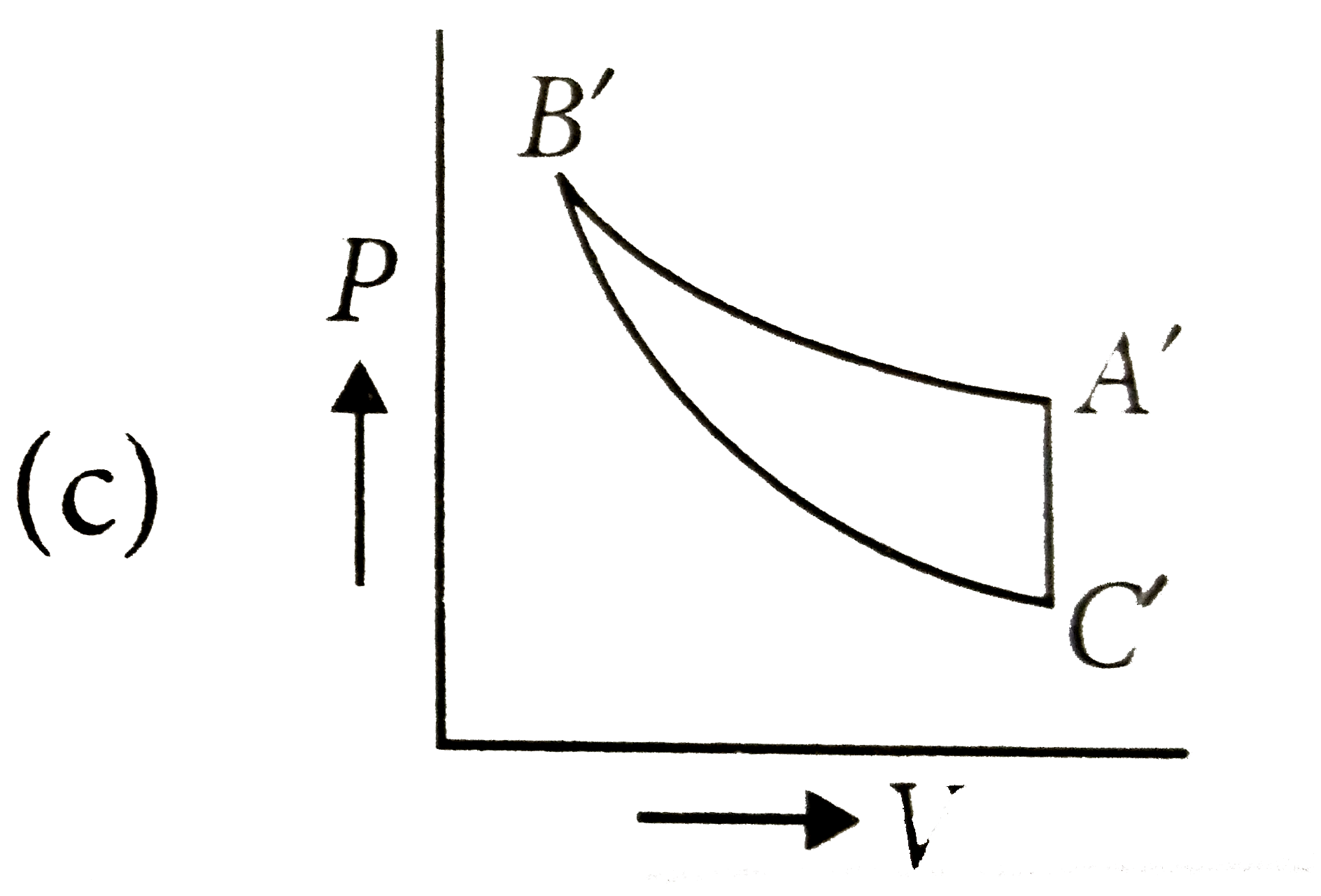 D
D
One mole of an ideal gas has an interal energy given by U=U0+2PV , where P is the pressure and V the volume of the gas. U0 is a constant. This gas undergoes the quasi− static cyclic process ABCD as shown in the U−V diagram. The work done by the ideal gas in the process AB is

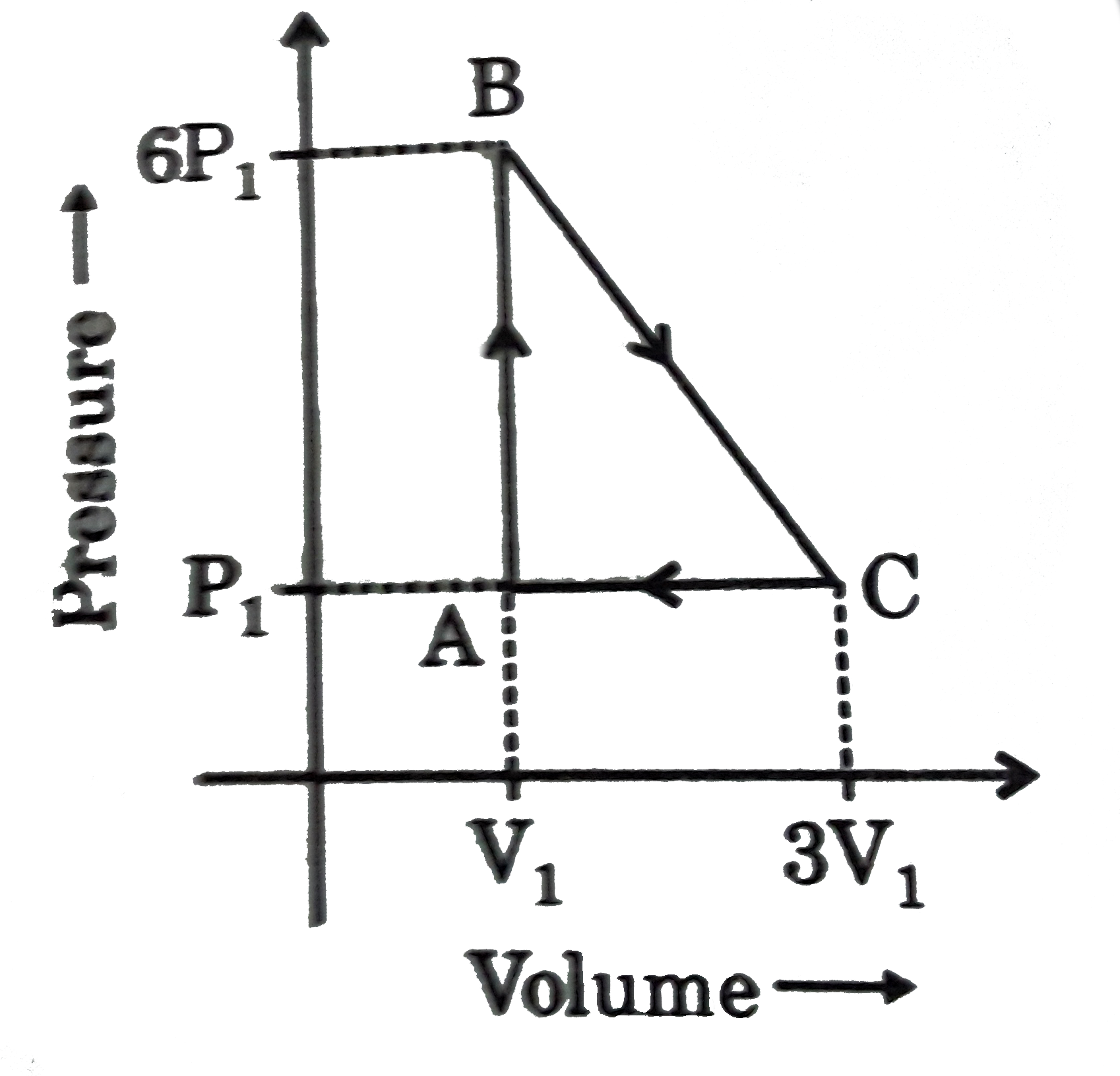
View SolutionAn ideal gas is taken around the cycle ABCA as shown in the P-V diagram. The total work done by the gas during the cycle is
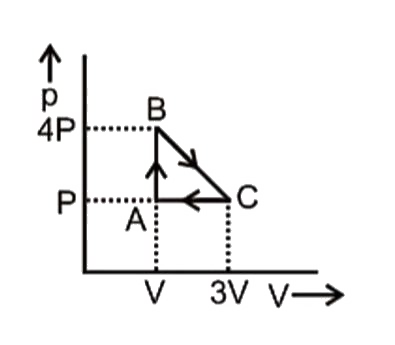
View SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
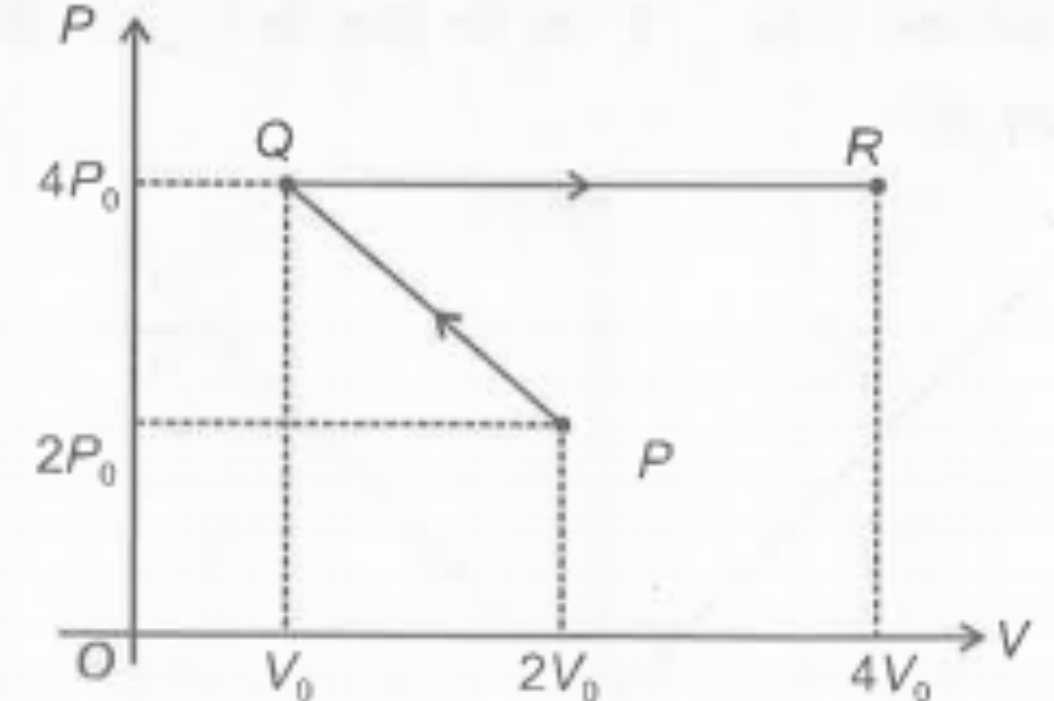
View SolutionAn ideal gas is taken around the cycle ABCA as shown in P-V diagram. The net work done by the gas during the cycle is equal to :
View SolutionAn ideal gas is taken around the cycle ABCA as shown in P-V diagram. The net work done by the gas during the cycle is equal to :

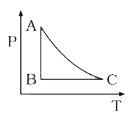
View SolutionAn ideal gas undergoes a cyclic process as shown in the given P-T diagram, where AC is adiabatic. The process is also represented by:
View Solution