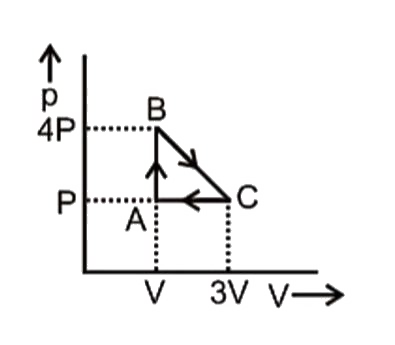
An ideal gas undergoes cyclic process ABCDA as shown in givend p−V diagram. The amount of work done by the gas is
6P0V0
−2P0V0
+2P0V0
+4P0V0
The correct Answer is:B
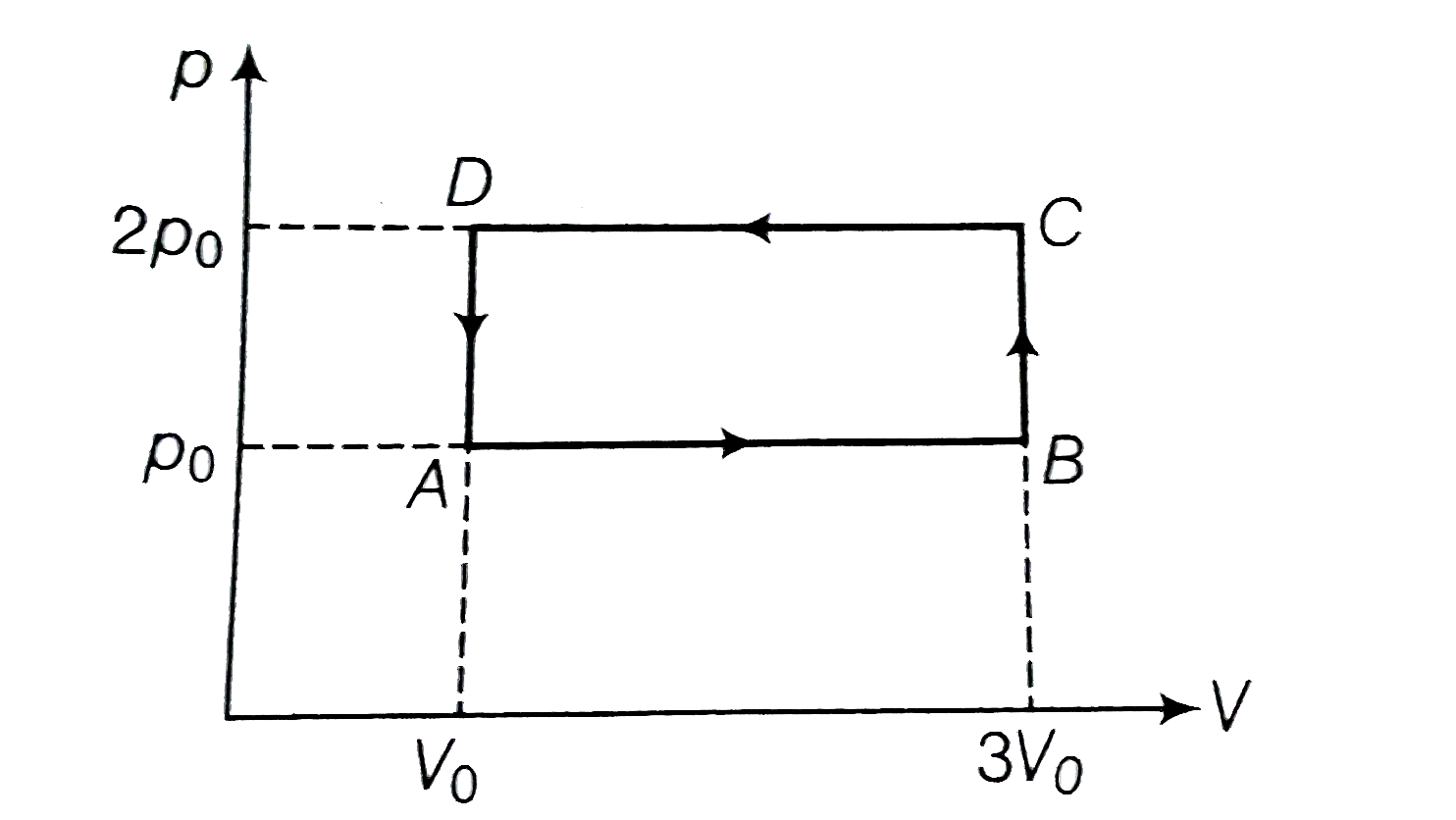
Work done =change in pressure × change in volume =(2P0−P0)(3V0−V0)=2P0V0)
since the cyclic process is anticlockwiese work done by the gas is negative i.e −2P0V0.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Assertion And Reason
15 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Higher Order Thinking Skills
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTIPSCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
An ideal gas undergoes cyclic process ACBC as shown is given PV diagram
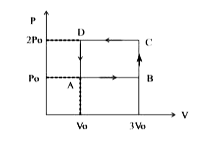
The amount of work done by the gas isA6PoVoB−2PoVoC+2PoVoD+4PoVoAn ideal gas underoges cyclic process of ABCDA as shown in Given P−V diagram (figure)
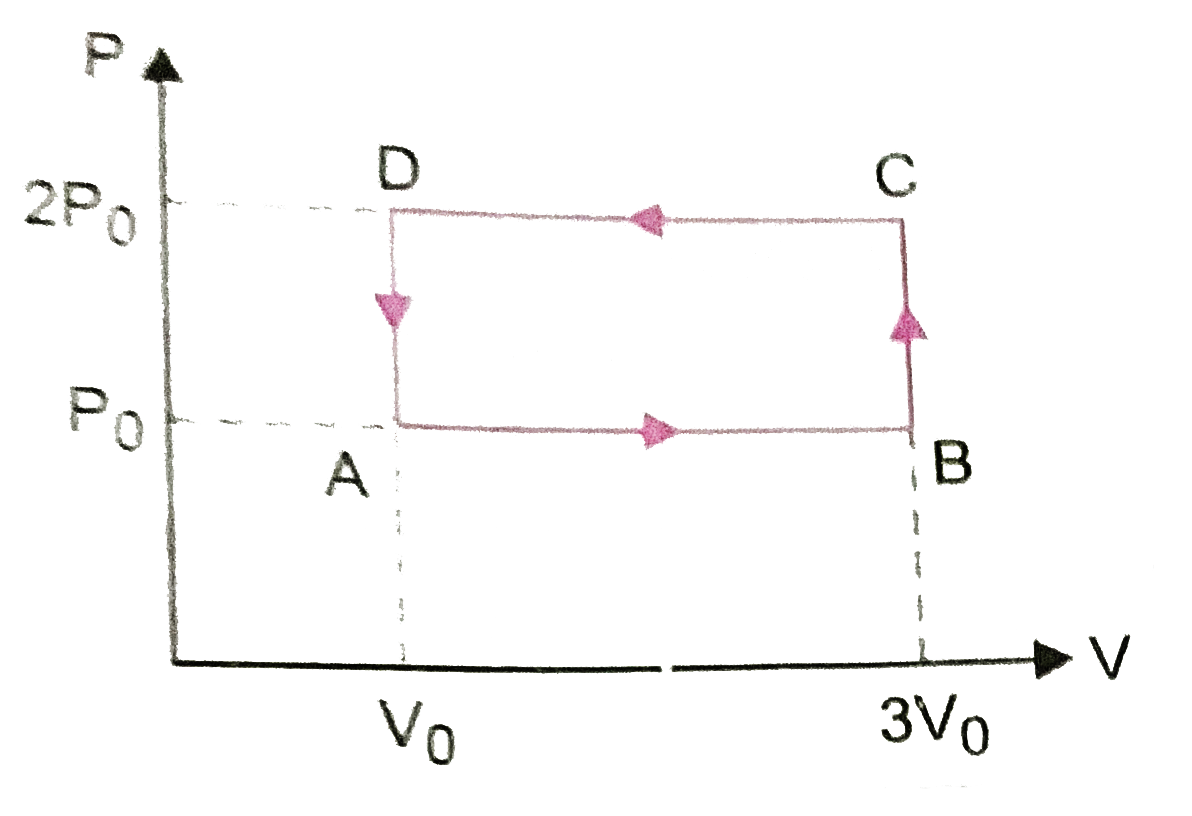
The amount of work done by the gas isA6P0V0B−2P0V0C+2P0V0D+4P0V0One mole of an ideal gas undergoes a cyclic process ABCDA as shown in the P-V diagram, The net work done in the process is
(1atm=106 dyne cm−2) A500 JB700 JC800 JD900 J
A500 JB700 JC800 JD900 J
An ideal gas undergoes the cyclic process shown in a graph below :
View SolutionOne mole of an ideal gas has an interal energy given by U=U0+2PV , where P is the pressure and V the volume of the gas. U0 is a constant. This gas undergoes the quasi− static cyclic process ABCD as shown in the U−V diagram.

The work done by the ideal gas in the process AB is
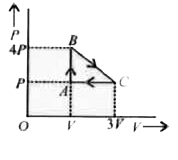
View SolutionAn ideal gas is taken around the cycle ABCA as shown in the P-V diagram.
The total work done by the gas during the cycle is
View SolutionAn ideal gas is taken around the cycle ABCA as shown in P-V diagram. The net work done by the gas during the cycle is equal to :
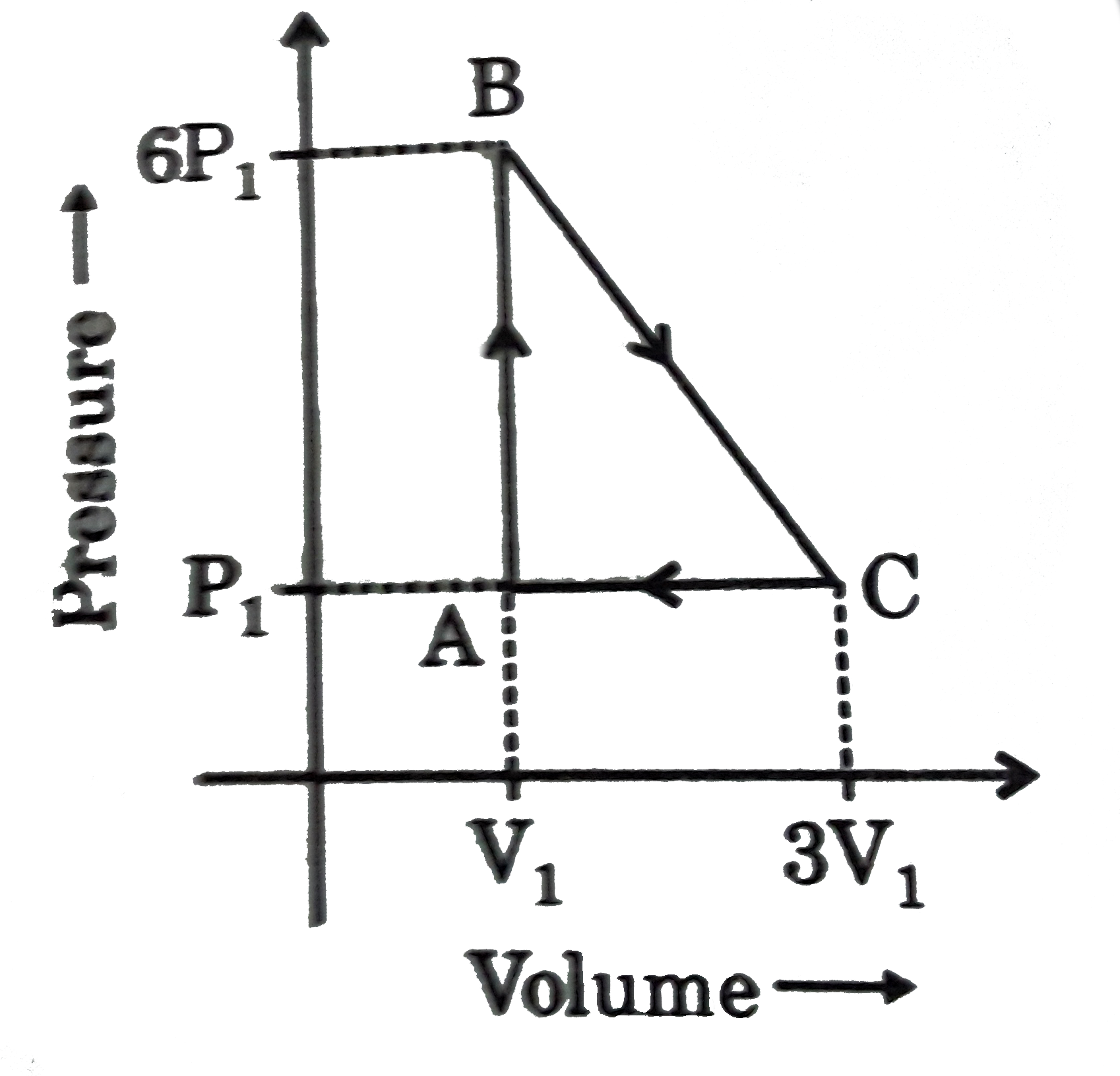
View SolutionAn ideal gas is taken around the cycle ABCA as shown in P−V diagram. The net work done by the gas during the cycle is equal to:
View Solution