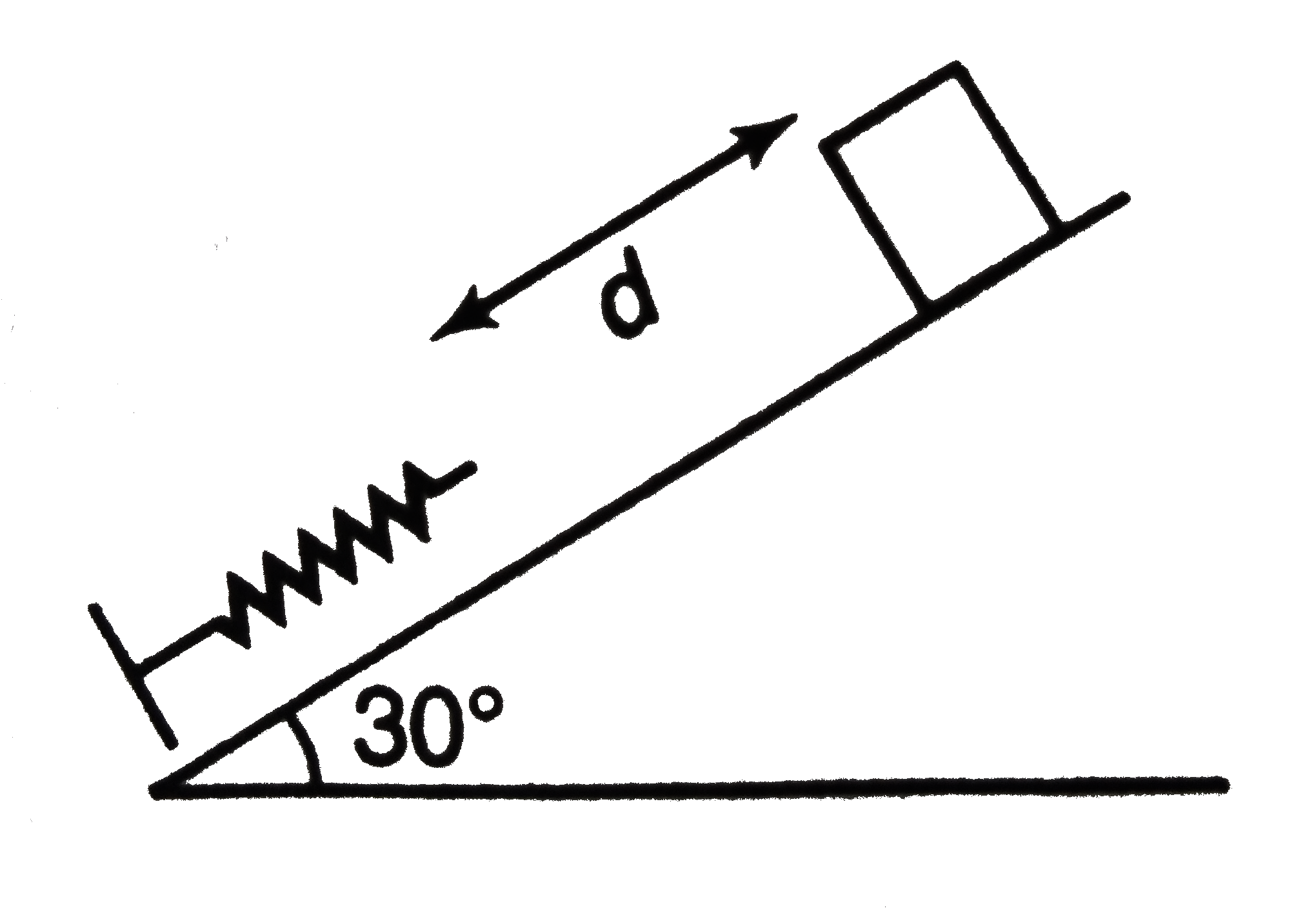
An ideal massless spring S can compressed 1.0 m in equilibrium by a force of 1000N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A 10kg mass m is released from the rest at top of the inclined plane and is brought to rest momentarily after compressing the spring by 2.0m. the distance through which the mass moved before coming to rest is.
8m
6m
4m
5m
The correct Answer is:C
From F=kx
k=Fx=1001.0
Decrease in gravitational potential energy =∈crease∈spr∈gpotentiale≠rgy<br>rArr 10 xx 10 xx (d + 2) sin 30^(@) =1/2 xx 100 xx (2)^(2)<br>Solv∈g,wedistancecoveredbeforecomingmomentarily→rest<br>= d + 2 = 4m.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion and Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
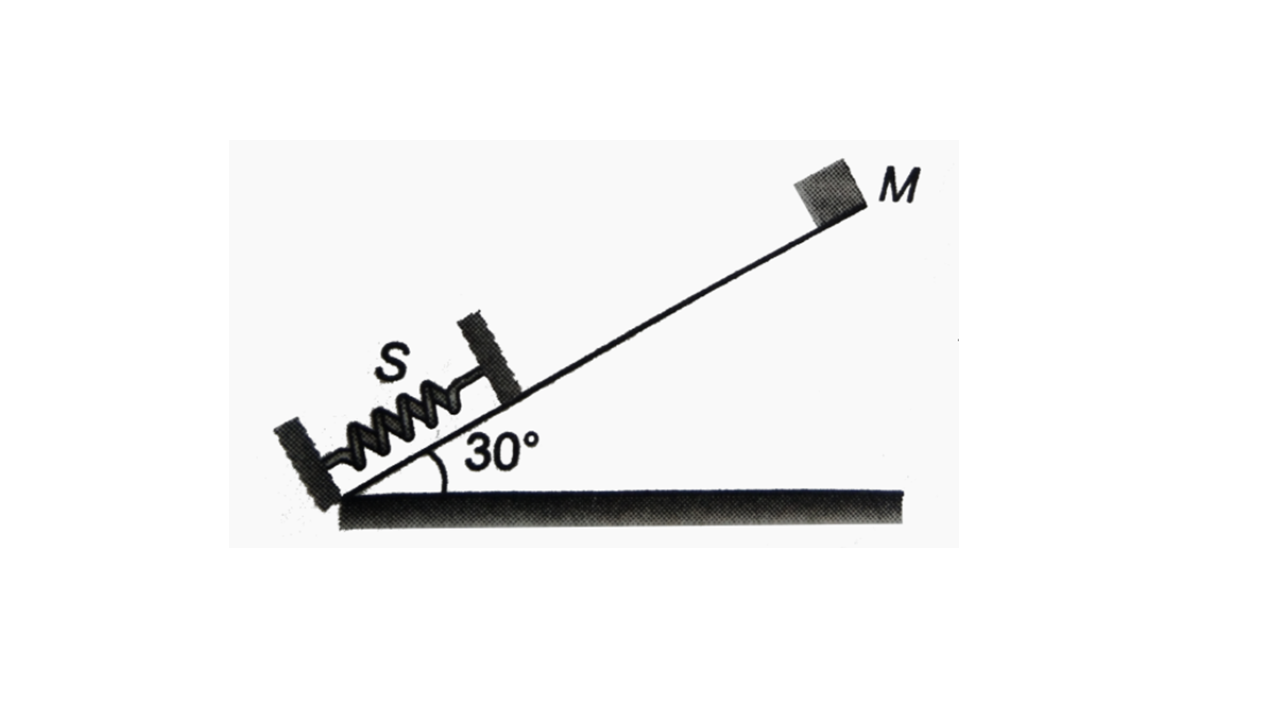
An ideal massless spring is compressed by 1 m by a force of 100 N. The same spring is placed at the bottom of a frictionless inclined plane (θ=30∘). A 10-kg mass is released from the top of the incline and is brought to rest momentarily after compressing the spring by 2m. Through what distance does the mass slide before coming to rest ?
[Hint : Apply work-energy theorem]
View SolutionAn ideal massles spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless plane inclined at 30∘ to the horizontal. A 10 kg block M is released from rest at the top of the incline and is brought to rest momentarily after compressing the spring by 2 m. If g=10m/s2, the speed of mass just before it touches the spring is √10xm/s. Find value of x?

View Solution
Knowledge Check
An ideal massless spring S can compressed 1.0 m in equilibrium by a force of 1000N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A (10 kg) mass (m) is released from rest at the top of the incline and and is brought to rest momentarily after compressing the spring by 2m. If g=10ms−1, what is the speed of just before it touches the spring?
 .A√20ms−1B√30ms−1C√10ms−1D√40ms−1
.A√20ms−1B√30ms−1C√10ms−1D√40ms−1When a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/mB100 N/mC150 N/mD200 N/mA body of mass 10kg is placed on a smooth inclined plane making an angle of 30∘ with the horizontal, the component of the force of gravity trying to move the body down the inclined plane is [g=9.8m/s2]
A98 NB49 NC10 ND5 N
A block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100M/m and block comes to rest after compressiong spring by 1 m, find the distance travelled by the block before it comes t o rest.

View SolutionAn inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution
