An ideal monatounic gas of mass $M$ is taken through a cyclic process $A B C$ . The process $A B$ is $P_{p} =$ constant. Totál work done by the gas in the process is $- \frac{α}{β} M \frac{P_{0}}{P_{0}} .$ Find $(α + β) .$
'(##CEN_KSR_PHY_JEE_C15_E01_018_Q11##)'

Text Solution

Verified by Experts

The correct Answer is:5

Updated on:21/07/2023

|

Class 12 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - QUESTION BANK
37 Videos

Similar Questions

Knowledge Check

One mole of an ideal diatomic gas is taken through a process whose $P - V$ diagram is shown in the figure. The work done by the gas is

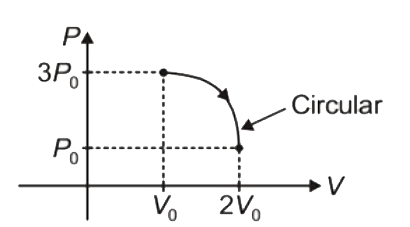A $π P_{0} V_{0} + 2 P_{0} V_{0}$
B $\frac{π P_{0} V_{0}}{2} + P_{0} V_{0}$
C $2 π P_{0} V_{0} + P_{0} V_{0}$
D $\frac{π P_{0} V_{0}}{\sqrt{2}} + P_{0} V_{0}$
An ideal gas undergoes cyclic process $A B C D A$ as shown in givend $p - V$ diagram. The amount of work done by the gas is

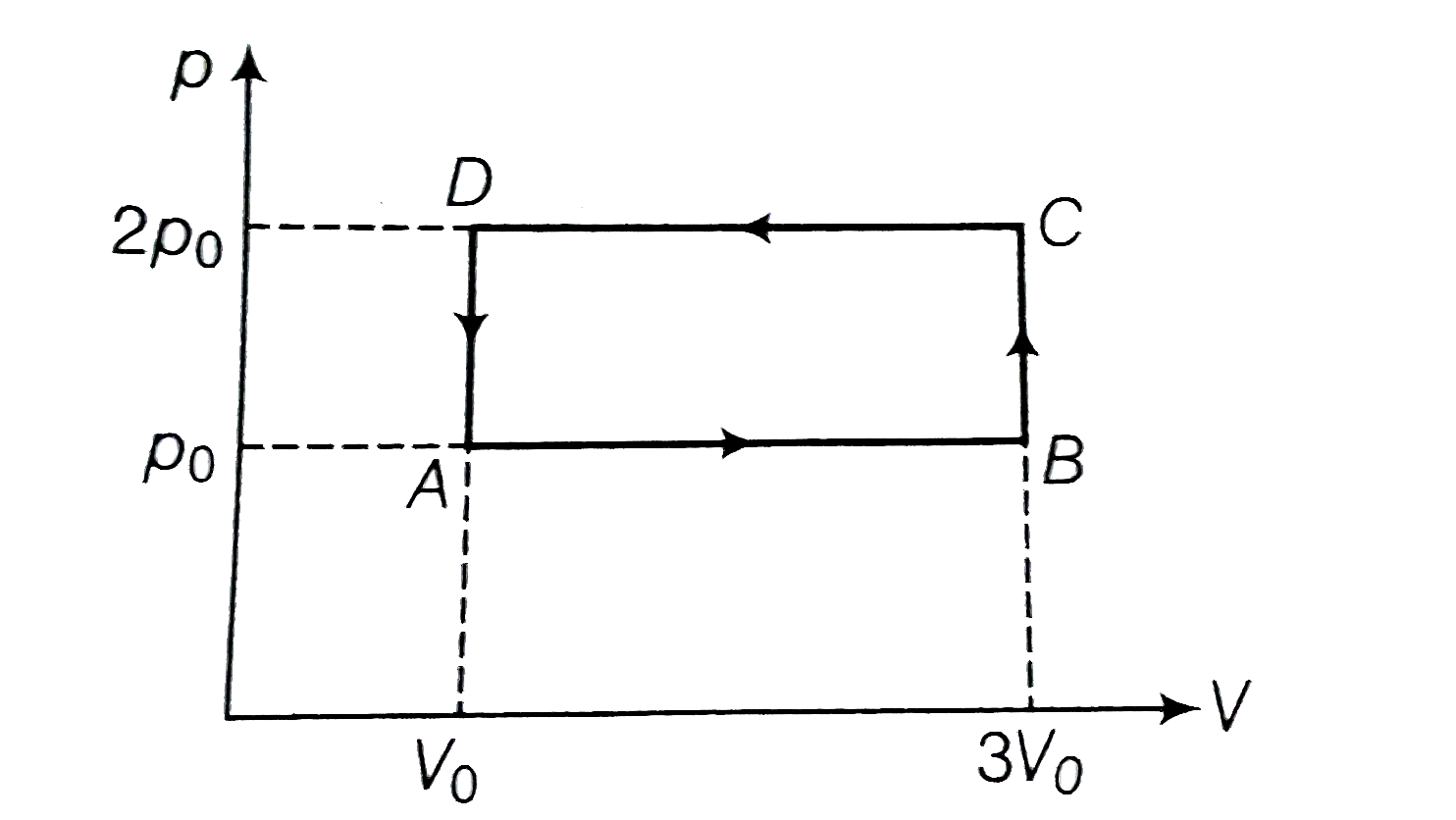A $6 p_{0} V_{0}$
B $- 2 p_{0} V_{0}$
C $+ 2 p_{0} V_{0}$
D $+ 4 p_{0} V_{0}$
An ideal gas undergoes cyclic process $A B C D A$ as shown in given $p - V$ diagram. The amount of work done by the gas is

A $6 P_{0} V_{0}$
B $- 2 P_{0} V_{0}$
C $+ 2 P_{0} V_{0}$
D $+ 4 P_{0} V_{0}$

CENGAGE PHYSICS-THERMODYNAMICS-QUESTION BANK

Home
Ask Doubt
Profile