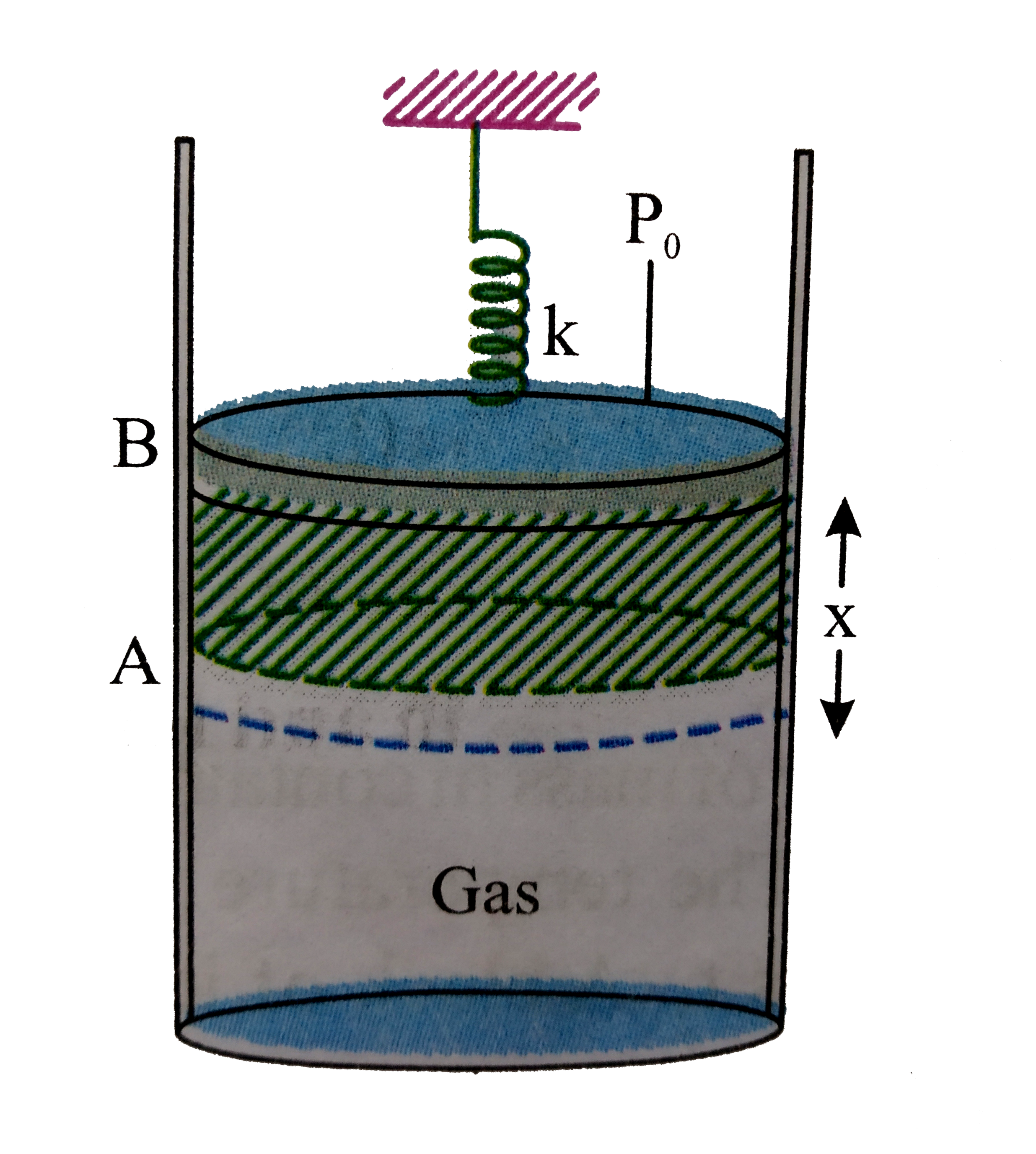
An ideal monoatomic gas is confined in a cylinder by a spring loaded piston of cross-section $8 \times 10^{- 3} m^{2}$ . Initially the gas is at 300K and occupies a volume of $2.4 \times 10^{- 3} m^{3}$ and the spring is in its relaxed (unstretched, uncompressed) state(see figure- 3.27). The gas is heated by a small electric heater until the piston moves out slowly by 0.1 m. Calculate the final temperature of the gas and the heat supplied (injoule) by the heater. The force constant of the spring is 8000 N/m, atmospheric pressure is $1 \times 10^{5} N / m^{2}$ . The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat-loss through the lead wires of the heater.The heat-capacity of the heater coilis negligible.Assume the spring to be massless.

Text Solution

Verified by Experts

Initially, the pressure of the gas in the cylinder is atmospheric pressure as spring is in relaxed state. Therefore
$P_{1}$ =atmospheric pressure $= 1.0 \times 10^{5} N / m^{2}$
$V_{1}$ = initial volume = $2.4 \times 10^{3} m^{3}$
$T_{1}$ =initial temperature =300 K
When heat is supplied by the heater,the piston is compressed by 0.1m.The reaction force of compression of spring is equal to k x which acts on the piston or on the gas as
F=kx=8000 x 0.1 = 800 Nt
Pressure exerted on the piston by the spring
$Δ P = \frac{F}{A} = \frac{800}{8 \times 10^{- 3}} = 1 \times 10^{5} N / m^{2}$
The total pressure $P_{2}$ of the gas inside cylinder is
$P_{2} = P_{a t m} + Δ P = 1 \times 10^{5} + 1 \times 10^{5}$
$= 2 \times 10^{5} N / m^{2}$
Since the piston has moved outwards, there has been an increase $Δ V$ in the volume of the gas
$Δ V = A \times x = (8 \times 10^{- 3}) \times (0.1)$
$= 8 \times 10^{- 4} m^{3}$
The final volume of the gas
$V_{2} = V_{1} + Δ V = 2.4 \times 10^{- 3} + 8 \times 10^{- 4}$
$= 3.2 \times 10^{- 3} m^{3}$
Let $T_{2}$ be the final temperature of gas. Then
$\frac{P_{1} V_{1}}{T_{1}} = \frac{P_{2} V_{2}}{T_{2}}$
or $T_{2} = T_{1} \frac{P_{2} V_{2}}{P_{1} V_{1}}$
$= 300 \times \frac{2 \times 10^{5} \times 3.2 \times 10^{- 3}}{10^{5} \times 2.4 \times 10^{- 3}}$
=800 K
Let the heat supplied by the heater be Q. This is used in two parts: a part is used in doing external work W due to expansion of the gas and the other part is used in increasing the internal energy of the gas. Hence
$Q = W + Δ U$
Now $W = \int_{V_{1}}^{V_{2}} P d V = \int_{0}^{x} (P_{a t m} + \frac{k x}{A}) A d x$ [As pressure is $(P_{a t m} + k x / A)$ and dV=A dx ]
or $W = P_{a t m} A x + \frac{k x^{2}}{2}$
$= [10^{5} \times (8 \times 10^{- 3}) (0.1) + \frac{8000 \times {(0.1)}^{2}}{2}]$
=120 joule
Further $U = n C_{v} Δ T$
Number of moles of gas can be obtained from initial conditions and gas law as
$n = \frac{P V}{R T} = \frac{1 \times 10^{5} \times 2.4 \times 10^{- 3}}{8.314 \times 300}$
=0.096 mole
Thus change in internal energy of gas is given as
$Δ U = n (\frac{3}{2} R) Δ T$ [ As for monoatomic gas $C_{V} = \frac{3}{2} R$ ]
or $U = 0.096 \times \frac{3}{2} \times 8.314 \times 500$ =598.6 Joule
Heat supplied by heater
=120+598.6)
=718.6 joule

Updated on:21/07/2023