An illuminant shaped as a plane horizontal disc of raiud R=25cm is suspended over a table at a hight h=75cm. The illuminance of the table below the cnetre of the illuminant is equal to E0=70Ix. Assuming the source to obey Lambert's law, find its luminosity.
Consider an angular element of area
2πxdx=2πh2tanθsec2θdθ
Light emitted from his ring is
dΦ=LdΩ(2πh2tanθsec2θdθ).Cosθ
Now dΩ=dAcosθh2sec2θ
where dA= an element of area of the table just below the untre of the illuminant. Then the illuminance at the element dA will be
E0=∫θ−αθ−02πLsinθcosθdθ
where sinα=R√h2+R2. Finally using luminosity M=πL
E0=Msin2α=MR2h2+R2
or M=E0(1+h2R2)=7001m/m2⋅(11x=11mm2 dimensionally).

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light33videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light60videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems92videos
MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
Similar Questions
An illuminant shaped as a plane horizontal disc S=100cm2 in area is suspended over the centre of a round table of radius R=1.0m. Its luminance does not depend on direction and is equal illuminant be suspended to provide maximum illuminance at the circumference of the table ? How great will that illuminance be? The liuminant is assumed to be a point source.
View SolutionFigure shows a small diffused plane source S placed over a horizontal table-top at a distance of 2.4 m with its plane parallel to the table-top. The illuminance at the point A directly below the source is 25 lux. Find the illuminance at a point B of the table at a distance of 1.8 m from A.
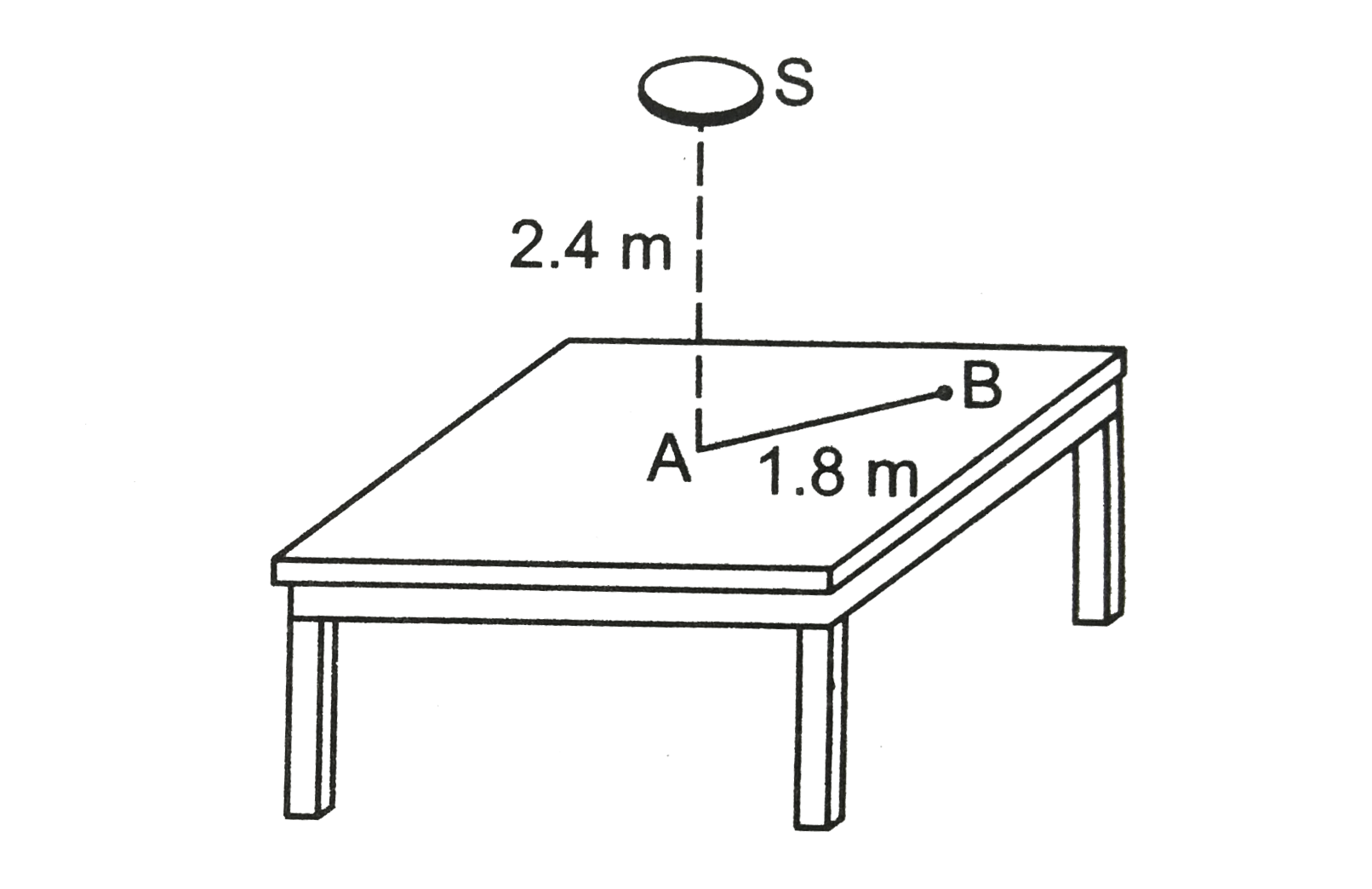 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A point source of light moves ijn a straight line paralel to a plane table. Consider a small portion of the table directly below the line of movement of the source. The illuminance at this portion varies with its distasnce r from the source as
AI∝1rBI∝1r2CI∝1r3DI∝1r4 - Question 2 - Select One
A point source of light moves in a straight line parallel to a plane table. Consider a small portion of the table directly below the line of movement of the source. The illuminance at this portion varies with its distance r from the source as
AE∝1rBE∝1r2CE∝1r3DE∝1r4
A small lamp having the from of a unifromly sphere of radius R=6 cm is suspended at a height h=3m above the floor. The luminance of the lampis equal to L=2×104cd/m2. Find the illuminance of the floor below the lamp.
(Hint:P=∑LΔScosθ=L×πR2)View SolutionA small lamp having the form of a unfromly luminous sphere of radius R=60cm is suspended at a height h=3.0m above the floor. The luminance o fthe lamp is equal to L=2.0.104cd/m2 and is independent of direction. Find the illuminance of the floor directly below the lamp.
View SolutionA point source emitting light uniformly in all directions is placed 60 cm above a table-top. The illuminance at a point on the table-top, directly below the source, is 15 lux. Find the illuminance at a point on the table-top 80 cm away from the first point.
View SolutionA vertical shaft of light from a projector forms a light spot S=100cm2 in area on the celling of a round room of radius R=2.0m. The illuminance of the spot is equal to E=10001x. The reflection coeffiecient of the celling is equal to ρ=0.80. find the maximum illuminance of the well produced by the light reflected from the celling. the reflection is assumed to obey Lambert's law.
View Solution_E01_234_Q01.png)
A thin horizontal disc of radius R=10cm is located with in a cylindrical cavity filled with oil whose viscosity η=0.08P (figure) The distance between the disc and the horizontal planes of the cavity is equal to h=1.0 mm find the power developed by the viscous forces acting ont he disc when it rotates with the angular velocity ω=60rad/s. The end effect are to be neglected.View SolutionA point source is suspended at a hight h=1.0m over the centre of a round table of radius R=1.0m. The luminous intensity I of the source depends on direction so that illuminance at all points of the table is the same. Find the function I(θ), where θ is the angle between the radiation direction and the vertical, as well as the luminous flux reaching the table if I(0)=I0=100cd.
View Solution

