An inclined plane is bent in such a way that the vertical cross-section is given by y=x24 where y is in vertical and x in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction μ = 0.5, the maximum height in cm at which a stationary block will not slip downward is______cm.
The correct Answer is:25
To solve the problem, we need to determine the maximum height at which a stationary block will not slip down an inclined plane defined by the equation y=x24. Given that the coefficient of friction μ=0.5, we will follow these steps:
Step 1: Understand the Geometry of the Inclined Plane
The equation y=x24 describes a parabola that opens upwards. The height y at any horizontal distance x is given by this equation.
Step 2: Find the Slope of the Inclined Plane
To find the slope of the inclined plane at any point, we need to differentiate the equation with respect to x:
dydx=ddx(x24)=2x4=x2
Step 3: Determine the Angle of Inclination
The slope dydx gives us tanθ, where θ is the angle of inclination of the plane:
tanθ=x2
Step 4: Apply the Condition for No Slipping
For the block to remain stationary, the angle of inclination must satisfy the condition:
tanθ=μ
Given μ=0.5, we have:
tanθ=0.5
Step 5: Set the Two Expressions for tanθ Equal
Now, we equate the two expressions for tanθ:
x2=0.5
Step 6: Solve for x
Multiplying both sides by 2 gives:
x=1
Step 7: Substitute x Back to Find y
Now that we have x=1, we can substitute this value back into the equation for y:
y=x24=124=14
Step 8: Convert Height to Centimeters
Since the height y is in meters, we convert it to centimeters:
y=14 m=0.25 m=25 cm
Final Answer
The maximum height at which a stationary block will not slip downward is 25 cm.
---
The equation y=x24 describes a parabola that opens upwards. The height y at any horizontal distance x is given by this equation.
To find the slope of the inclined plane at any point, we need to differentiate the equation with respect to x:
The slope dydx gives us tanθ, where θ is the angle of inclination of the plane:
For the block to remain stationary, the angle of inclination must satisfy the condition:
Now, we equate the two expressions for tanθ:
Multiplying both sides by 2 gives:
Now that we have x=1, we can substitute this value back into the equation for y:
Since the height y is in meters, we convert it to centimeters:
The maximum height at which a stationary block will not slip downward is 25 cm.
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION-A)20videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION-B)10videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A80videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions473videos
JEE MAIN
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question492videos
JEE MAIN 2022
Similar Questions
A block of mass 'm' is placed on a rough surface with a vertical cross section of y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is .
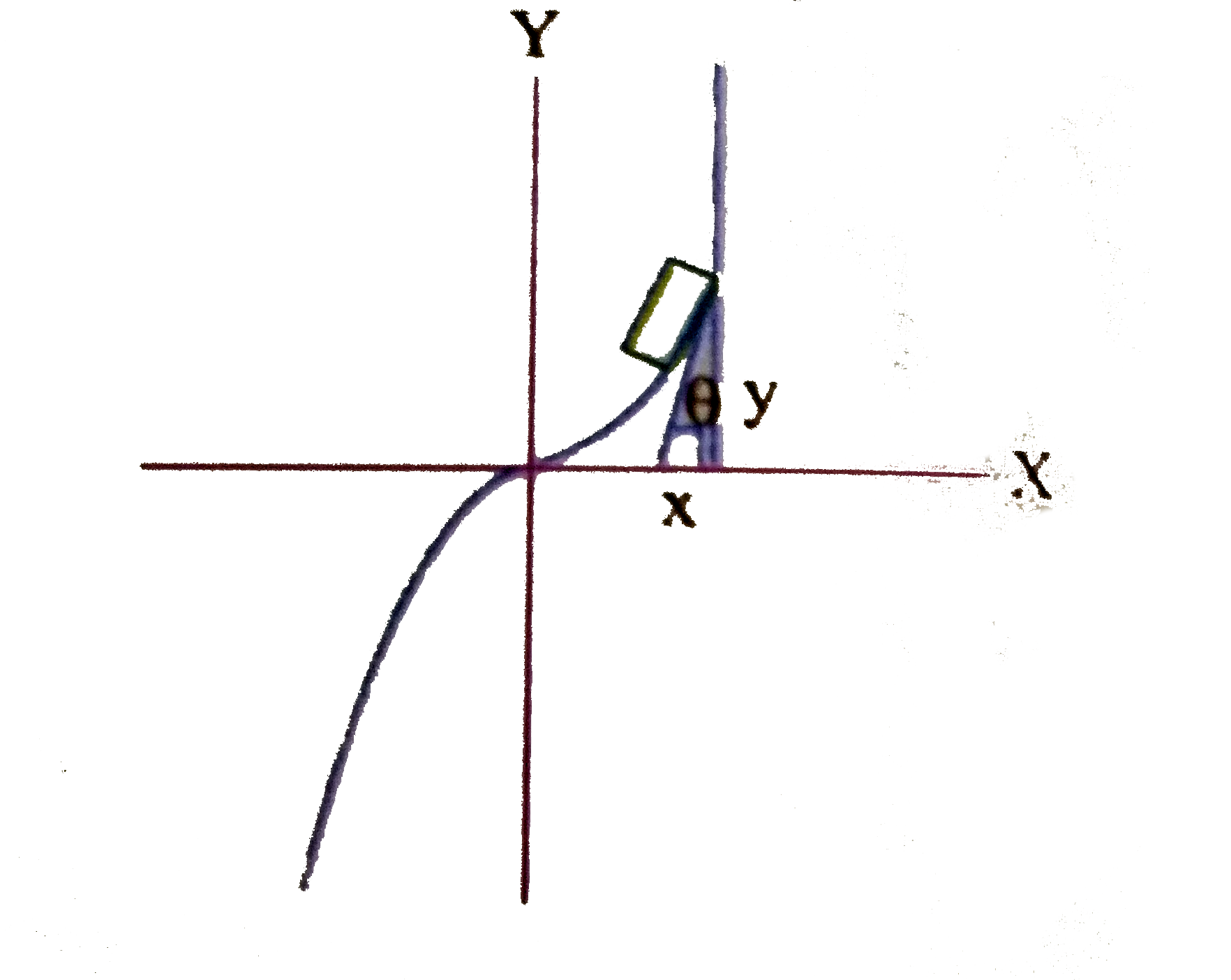 View Solution
View Solution
A small back starts slipping down from a point B on an inclined plane AB, which is making an angle θ with the remaining section CA is rough with a coefficient of friction μ. It is found that bottom (point A) of the inclined plane. If BC=2AC, the coefficient of friction is given by μ=Ktanθ
The value of K is ________.View Solution
Knowledge Check
- Question 1 - Select One
A block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
A(a) 16mB(b) 23mC(c) 13mD(d) 12m - Question 2 - Select One
A block of mass m is at rest on an incline having an angle of inclination θ with the horizontal. The incline is now being rotated with constant angular velocity ω about an axis passing through the perpendicular side. If the surface of the incline is rough having coefficient of friction as μ, then find the distance 'x' aong the incline so that block just remains stationary with restpect to incline and is on the verge of slipping. [ Take 'x' from the top of the incline as shown in the figure.]
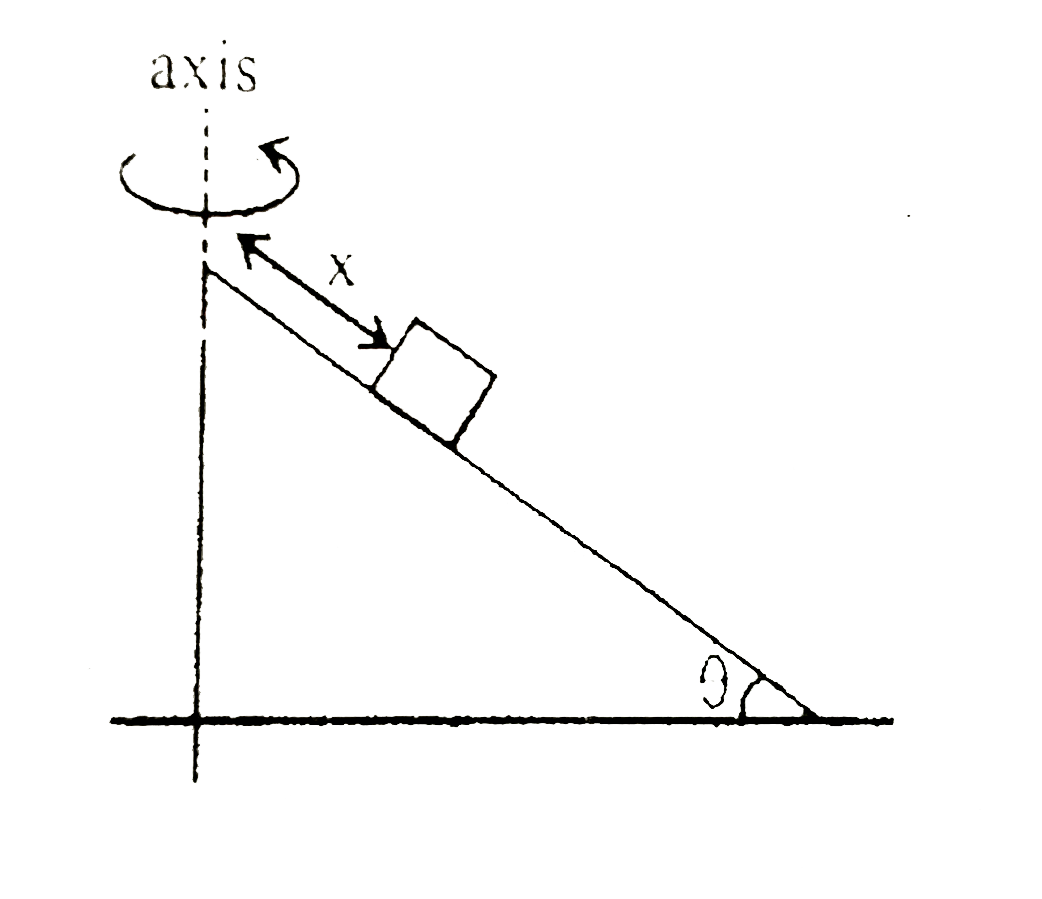 Agω2(μ+tanθ)(μtanθ−1)Bgω2(μ−tanθ)(μtanθ+1)Cgω2cosθ(μ−tanθ)(μtanθ+1)Dgω2(μ−tanθ)(μtanθ−1)
Agω2(μ+tanθ)(μtanθ−1)Bgω2(μ−tanθ)(μtanθ+1)Cgω2cosθ(μ−tanθ)(μtanθ+1)Dgω2(μ−tanθ)(μtanθ−1) - Question 3 - Select One
A small mass slides down an inclined plane of inclination θ the horizontal the coefficient of friction is m=μ0x, where x is the distance by the mass before it stops is .
A1μ0tanθB4μ0tanθC12μ0tanθD1μ0tanθ
A cannon of mass 1000kg located at the base of an inclined plane fires a shell of mass 50kg in horizontal direction with velocity 180km/h. The angle of inclination of the inclined plane with the horizontal is 45∘. The coefficient of friction between the cannon and inclined plane is 0.5. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
View SolutionA cannon of mass 2m located at the base of an inclined plane shoots a shell of mass m in horizontal direction with velocity v0 The angle of inclination of plane is 45∘ and the coefficient of friction between the cannon and the plane is 0.5 The height to which cannon ascends the plane as a result of recoil is :
View SolutionThe trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
View SolutionThe trajectory of a projectile in a vertical plane is y=ax−bx2, where a and b are constants and x and y are respectively horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projection form the horizontal are:
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
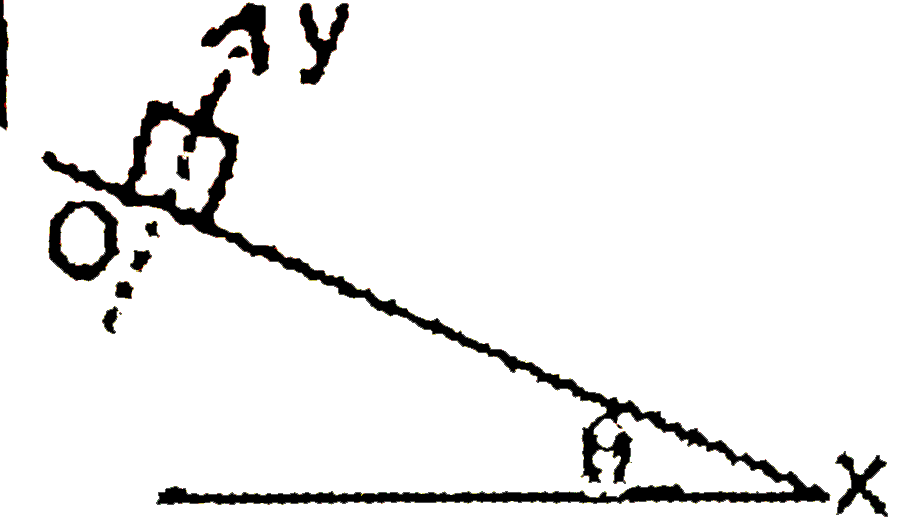
The maximum velocity of block will be :View Solution

