An inductance L and a resistance R are first connected to a battery. After some time the battery is disconnected but L and R remain connected in a closed circuit. Then the current reduces to 37% of its initial value in
R/L
R/L
L/R
1/LR
The correct Answer is:C
i0=E/R
i=i1e−RtL
0.37i0=i0e−RtL
e−RtL=10.37=2.7
RtL=1n(2.7)⇒RtL=1⇒t=LR
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
An inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
Aε4RBε2RC2RεD4Rε - Question 2 - Select One
An inductance L and a resistance R are connected in series with a battery of emf ε. The maximum rate at which the energy is stored in the magnetic field is :
Aε4RBε2RC2RεD4Rε - Question 3 - Select One
A coil resistance R and inductance L is connected to a battery of emf E volt. The final current in the coil is
AERBELC√(ER2+L2)D√(ELR2+L2)
A coil having an inductance L and a resistance R is connected to a battery of emf E . Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value.
View SolutionA coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before (a) the current reaches half its maximum value, (b) the power dissipated in heat reaches half its maximum value and © the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionThe current in an L - R circuit in a time t = 2L / R reduces to-
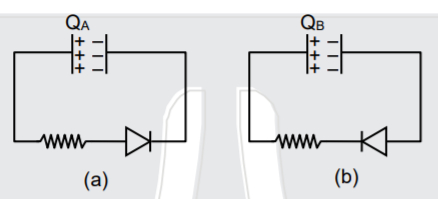
View SolutionA Capacitor C and resister R are connected to a battery of 5V in series. Now battery is disconnected and a diode is connected as shown in figure (a) and (b) respectively. Then charge on the capacitor after time RC in (a) and (b) respectively is QA and QB. Their value are
 View Solution
View SolutionAn inductor L and a resistance R are connected in series with a battery of emf E and a switch. Initially the switch is open. The switch is closed at an instant t = 0. Select the correct alternatives
View Solution

