An infinite carrying conductor is bent into three segment (1), (2) and (3) as shown in Fig. If it carries a current i, find the magnetic induction at the origin.
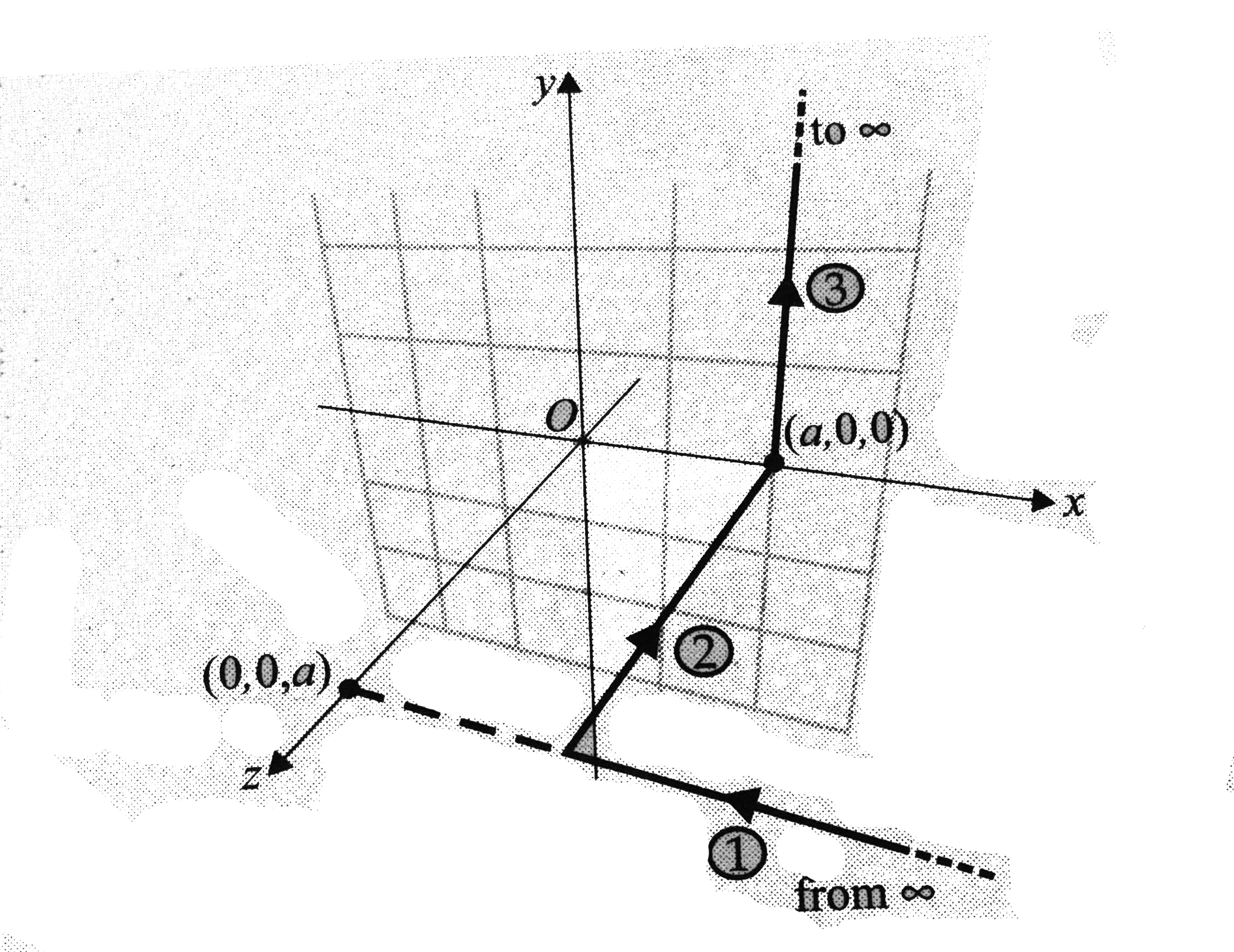
Net magnetic field at O will be the vector sum of magnetic
fields due to wires (1) , (2) and (3).
Magnetic field due to wire (1),
→B1=μ04πIa[sin90∘−sin45∘](−ˆj)
=μ04πia[1−1√2](−ˆj)
Magnetic field due to wire (2),
→B2=μ04πIa[sin45∘−sin0∘](ˆj)
=μ04πia[1√2](ˆj)
Magnetic field due to wire (3),
→B3=μ04πIa(ˆk)
Hence, net magnetic field →B=→B1+→B2+→B3
⇒μ04πia[(√2−1)ˆj+ˆk]
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
An infinite current carrying conductor is bent into three segments as shown in the figure-4.228. if it carries current i, the m agnetic field at the origin is found to be μolrπa(√x−1ˆj+ˆk). The value of x is:
 View Solution
View SolutionThe segment of wire shown in figure carries a current of i=5 A. The magnetic field (in Tesla) at the point P is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Shown in the figure is a conductor carrying a current i. the magnetic field at the origin is :
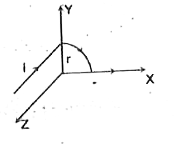 Aμ0i4r(ˆiπ+ˆj2)B−μ0i4r(ˆiπ+ˆk2)Cμ0i4r(ˆi2+ˆiπ)Dμ0i4r(2ˆiπ+ˆj)
Aμ0i4r(ˆiπ+ˆj2)B−μ0i4r(ˆiπ+ˆk2)Cμ0i4r(ˆi2+ˆiπ)Dμ0i4r(2ˆiπ+ˆj) - Question 2 - Select One
An infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R meter. The magnetic induction at the centre of loop is
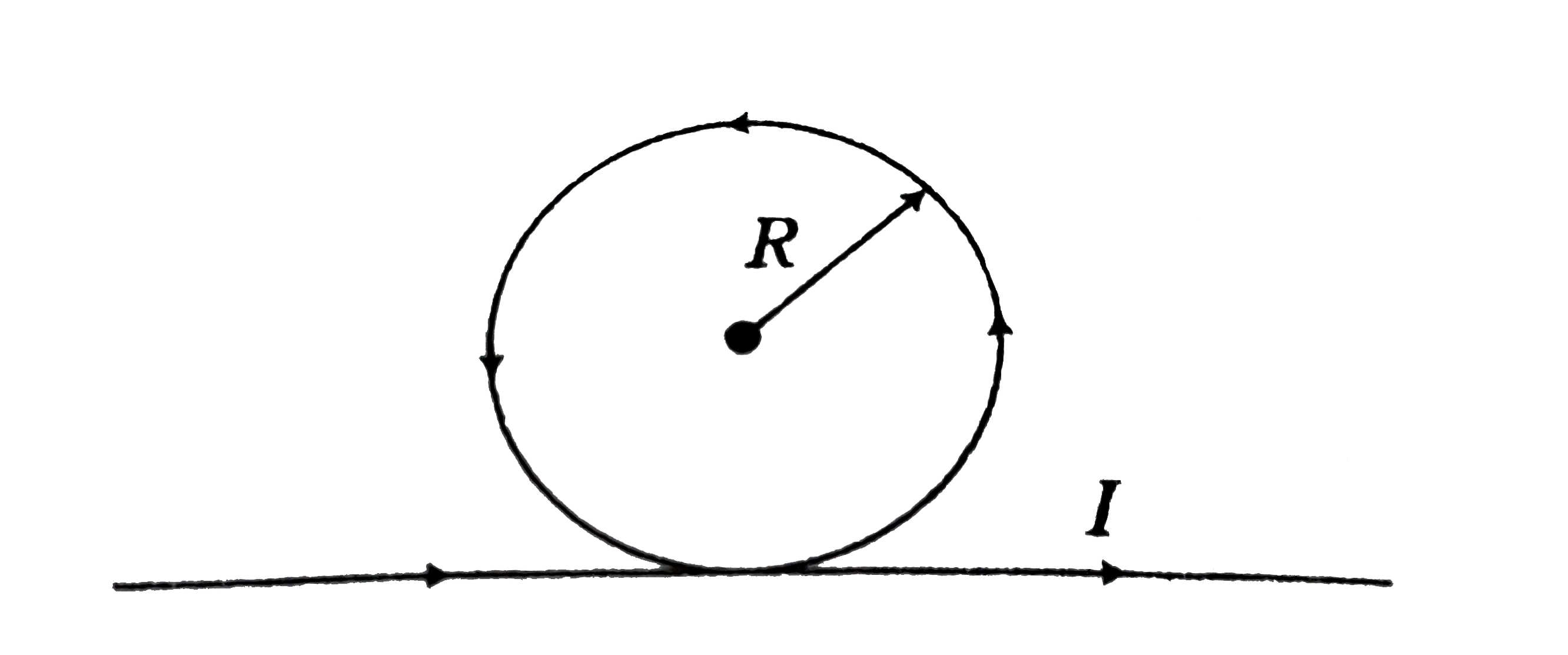 Aμ02I4πR(π+1)Bμ02I4πR(π−1)Cμ0I8πR(π+1)Dzero
Aμ02I4πR(π+1)Bμ02I4πR(π−1)Cμ0I8πR(π+1)Dzero - Question 3 - Select One
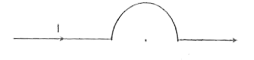
An infinitely long straight conductor is bent into the shape as shown in the figure. It carries a current of i ampere and the radius of the circular loop is V metre. The magnetic induction at the centre of the circular part is-
 Aμ0I4π(π−1)Bμ0i2a(1−1π)Cμ0i2a(π−1)Dμ0i4a(1−1π)
Aμ0I4π(π−1)Bμ0i2a(1−1π)Cμ0i2a(π−1)Dμ0i4a(1−1π)
An infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
 View Solution
View SolutionShown in Fig. is a conductor carrying current I. Find the magnetic field intensity at point O.
View SolutionA wire of infinite length bent as shown in figure carries current l. What is the magnetic field at the point P ?
 View Solution
View SolutionAn infinitely long straight conduction is bent into the shape as shown in the figure . It carries a current of I ampere and the radius of the circular loop is r metre. Then the magnetic induction at its centre will be
 View Solution
View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is
 View Solution
View Solution

